【高阶数据结构】图详解第二篇：图的遍历（广度优先+深度优先）

图的遍历

所谓图的遍历：

即从图中的任一顶点出发，对图中的所有顶点访问一次且只访问一次。
给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶点仅被遍历一次。

ps：

我们后面讲解这些图相关的算法默认都针对邻接矩阵结构的图去讲解，因为后面有些算法针对的图一般都是比较稠密的图，前面我们说了邻接矩阵更适合稠密图。

那具体要如何对一个图进行遍历呢？有哪些方法呢？

1. 图的广度优先遍历（一石激起千层浪）

什么是广度优先遍历呢？

其实我们之前学过的二叉树的层序遍历就是一种广度优先遍历，要借助一个队列来搞，下面对图的广度优先遍历也是一样

思路分析

那图的广度优先遍历是怎么样的呢？举个栗子：

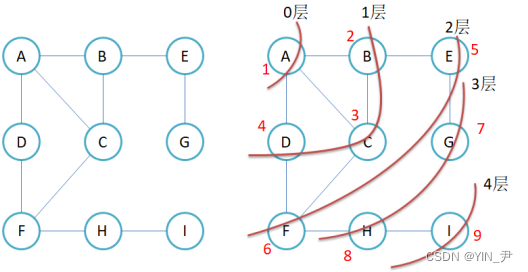
这就是对一个图（无向图）的广度优先遍历，红色的数字就是结点遍历的顺序。
大家看，其实就是一层一层的遍历嘛，这里是从A这个顶点开始，所以先遍历结点A，然后依次遍历与A直接相连的一层的结点，接着逐层向外扩展，直到遍历完所有可达的节点。

那我们用代码要怎么实现呢？

其实就跟二叉树的层序遍历类似，借助一个队列就可以搞定。
比如就以这个图为例：

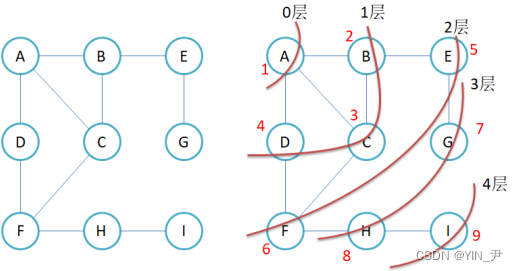
从顶点A开始，那就让A先入队列。

队列不为空，出队头元素A，然后我们打印一下A的值，那这个顶点就遍历过去了，然后把与A直接相连的顶点BCD入队列

队列不为空，继续出队头元素B，然后把与B直接相连的顶点入队列

那现在就出现了一个问题：

现在要把与B直接相连的顶点入队列，而与B直接相连的顶点是A、C、E。
但是，A前面已经遍历过了，C现在也在队列里面呢！
E入队列的话是没问题的，他就是下一层的，但是AC要是再入队列的话这就不对了啊。

那我们如何解决这个问题呢？如果避免某些顶点会重复入队列呢？

🆗，我们可以想办法对已经遍历过的结点做一个标记，这个即使后面再遇到，我们也能分辨出来，不让它再入队列了。

那如何标记已经遍历过的顶点呢？

每个顶点不是都映射一个下标嘛。
所以我们就可以开一个数组，默认都给false，遍历一个结点，就把对应下标位置的值改为true，表示这个结点已经被遍历过了。

那我们何时去标记一个顶点呢？打印之后标记还是入队列就标记呢？

如果打印之后标记的话，B出队列之后其实还会把C带到队列里面

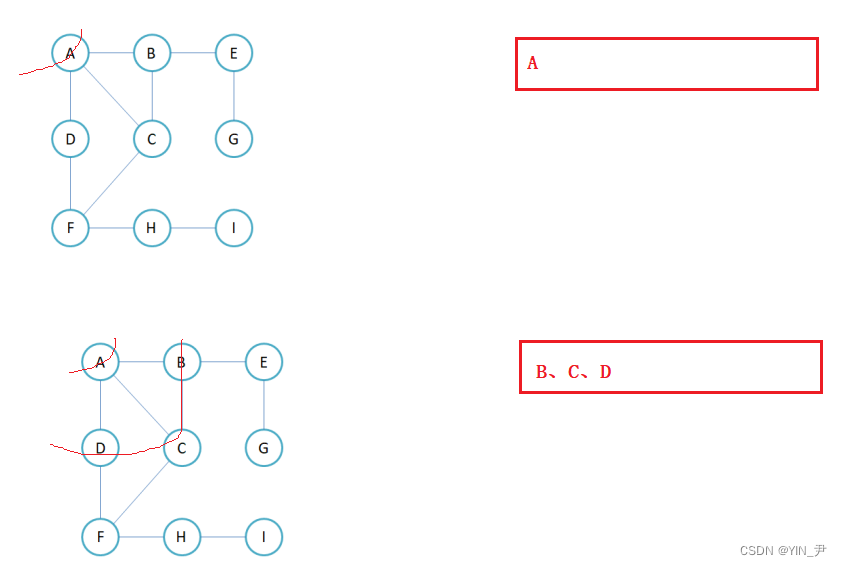
因为B出队列，然后打印B，此时A已经打印过了被标记了，但是C还没有出队列打印，所以C还没有被标记，所以B打印之后入与B直接相连的顶点ACE的时候，A不会入，但是C还会入。
不管也没关系，因为出到第二个C的时候，第一个C 肯定被标记了，那我们就可以判断，然后不打印第二个C，只把它出队列。

当然更好的做法是这样的：

一个顶点入队列的时候我们就去标记它，这样就不会出现上面的情况（队列里面出现重复顶点）

代码实现

那我们来写一下代码：

调用的时候给一个起始顶点就可以了
那我们需要一个队列和一个标记数组，首先起始顶点入队列

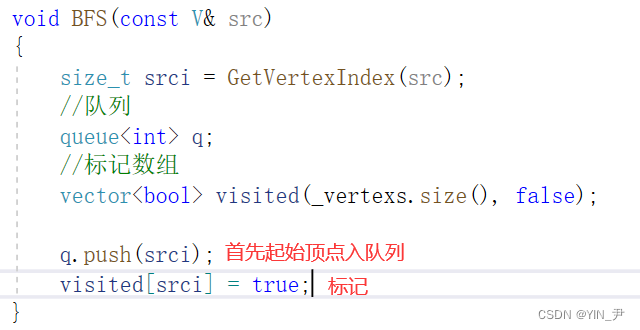
然后我们就按照上面的逻辑一层一层走就行了，循环出队列里面的元素并把与之直接相连的结点入队列，直到队列为空就是遍历完了，循环结束

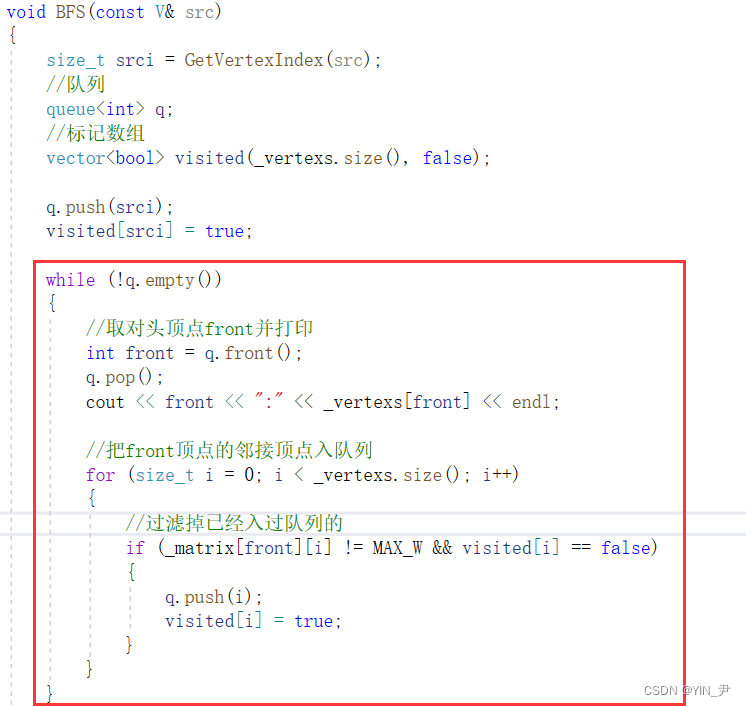
🆗，就写好了

测试

那我们来测试一下：

它对应的图应该是这样的

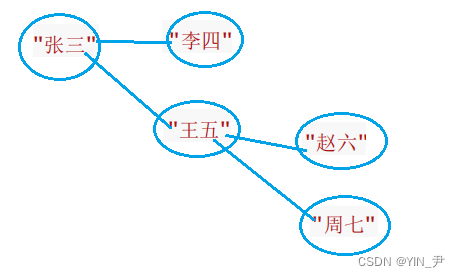
我们现在以张三为起点对其进行广度优先遍历

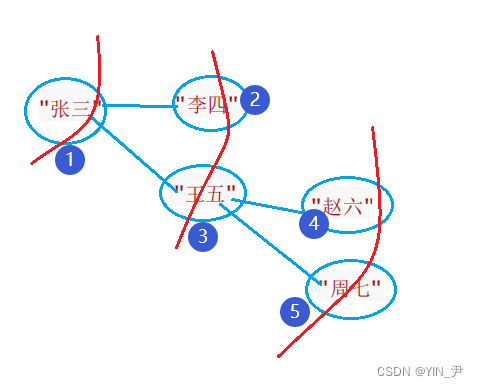
我们来看下结果对不对

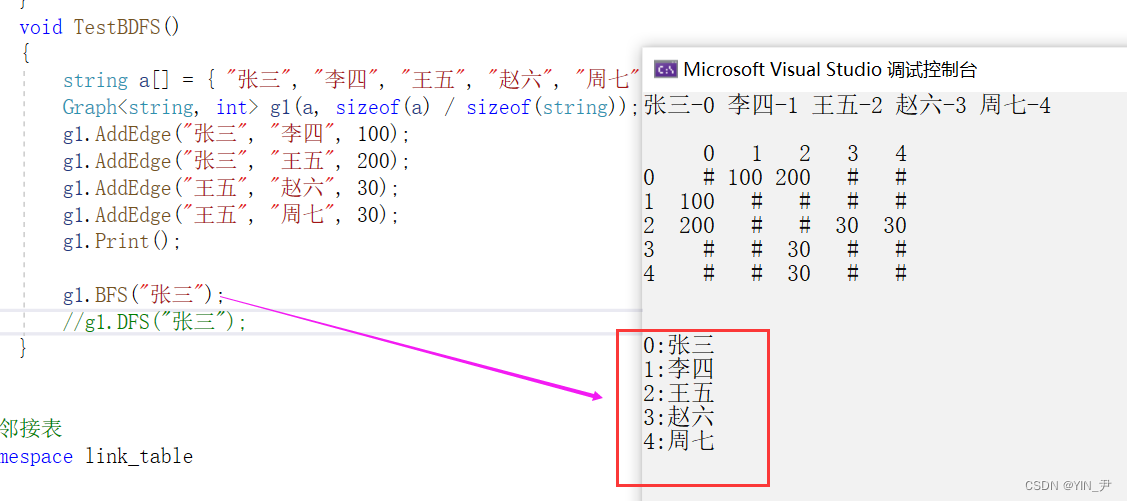
没问题

美团2020校招笔试题：六度人脉

然后我们来看一道美团曾经考过的一道问答题：
题目链接: link

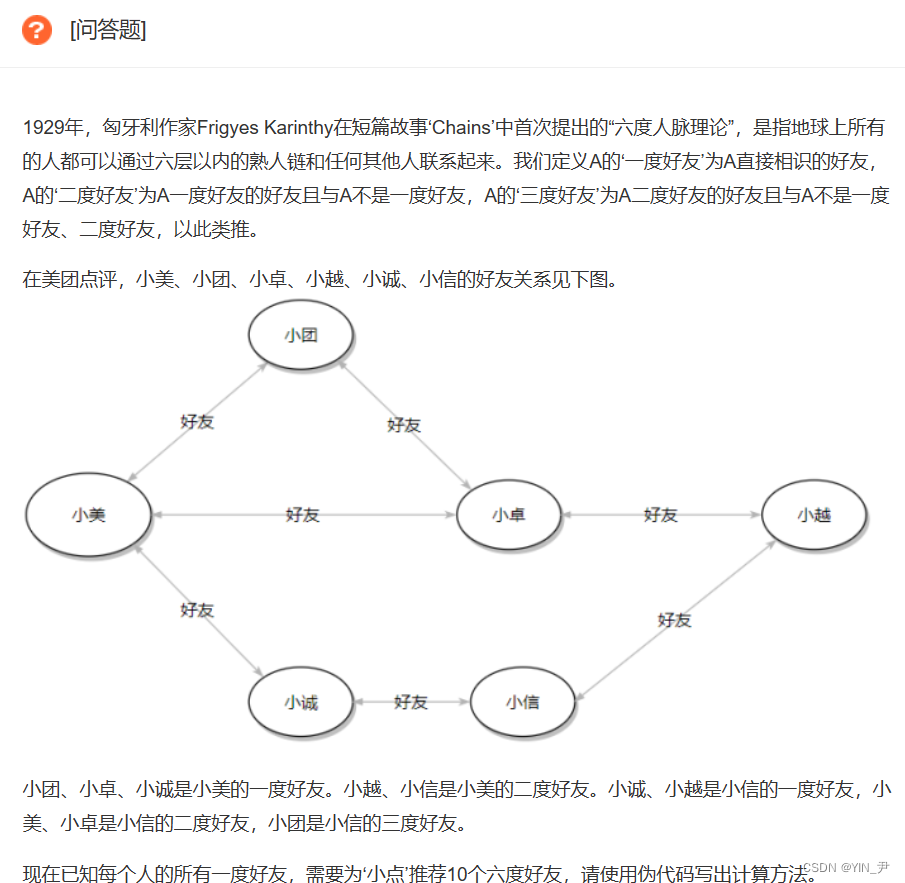
大家自己先读一下题

🆗，我们来分析一下：

这道题目最终的问题是让我们为小点推荐6度好友，如何找到哪些是它的6度好友呢？
其实很简单：
如果我们用上面实现的广度优先遍历去遍历对应的好友的关系图的话，我们一层一层的打印，第六层打印出来的人就是6度好友。

那我们上面实现的广度优先遍历打印的时候并没有分层打印，所以我们可以给上面的代码优化一下，让它分层打印就行了：

那如何做到分层打印呢？
其实这个问题我们之前也有遇到过，前面的文章里我们有讲过一个OJ题，也是二叉树的层序遍历，但是要求把每一层的结点都分开存放到一个数组里面，最终返回的就是一个二维数组嘛。
大家回想一下我们当时怎么做的？
🆗，增加一个变量，去记录每一层结点的个数，每出一个，就- -一次，一层出完，继续记录下一层的个数，这样就可以控制分层打印了。
那我们来把上面的代码改进一下

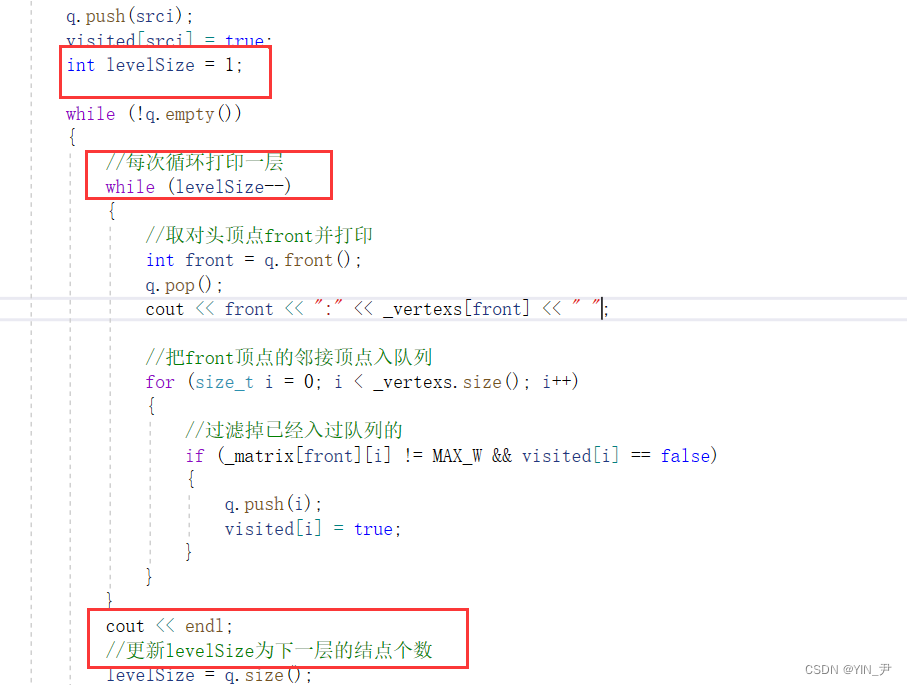
试一下：

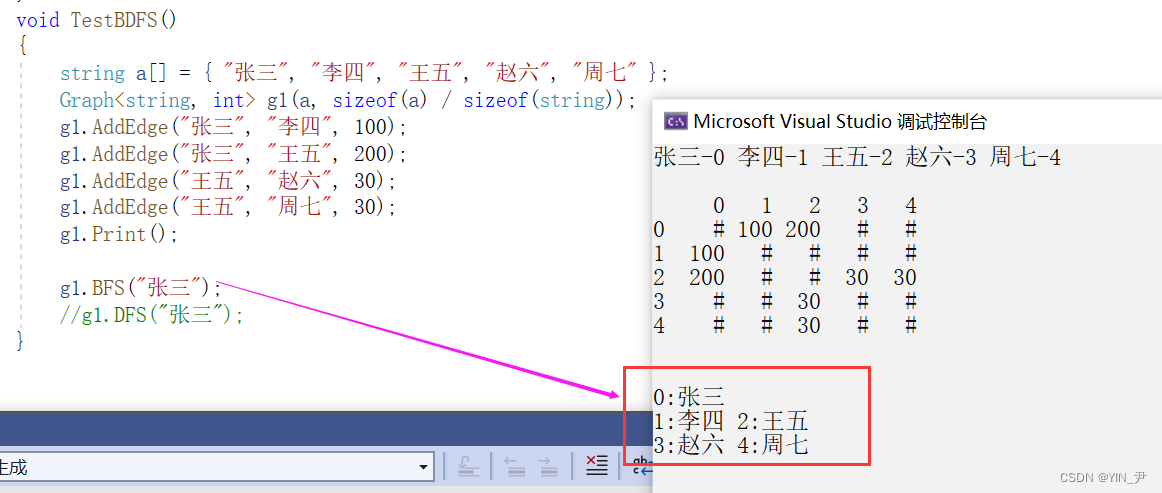
就实现分层了

2. 图的深度优先遍历（一条道走到黑）

那深度优先遍历又是什么呢？

其实我们之前学的二叉树的前序遍历就是一个深度优先遍历，就是先往深了去走，直到走不通了，再往回回溯。

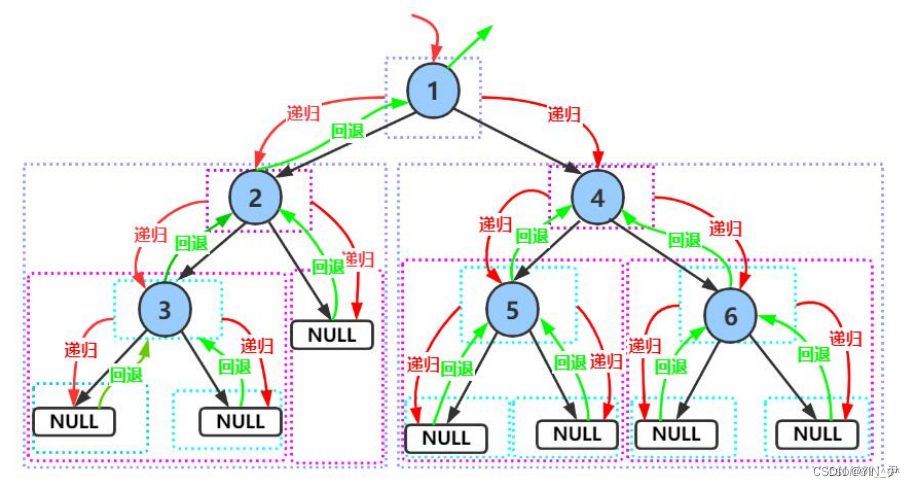
思路分析

那图的深度优先遍历我们来看一下：

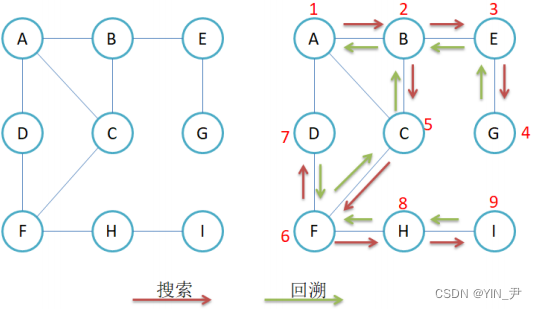
大家看这个图。
起点是A，那就从A开始，A遍历完，找一个与它直接相连的且没被遍历过的（所以我们这里还要标记遍历过的结点），那我们这里用的图结构是邻接矩阵的话，他找相连顶点的时候肯定就是按照那个结点对应的下标从小到大去找嘛。
那A找到的是B，然后B再去找一个与它邻接的顶点遍历（广度的话B遍历完就是继续找其它与A邻接的遍历），那B找到了C，那后面同样的，C再去找，接着…
一直走，一直走；
直到找到某一个顶点它的所有邻接顶点都被遍历过了，然后往回退，再去走其它没有走过的路径去遍历

所以我们还是用递归来搞就很简单嘛（先递推，再回归），DFS一般都是用递归来实现的。

代码实现

我们来写一下代码：

那这里递归的话我们可以在搞一个子函数，这基本上算固定套路了

那这里递归的时候我们传两个参数，首先是本次递归的起点下标（因为底层是邻接矩阵嘛），然后第二个是标记数组，这个要一直往下传，并且上一层递归的改变要延续到下一层，所以要传引用。不传这个的话你就搞一个全局的标记数组。
那递归里面的逻辑呢，很简单：
先访问当前顶点，然后找一个没访问过的邻接顶点，继续递归往深走，一直走到走不动了自动就向上返回了

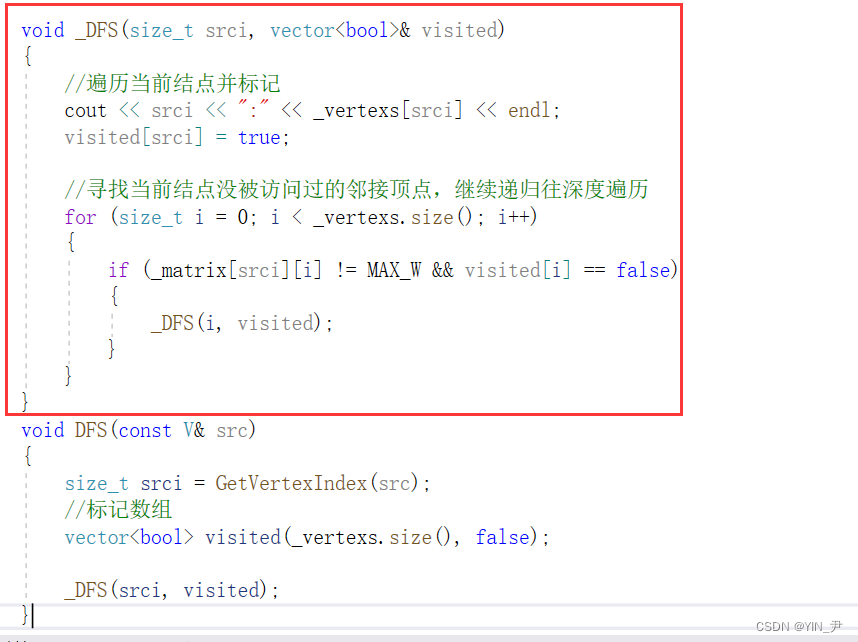
就写好了

测试

我们来测试一下：

就还用上面那个图吧

运行一下

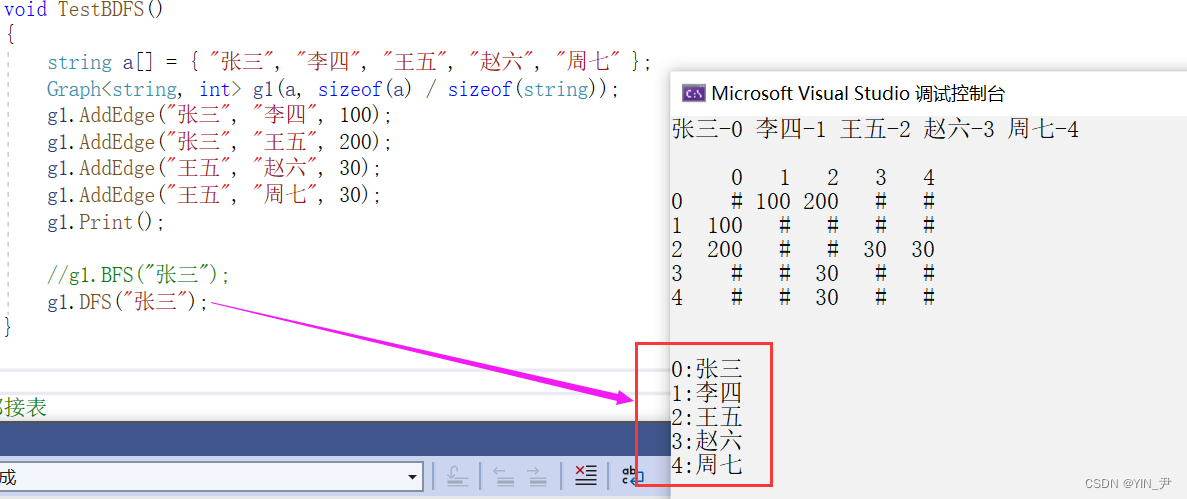
是没问题的，大家可以自己验证一下

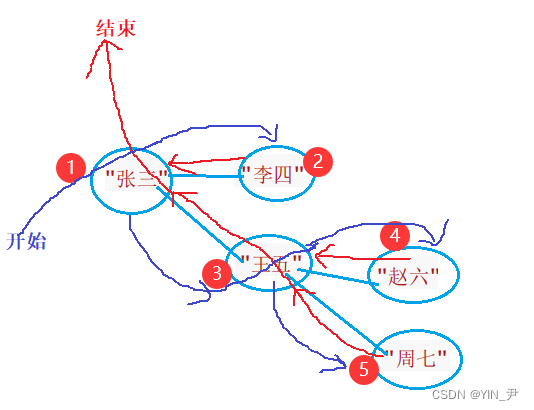
3. 对于非连通图情况的处理

上一篇文章我们有讲过连通图的概念：

那其实我们上面演示的例子，都是用的连通图。
对于连通图，不论是广度优先遍历还是深度优先遍历，我们上面的代码肯定都是没问题的，肯定能遍历完所有的顶点；

但是如果给我们的图是一个非连通的图呢？比如：

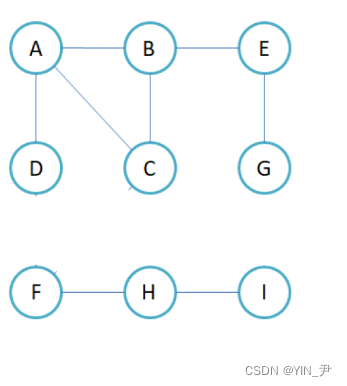
这样的。
那我们上面的代码针对这种情况会出现什么问题？
对于这种非连通图，如果我们再用上面的代码进行遍历的话，任取一个结点作为起点，比如还是A
那最终的结果就是我们只能遍历到上面的6个结点，最终遍历结束，还剩下面的3个结点我们是遍历不到的，因为它们跟上面的不连通，根本走不下来。

那我们如何解决这个问题呢？

其实也好办：
可再在搞一个循环，每遍历一次之后，我们就去那个标记数组里面看还有没有没被遍历到的顶点，如果有的话，就再取一个没被遍历到的点作为起点，再进行对应的DFS/BFS遍历。
直到标记数组里面所有的位置都变成true，那就证明所有的顶点都被遍历过了。
至此，图的遍历真正结束！

这样就可以解决非连通图的遍历问题！

4.源码

BFS

void BFS(const V& src)
{
	size_t srci = GetVertexIndex(src);
	//队列
	queue<int> q;
	//标记数组
	vector<bool> visited(_vertexs.size(), false);

	q.push(srci);
	visited[srci] = true;
	int levelSize = 1;

	while (!q.empty())
	{
		//每次循环打印一层
		while (levelSize--)
		{
			//取对头顶点front并打印
			int front = q.front();
			q.pop();
			cout << front << ":" << _vertexs[front] << " ";

			//把front顶点的邻接顶点入队列
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				//过滤掉已经入过队列的
				if (_matrix[front][i] != MAX_W && visited[i] == false)
				{
					q.push(i);
					visited[i] = true;
				}
			}
		}
		cout << endl;
		//更新levelSize为下一层的结点个数
		levelSize = q.size();
	}
	cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

DFS

void _DFS(size_t srci, vector<bool>& visited)
{
	//遍历当前结点并标记
	cout << srci << ":" << _vertexs[srci] << endl;
	visited[srci] = true;

	//寻找当前结点没被访问过的邻接顶点，继续递归往深度遍历
	for (size_t i = 0; i < _vertexs.size(); i++)
	{
		if (_matrix[srci][i] != MAX_W && visited[i] == false)
		{
			_DFS(i, visited);
		}
	}
}
void DFS(const V& src)
{
	size_t srci = GetVertexIndex(src);
	//标记数组
	vector<bool> visited(_vertexs.size(), false);

	_DFS(srci, visited);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

图结构我们用的是邻接矩阵，需要代码大家可以去上一篇文章获取…