顺序栈与链式栈

目录

栈的定义与结构

栈的实现

顺序栈的实现

 初始化空栈

 销毁栈

压栈

获取栈顶元素

出栈

判断栈是否为空

获取栈中有效数据的个数

链式栈的实现

初始化空栈

 销毁栈

压栈

获取栈顶元素

出栈

判断栈是否为空

获取栈中有效数据的个数

顺序栈与链栈的对比

---

栈的定义与结构

栈是只允许在固定的一端进行插入元素或删除元素的线性表；进行数据插入和删除操作的一端称为栈顶(top), 另一端称为栈底（bottom）；栈中的数据元素遵循后进先出（Last In First Out）的原则；

栈的基本操作：

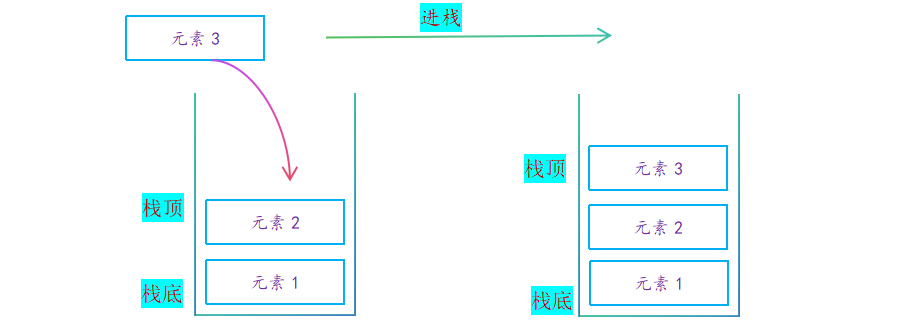
压栈：栈中插入元素的操作叫做压栈/入栈，插入数据在栈顶插入；

出栈：栈中删除元素的操作叫做出栈，删除数据也在栈顶；

栈的实现

栈可以由顺序表和链表实现,使用顺序存储结构实现栈存储结构称为顺序栈或数组栈，使用链式结构实现栈存储结构称为链式栈；

• 顺序栈的优点：

顺序栈的底层采用的是数组，当在栈顶插入或者删除元素时，可以通过下标进行插入或者删除，方便快捷，而且由于在内存中连续存储，缓存利用率高；

• 链式栈的缺点：

链式栈当插入数据（尾插）可以通过定义尾指针实现插入，但是当删除数据（尾删）时，需要找到 尾结点的前一个结点，而单向链表无法实现，只能采用双向链表，代价过大；

以单链表头结点作为栈顶，此时插入数据（头插），删除数据（头删），这样相比上述方案方便快捷，但是由于是链式存储，缓存利用率低；

顺序栈的实现

采用动态顺序表实现栈，当进行插入元素的操作时，若空间不够使用，可以通过动态内存函数realloc()函数扩容；

typedef int STDataType;
typedef struct Stack
{
	STDataType* nums;
	int top;//记录栈顶元素在顺序栈中的位置;
	int capacity;//记录栈的大小;
}Stack;

 初始化空栈

当栈顶元素的位置与栈底元素的位置相同，说明栈为空栈；空栈时，top的取值应该为多少？

若top=0表示空栈 ，当插入一个元素A0，则top=top+1即top=1；而top记录的是栈顶元素在顺序栈中的位置，此时top指向栈顶元素的下一个位置；若top不自增，top仍然为0，那么也将无法区分栈为空还是存在一个数据；

结论：top=0时，意味着top是栈顶元素的下一个位置；

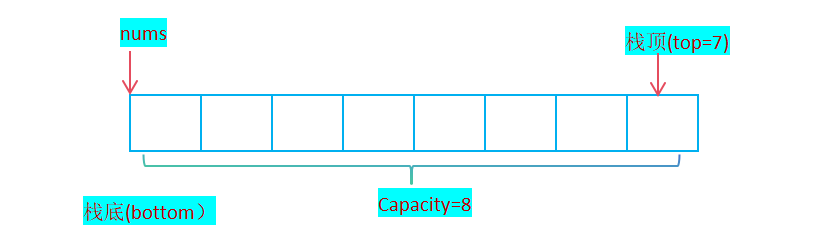
若top=-1表示空栈，当插入1个元素A0，则top=top+1即top=0;由于top记录的是栈顶元素在顺序栈中的位置，逻辑自洽；

结论：top=-1时，意味着top是栈顶元素位置；

void InitStack(Stack* ps)
{
	assert(ps != NULL);
	//开辟一定量的空间
	ps->nums = (STDataType*)malloc(4*sizeof(STDataType));
	//判断空间开辟是否成功
	if (ps->nums == NULL)
	{
		perror("malloc failed:");
		exit(-1);
	}
	ps->top = -1;
	ps->capacity = 4;
}

 销毁栈

//栈的销毁
void DestroyStack(Stack* ps)
{
	assert(ps != NULL);
 
	free(ps->nums);
	ps->nums = NULL;
 
	ps->top = 0;
	ps->capacity = 0;
}

压栈

压栈时需要先检查栈的容量，若容量已满，需要进行扩容；

• 栈满情况：（top=capacity-1）

//压栈
void StackPush(Stack* ps, STDataType x)
{
	assert(ps != NULL);
 
	//栈满扩容
	if (ps->top == ps->capacity - 1)
	{
		STDataType* tmp = (STDataType*)realloc(ps->nums, sizeof(STDataType)* 2 * (ps->capacity));
		if (tmp == NULL)
		{
			perror("realloc failed:");
			exit(-1);
		}
		ps->nums = tmp;
		ps->capacity = 2 * (ps->capacity);
	}
	//插入数据
	ps->nums[ps->top + 1]=x;
	ps->top++;
}

获取栈顶元素

//获取栈顶元素
STDataType StackTop(Stack* ps)
{
	assert(ps);
 
	//空栈
	assert(ps->top > (-1));
 
	return ps->nums[ps->top];
}

出栈

void StackPop(Stack* ps)
{
	assert(ps);
	//空栈时不可进行删除操作
	assert(ps->top > -1);
 
	ps->top = ps->top - 1;
}

判断栈是否为空

检测栈是否为空，栈为空返回true,否则返回false；

c语言默认没有布尔值(true/false)，使用时需包含头文件# include

bool StackEmpty(Stack* ps)
{
	assert(ps);
 
	return (ps->top == -1);
}

获取栈中有效数据的个数

int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top + 1;
}

• 测试如上接口函数：

//遍历栈中元素时，通过一边获取栈顶元素，一边删除的操作实现
int main()
{
	Stack st;
	InitStack(&st);
	StackPush(&st, 10);
	StackPush(&st, 20);
	StackPush(&st, 30);
	StackPush(&st, 40);
	StackPush(&st, 50);
	while (!StackEmpty(&st))
	{
		printf("%d->", StackTop(&st));
		StackPop(&st);
	}
	printf("\n");
	DestroyStack(&st);
	return 0;
}

运行结果：

链式栈的实现

采用带哨兵位的单链表实现，见下图存储结构

//链栈数据结点类型LinkStack声明
typedef int LSDataType;
typedef struct LinkStack
{
	LSDataType data;//数据域
	struct LinkStack* next;//指针域
}LinkStack;

链栈的4要素：

1.栈空条件：phead->next=NULL

2.栈满条件：对于链栈而言，基本不存在栈满的情况，除非内存已经没有可以使用的空间，不需要考虑；

3.进栈操作：头插

4.出栈操作：头删

初始化空栈

建立一个空栈实际上是创建哨兵位的结点，并将其的next置为空指针；

//为将哨兵位结点带出，采用返回值的方案
LinkStack* InitStack(LinkStack* phead)
{
	LinkStack* phead = (LinkStack*)malloc(sizeof(LinkStack));
	if (phead == NULL)
	{
		perror("malloc fail:");
		exit(-1);
	}
	phead->next = NULL;
	return phead;
}

 销毁栈

释放所有动态开辟的结点空间；

//销毁栈
//先保存当前结点的下一个结点，然后释放当前结点;
void DestroyStack(LinkStack* phead)
{
	assert(phead);
	LinkStack* cur = phead;
	LinkStack* curnext = cur->next;
	while (curnext != NULL)
	{
		free(cur);
		cur = curnext;
		curnext = cur->next;
	}
	//此时cur指向尾结点
	free(cur);
	cur = NULL;
}

压栈

void StackPush(LinkStack* phead, LSDataType x)
{
	assert(phead);
	//开辟新结点
	LinkStack* newnode = malloc(sizeof(LinkStack));
	if (newnode==NULL)
	{
		perror("malloc failed:");
		exit(-1);
	}
	newnode->data = x;
	//头插=压栈
	newnode->next = phead->next;
	phead->next = newnode;
}

获取栈顶元素

在栈不为空的条件下，将哨兵位结点后的头结点的数据返回；

//获取栈顶元素
LSDataType LinkStTop(LinkStack* phead)
{
	assert(phead);
	//空栈
	assert(phead->next != NULL);
 
	return phead->next->data;
}

出栈

//出栈
void StackPop(LinkStack* phead)
{
	assert(phead);
    //空栈不可删除
	assert(phead->next != NULL);
 
	LinkStack* Second = phead->next->next;
	free(phead->next);//释放首结点
	phead->next = Second;
}

判断栈是否为空

检测栈是否为空，栈为空返回true,否则返回false；

//判断栈是否为空
bool StackEmpty(LinkStack* phead)
{
	assert(phead);
 
	return (phead->next == NULL);
}

获取栈中有效数据的个数

//获取栈中有效数据的个数
int StackSize(LinkStack* phead)
{
	assert(phead);
	int count = 0;//计数
	LinkStack* cur = phead->next;
	while (cur != NULL)
	{
		count++;
		cur = cur->next;
	}
	return count;
}

顺序栈与链栈的对比

顺序栈与链栈的时间复杂度均为O(1);

空间性能由于顺序栈是动态内存函数开辟的，势必会有一定空间的浪费，但是存取定位方便；链栈恰好弥补了上述缺点，但是链栈缓存利用率不高；

当线性表中元素个数变化大或者不知道元素个数有多少，采用链式栈；

当事先知道线性表的大致长度，采用顺序栈存储结构效率高；