【算法练习Day15】平衡二叉树&&二叉树的所有路径&&左叶子之和

​📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：练题
🎯长路漫漫浩浩，万事皆有期待

平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode）

什么是平衡二叉树呢？
该树的每一个节点的两棵子树高度差的绝对值不高于1，则说明该二叉树是平衡二叉树。

思路是这样的：我们可以写一个函数，它的作用是帮我们算出两子树最高的那一个是多高，直到返回到根节点，在比较各个子树的高矮时，如果碰到两子树相差过高，则直接返回-1，在下面比较时我们直接能判断出来。函数的书写我们使用后序遍历的思路，因为我们要判断一个节点的子树，相差是否大于1，然后向上返回，只有后序遍历才能先遍历到两子树。

class Solution {
public:
    int getHeight(TreeNode* node)
    {
        if(node==nullptr)
        {
            return 0;
        }
        int leftHeight=getHeight(node->left);
        if(leftHeight==-1)
        {
            return -1;
        }
        int rightHeight=getHeight(node->right);
        if(rightHeight==-1)
        {
            return -1;
        }
        return abs(leftHeight-rightHeight)>1?-1:1+max(leftHeight,rightHeight);
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root)==-1?false:true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

递归的思路就是遍历到空节点就是左右子树为0，所以返回0，然后创建两个整形来保存数据，进入递归分别保存左右子树的高度，然后在最后处理中间节点时作比较，如果高度大于1返回-1，到上一层if判断如果为-1，直接返回-1跳出，如果不是继续遍历，接着将结果赋给整型变量存储。我们是使用判断子树高度的思想来间接判断各子树是否能够平衡。

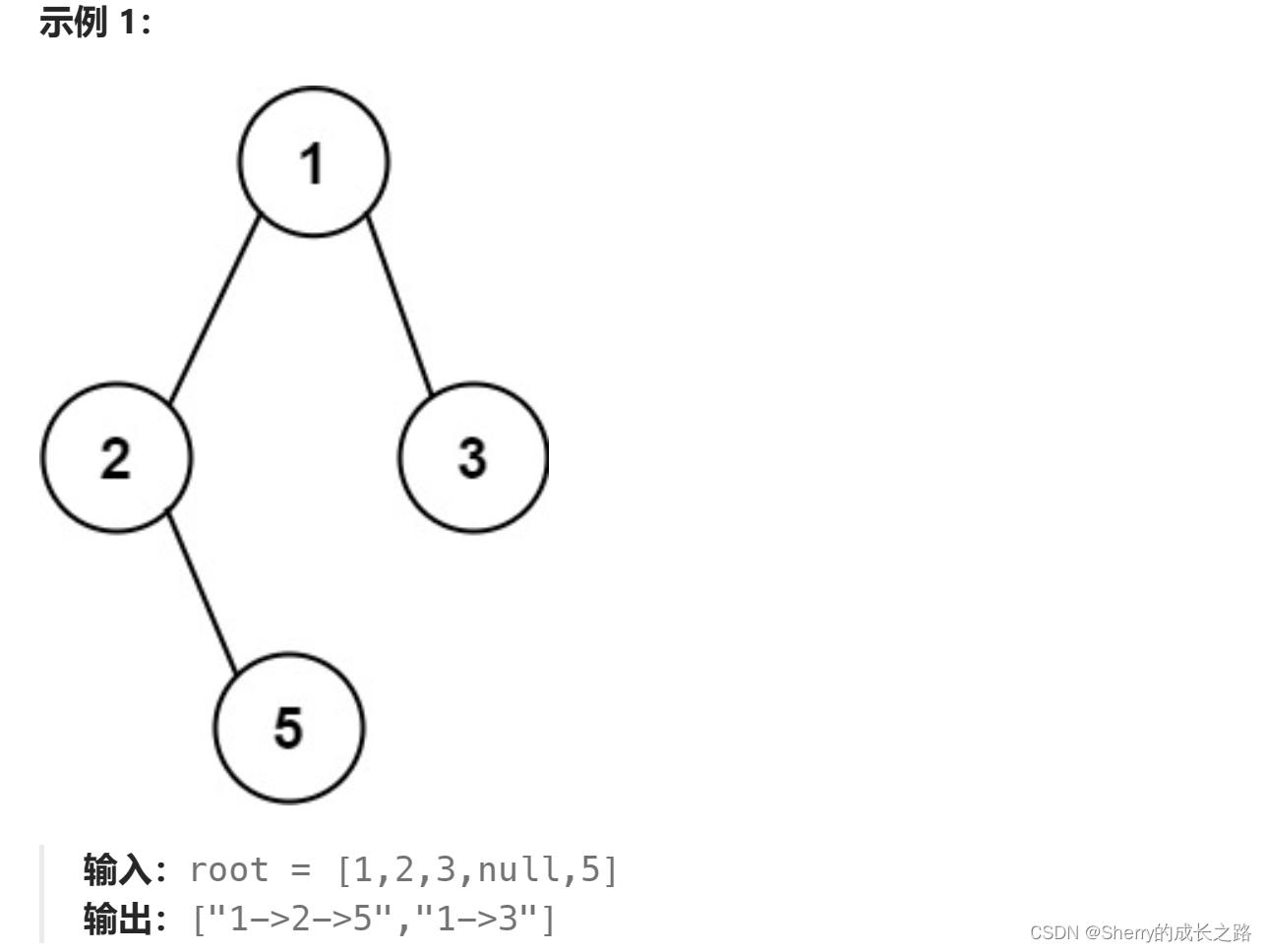
二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）

这道题就是遍历二叉树的所有节点然后将他们用->连接起来，每一条不同的路径使用不同的字符串，而不是所有路径都是一个字符串。

class Solution {
public:
void get(TreeNode*root,vector<int>& path,vector<string>&result){
    path.push_back(root->val);
    if(root->left==NULL&&root->right==NULL){
        string path2;
      for(int i=0;i<path.size()-1;i++){
          path2+=to_string(path[i]);
          path2+="->";
      }
      path2+=to_string(path[path.size()-1]);
      result.push_back(path2);
    }
    if(root->left){
        get(root->left,path,result);
        path.pop_back();
    }
    if(root->right){
        get(root->right,path,result);
        path.pop_back();
    }
}
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string>result;
        vector<int>path;
        get(root,path,result);
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

这里我们采用前序遍历来写函数的具体实现，要将加入节点写到最前面，因为我们的递归终止条件是遇到叶子节点时，跳出递归返回。需要注意的是每次写完递归之后，还要再下面写下pop，原因是在进入下一个不同路径之前，我们需要pop函数帮助我们弹出这条路径的节点，才能让数组加入下一条路径的数据，而将该数组转化为字符串形式和添加->等这些操作都在，递归的终止条件下进行。

代码精简后：

class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
    	vector<string> ret;
        string path;
        if(root==nullptr)
        {
            return ret;
        }
        dfs(root,path);
        return ret;
    }
    void dfs(TreeNode* root,string path)
    {
        path+=to_string(root->val);// 中
        if(root->left==nullptr&&root->right==nullptr)
        {
            ret.push_back(path);
            return;
        }
        path+="->";//回溯
        if(root->left)dfs(root->left,path);// 左
        if(root->right)dfs(root->right,path); // 右
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

左叶子之和

404. 左叶子之和 - 力扣（LeetCode）

这道题是求出该树中左叶子的节点值和，左叶子是左子树和右子树的全部左子叶。解题思路是：写一个函数，分别遍历各节点的左子叶是不是叶子节点，如果是则加入进总数中，最后返回总数。这里我们判断的是左子叶的上一个节点，而不是等到判断到左子叶节点在做处理，这里我们仍然使用后序遍历的方法，将各节点左子叶的总数依次返回直到根节点为止。

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right== NULL) return 0;

        int leftValue = sumOfLeftLeaves(root->left);    // 左
        if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况
            leftValue = root->left->val;
        }
        int rightValue = sumOfLeftLeaves(root->right);  // 右

        int sum = leftValue + rightValue;               // 中
        return sum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

我们在遍历右侧子树时，也就是后序遍历中的右半部分，只管递归而不做判断的处理，因为要算得是左叶子节点的值，当它一直递归下去往上返回后还是交给左边递归来进行节点的判断。

总结：

今天我们完成了平衡二叉树、二叉树的所有路径、左叶子之和三道题，相关的思想需要多复习回顾。接下来，我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。

当然，本文仍有许多不足之处，欢迎各位小伙伴们随时私信交流、批评指正！我们下期见~