激活函数与loss的梯度

激活函数：
最开始由生物学家对青蛙的神经元机制进行研究发现，青蛙的神经元有多个输入x0、x1、x2，响应值是他们加权后的结果，但响应值如果小于阈值，则不会响应，而只有大于阈值时，才会有固定的响应。

这就类似于阶梯函数

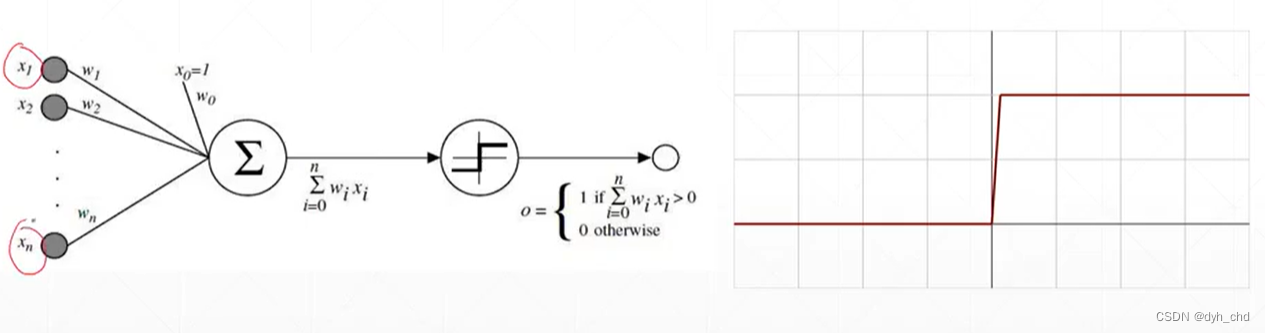
但阶梯函数由于不连续，故不可导。科学家提出了连续光滑的激活函数：sigmoid / logistic

sigmoid

使用的范围比较广，因为它能把输出值的范围压缩在0-1之间，如概率，还有像素值RGB都是0-1的大小。

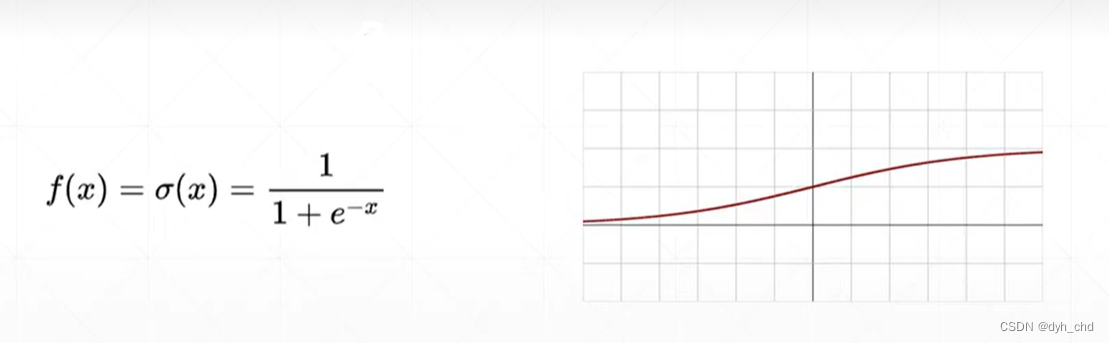
当输入很小的时候，响应接近于0，当输入很大的时候，响应接近于1。

对sigmoid函数进行求导

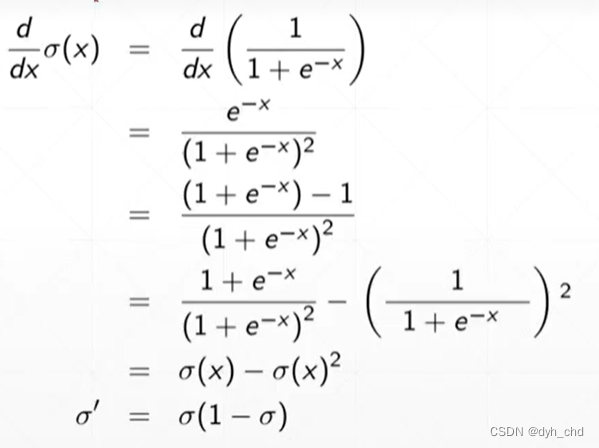
但sigmoid函数有缺陷：
在趋近于正无穷的地方，σ的导数接近于0，则参数θ更新后仍为θ，长时间参数得不到更新这个情况也叫做梯度离散。

sigmoid在pytorch上的实现

import torch
a = torch.linspace(-100, 100, 10)
a

torch.sigmoid(a)
# 也可以用F.sigmoid(a)
# from torch.nn import function as F
1
2
3
4
5
6
7

tanh

该激活函数在RNN中用的较多

由sigmoid变换得到，值的区间为 -1~1

将tanh进行求导：

与sigmoid相似之处是，只要有激活函数的值，导数的值也可直接得到。

a = torch.linspace(-1, 1, 10)

torch.tanh(a)
1
2
3

ReLU

深度学习的经典激活函数，比较简单基础

在x<0时，梯度为0，在x>=0时，梯度为1，在向后传播时梯度计算非常方便，且不会放大和缩小梯度，避免梯度离散和梯度爆炸。

a = torch.linspace(-1, 1, 10)

torch.relu(a)

F.relu(a)
1
2
3
4
5

MSE_LOSS

一般用的是均方误差MSE，还有一种用于分类问题的误差留到之后学习。

MSE的基本形式，以线性感知机xw+b为例：

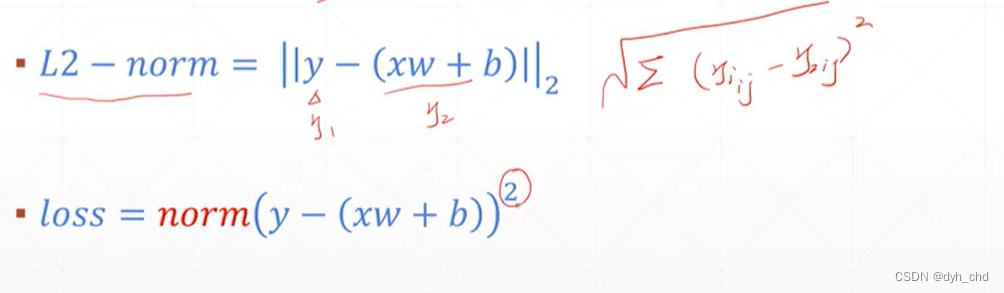在torch用L2-norm实现再加平方即为loss

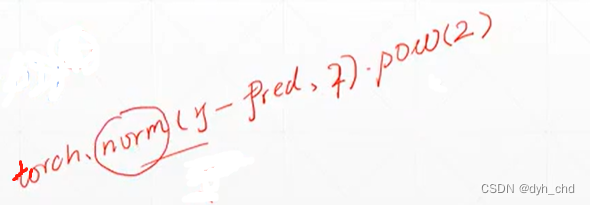
loss求导：

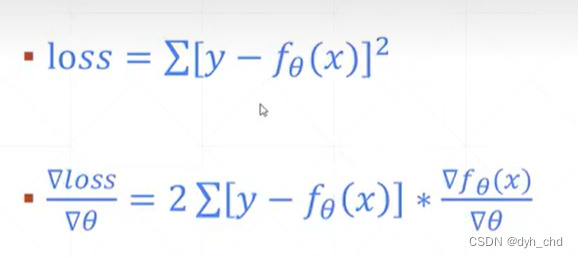
使用pytorch自动求导
先计算mse
使用的是最简单的线性感知机，且此时b=0，x初始化为1，w的dim=1，初始化为2


自动求导

直接求导会报错

w初始化没有设置为需要导数信息，直接求导会报错，故要对w信息进行更新。

w更新后图也要进行更新，故mse也要进行更新，否则还是报错

w.requires_grad_()

mse = F.mse_loss(torch.ones(1), x*w)

torch.autograd.grad(mse, [w])
1
2
3
4
5

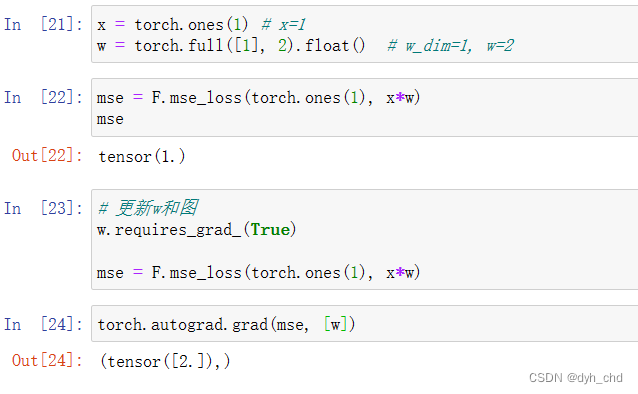
loss = (1-2)**2 = 1
grad 是 loss对w的求导：
2（1 - x*w) * (-x) = 2 (1-2) (-1) = 2

补充：
在loss上调用backward()，会从后往前完成这条路径上的梯度计算，然后再手动查看如：w.grad

#同样需要更新w和图
w.requires_grad_()

mse = F.mse_loss(torch.ones(1), x*w)

mse.backward()

w.grad
1
2
3
4
5
6
7
8

autograd方法与backward方法对比：

Cross Entropy Loss

是用于分类中的误差，之后再深入了解。这次主要了解与它紧密结合使用的激活函数–softmax。

作用：以模型最终输出三个结果值为例，将他们转化为概率值，且和为1，可以发现，转化后的结果相较于转化前，较大值与较小值相差倍数更大，金字塔效应。

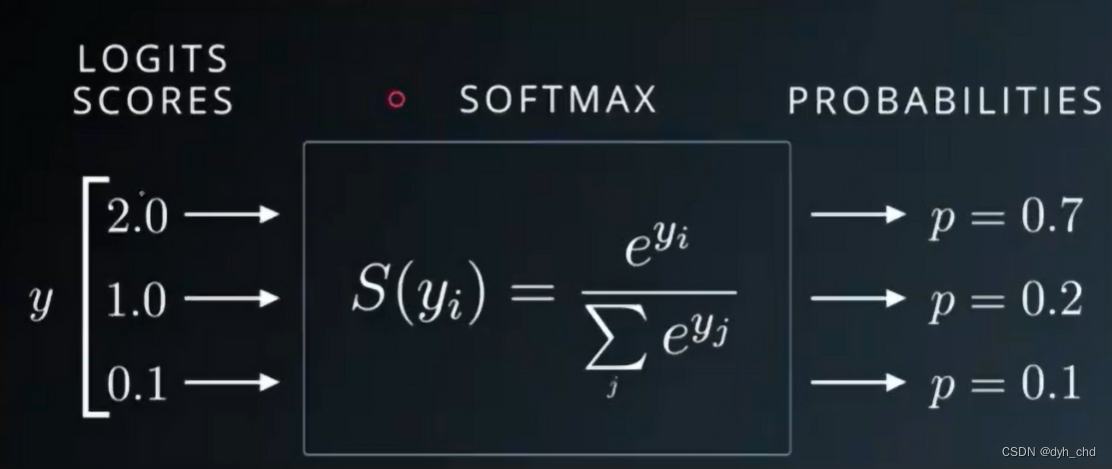
softmax函数求导：

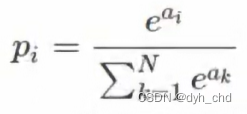
其中i和j取值范围一样，分别表示第几个概率值和第几个输入

两种情况
1、 i = j时
导数结果为正数 Pi（1-Pj）

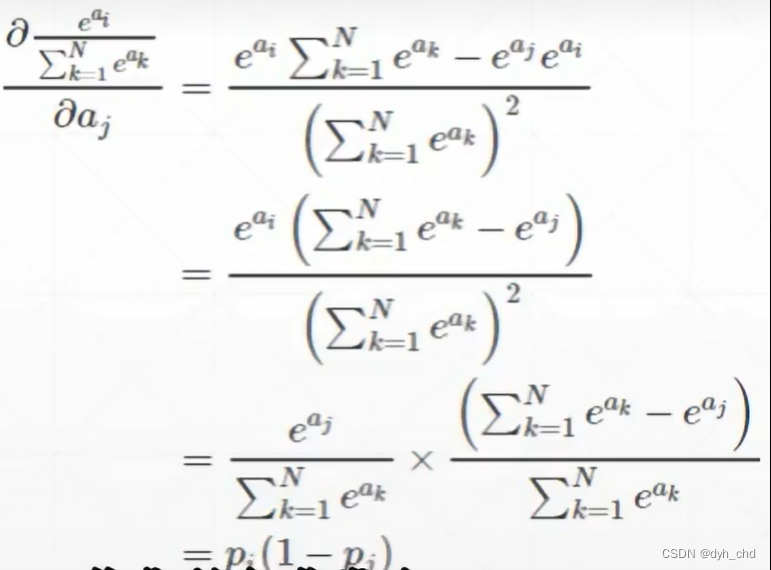
2、i ≠ j时
导数结果为负数 -PiPj

总结：

pytorch实现

a = torch.rand(3)
a.requires_grad_()

p = F.softmax(a, dim=0)

torch.autograd.grad(p[0], [a], retain_graph=True)
							#保留图，若没有保留，下次还有重新更新求导信息
torch.autograd.grad(p[1], [a])							
1
2
3
4
5
6
7
8