数据结构--》数组和广义表：从基础到应用的全面剖析

        数据结构为我们提供了组织和处理数据的基本工具。而在这个广袤的数据结构领域中，数组和广义表是两个不可或缺的重要概念。它们作为线性结构的代表，在算法与应用中扮演着重要的角色。

        无论你是初学者还是进阶者，本文将为你提供简单易懂、实用可行的知识点，帮助你更好地掌握数组和广义表在数据结构和算法中的重要性，进而提升算法解题的能力。接下来让我们开启数据结构与算法的奇妙之旅吧。

目录

数组的定义

数组的顺序表示和实现

矩阵的压缩存储

广义表的定义

广义表的存储结构

---

数组的定义

数组是一组偶对(下标值，数据元素值)的集合。在数组中对于一组有意义的下标，都存在一个与其对应的值。一维数组对应着一个下标值，二维数组对应着两个下标值，如此类推。

数组是由n(n>1)个具有相同数据类型的数据元素 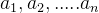组成的有序序列，且该序列必须存储在一块地址连续的存储单元中。数组具有以下特点：

1）数组中的数据元素具有相同数据类型

2）数组是一种随机存取结构，给定一组下标，就可以访问与其对应的数据元素。

3）数组中的数据元素个数是固定的。

数组的抽象数据类型定义：

由上述定义知，n维数组中有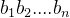个数据元素，每个数据元素都受到n维关系的约束。

数组的顺序表示和实现

数组一般不做插入和删除操作，也就是说数组一旦建立，结构中的元素的个数和元素间的关系就不再发生变化。因此一般都是采用顺序存储的方法来表示数组。

计算机的内存结构是一堆(线性)地址结构，对于多维数组，将其存放(映射)到内存一维结构时，有个次序约定问题。即必须按某种次序将数组元素排成一列序列，然后将这个线性序列存放到内存中。

二维数组是最简单的多维数组，以此为例说明多维数组存放(映射)到内存一维结构时的次序约定问题。

二维数组的两种存储方式（以行序为主、以列序为主）：

举个例子：

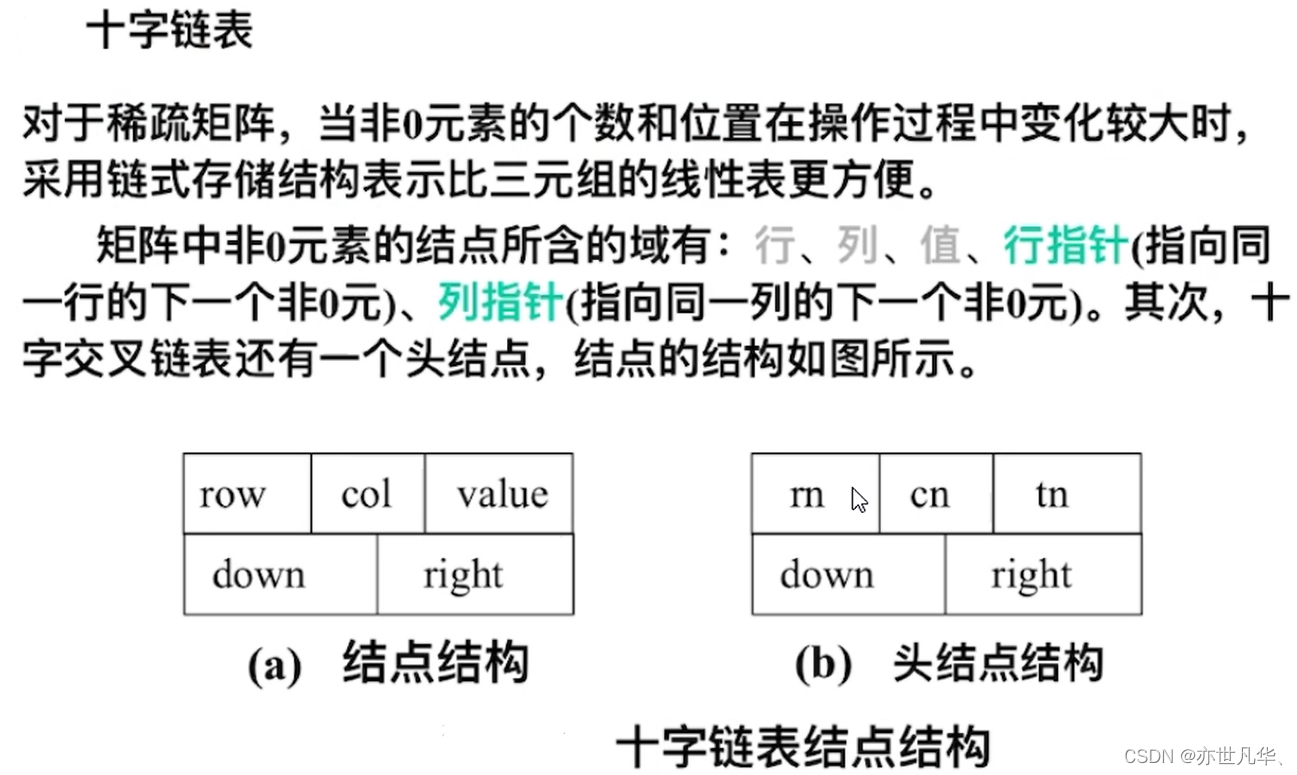
矩阵的压缩存储

        在科学与工程计算问题中，矩阵是一种常用的数学对象，在高级语言编程时，通常将一个矩阵描述为一个二维矩阵。这样可以对其元素进行随机存取，各种矩阵运算也非常简单。

        对于高阶矩阵，若其中非零元素呈某种规律分布或者矩阵中有大量的零元素，若仍然用常规方法存储，可能存储重复的非零元素或零元素，将造成存储空间的大量浪费。所以要对这类矩阵进行压缩存储。

注意：多个相同的非零元素只分配一个存储空间；零元素不分配空间。

接下来我们要掌握 特殊矩阵 与 稀疏矩阵 的压缩存储方式。

广义表的定义

        广义表是线性表的推广和扩充，在人工智能领域中应用十分广泛。我们把线性表定义为n(n⩾0)个元素a1,a2,...an的有穷序列，该序列中的所有元素具有相同的数据类型且只能是原子项(所谓原子项可以是一个数或一个结构，是指结构上不可再分的。)若放松对元素的这种限制，容许它们具有其自身结构，就产生了广义表的概念。

广义表(Lists，又称为列表)：是由n(n⩾0)个元素组成的有穷序列：LS=(a1,a2,...an)

广义表的存储结构

由于广义表中的数据元素具有不同的结构，通常用链式存储结构表示，每个数据元素用一个结点表示。因此，广义表中就有两类结点：

一类是表结点：用来表示广义表项，由标志域，表头指针域，表尾指针域组成

一类是原子结点：用来表示原子项，由标志域，原子的值域组成。

只要广义表非空，都是由表头和表尾组成。即一个确定的表头和表尾就唯一确定一个广义表。

什么是广义表？请简述广义表与线性表的区别？

        广义表（Generalized List）是一种扩展了线性表的数据结构，它允许元素既可以是单值，也可以是子表。广义表通过递归方式定义，可以包含任意嵌套层级的子表，从而形成一个更加复杂和有层次结构的数据集合。

        与广义表相对应的是线性表（Linear List），线性表仅包含单值元素，每个元素都有一个后继元素，形成一个线性结构。线性表是最简单和最常见的数据结构之一，例如数组就是线性表的一种实现。

广义表与线性表的区别主要有以下几点：

1. 元素类型：线性表的元素只能是单值，而广义表的元素可以既是单值，也可以是子表。这使得广义表能够表示更加复杂和有层次结构的数据关系。

2. 结构特点：线性表是一种线性结构，每个元素都有唯一的后继元素，形成了一个简单的序列。而广义表则具有更加复杂的层次结构，可以包含任意嵌套层级的子表，形成了一个树状结构。

3. 操作灵活性：由于广义表具有更复杂的结构，因此在操作和处理数据时，广义表比线性表更加灵活。广义表可以使用递归的方式进行遍历和操作，可以处理各种复杂的数据关系，而线性表则相对简单。

综上所述，广义表是一种扩展了线性表的数据结构，允许元素既可以是单值，也可以是子表。广义表具有更加复杂的层次结构和操作灵活性，可以更好地表示和处理各种复杂的数据关系。

一个广义表是(a,(a,b),d,e,(a,(i,j),k))，请画出该广义表的链式存储结构：

                +---+         +---+         +---+         +---+
                | a |---+     |   |---+     | d |---+     | e |
                +---+   |     +---+   |     +---+   |     +---+
                        |             |             |
                        |     +---+   |     +---+   |
                        +---->| a |   +---->| b |   |
                        |     +---+   |     +---+   |
                        |             |             |
                        |     +---+   |             |
                        +---->| i |   +-------------+
                              +---+
                              |
                              |
                              |
                              |     +---+
                              +---->| j |
                                    +---+
                                    |
                                    |
                                    |
                                    |
                                    |     +---+
                                    +---->| k |
                                          +---+