-
【状态估计】将变压器和LSTM与卡尔曼滤波器结合到EM算法中进行状态估计(Python代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录

💥1 概述
文章来源:

卡尔曼滤波器需要模型的真实参数,并递归地求解最优状态估计期望最大化(EM)算法适用于估计卡尔曼滤波之前不可用的模型参数,即EM-KF算法。为了提高EM-KF算法的准确性,作者提出了一种状态估计方法,该方法在序列到序列的编码器-解码器(seq2seq)框架下,将长-短期存储器网络(LSTM)、变压器和EM-KF方法相结合。对线性移动机器人模型的仿真表明,新方法更准确。
- 卡尔曼滤波需要模型的真实参数,并递归求解最优状态估计。期望最大化(EM)算法适用于估计卡尔曼滤波前不可用的模型参数,即EM-KF算法。
- 为了提高EM-KF算法的精度,该文在序列编码器-解码器(seq2seq)的框架中,结合长短期记忆网络(LSTM)、变压器和EM-KF算法,提出了一种状态估计方法。
我们在seq2seq中提出了用于状态估计的编码器-解码器框架,该状态估计等效于编码和解码观察。
- 之前将LSTM整合到KF的工作是采用LSTM编码器和KF 译码器。我们建议LSTM-KF采用LSTM编码器和EM-KF解码器。
- 在EM-KF解码器之前,用变压器编码器代替LSTM编码器,我们称之为 变压器-KF.
- 集成变压器和LSTM,我们称之为TL-KF。
集成变压器和LSTM在滤波前对观察进行编码,使EM算法更容易估计参数。
- 将Transformer和LSTM作为观测的编码器-解码器框架相结合,可以更有效地描述状态,衰减噪声干扰,削弱状态马尔可夫性质的假设和观测的条件独立性。这可以增强状态估计的精度和鲁棒性。
- 基于多头自注意和残余连接的变压器可以捕获长期依赖性,而LSTM编码器可以对时间序列进行建模。TL-KF是变压器、LSTM和EM-KF的组合,可用于参数未知的系统的状态估计。
- 卡尔曼平滑可以改善卡尔曼滤波,但在TL-KF中,滤波足够精确。因此,经过离线训练进行参数估计后,可以采用KF进行在线估计。


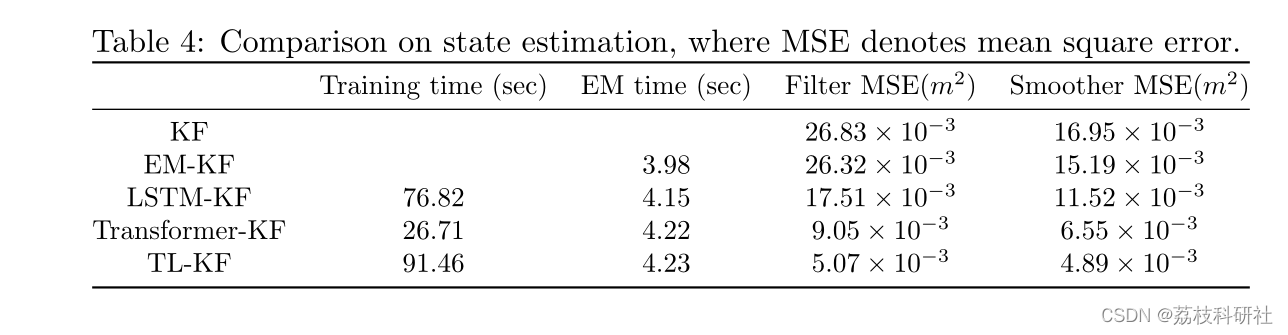
📚2 运行结果


部分代码:
kft = KalmanFilter( A,C,Q,R,B,D,m0,P0, random_state=random_state )# model should be state, observation = kft.sample( n_timesteps=step, initial_state=m0 )# provide data #filtered_state_estimatet, f_covt = kft.filter(observation) #smoothed_state_estimatet, s_covt = kft.smooth(observation) ''' Step 2: Initialize our model ''' # specify parameters transition_matrix = A transition_offset = B observation_matrix = C observation_offset = D transition_covariance = 0.02*np.eye(3) observation_covariance = np.eye(1) initial_state_mean =[0,0,1] initial_state_covariance = 5*np.eye(3) # sample from model kf = KalmanFilter( transition_matrix, observation_matrix, transition_covariance, observation_covariance, transition_offset, observation_offset,initial_state_mean,initial_state_covariance, random_state=random_state, em_vars=[ #'transition_matrices', 'observation_matrices', 'transition_covariance','observation_covariance', #'transition_offsets', 'observation_offsets', 'initial_state_mean', 'initial_state_covariance' ]class TransformerBlock(nn.Module): """ Bidirectional Encoder = Transformer (self-attention) Transformer = MultiHead_Attention + Feed_Forward with sublayer connection """ def __init__(self, hidden, attn_heads, feed_forward_hidden, dropout): """ :param hidden: hidden size of transformer :param attn_heads: head sizes of multi-head attention :param feed_forward_hidden: feed_forward_hidden, usually 4*hidden_size :param dropout: dropout rate """ super().__init__() self.attention = MultiHeadedAttention(h=attn_heads, d_model=hidden) self.feed_forward = PositionwiseFeedForward(d_model=hidden, d_ff=feed_forward_hidden, dropout=dropout) self.input_sublayer = SublayerConnection(size=hidden, dropout=dropout) self.output_sublayer = SublayerConnection(size=hidden, dropout=dropout) self.dropout = nn.Dropout(p=dropout) self.hidden = hidden🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
- @article{shi2021kalman,
- author={Zhuangwei Shi},
- title={Incorporating Transformer and LSTM to Kalman Filter with EM algorithm for state estimation},
- journal={arXiv preprint arXiv:2105.00250},
- year={2021},
- }
🌈4 Matlab代码及文章讲解
-
相关阅读:
【Lua基础 第6章】 Lua 数组、Lua的错误处理、Lua 模块与包、元表(Metatable)和元方法
基于SSM+Vue的线上学习网站
零基础学python之集合
CLUE模型如何实现对未来土地利用/土地覆盖的时空预测
简单Spring源码解析(一) 容器启动
lua调用C/C++的函数,十分钟快速掌握
河北吉力宝打造步力宝智能康养鞋,助力健康中国行
java spring MVC环境中实现WebSocket
C++基础——基础语法
CSS的初步学习
- 原文地址:https://blog.csdn.net/m0_64583023/article/details/133615649