-
机器学习基础之《回归与聚类算法(1)—线性回归》
一、线性回归的原理
1、线性回归应用场景
如何判定一个问题是回归问题的,目标值是连续型的数据的时候房价预测
销售额度预测
贷款额度预测、利用线性回归以及系数分析因子2、线性回归定义
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式找到一种函数关系,来表示特征值和目标值之间的关系
3、函数关系

(1)首先假定特征值x1、x2、x3
(2)目标值是h(w)
(3)每个特征前还有个系数,w1、w2、w3,叫做权重值,也叫回归系数
(4)右边+b,叫做偏置系数
(5)只有一个自变量的情况称为单变量回归,大于一个自变量情况的叫做多元回归用习惯的写法:
y = w1x1 + w2x2 + w3x3 + ... + wnxn + b
= wTx + bPS:wT叫做w的转置
例子:
期末成绩:0.7×考试成绩 + 0.3×平时成绩
预测房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率4、广义线性模型
线性回归当中的关系有两种,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征举例子(1)线性关系

特征只有一个房屋面积,预测房屋价格,在一个平面当中,可以找到一条直线去拟合他们之间的关系,y = kx + b
如果有两个特征:

要拟合x1、x2和y之间的关系,y = w1x1 + w2x2 + b
如果在单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想,记住这种关系即可(2)非线性关系

为什么非线性关系,也叫线性模型
线性模型
自变量一次
y = w1x1 + w2x2 + w3x3 + ... + wnxn + b
参数一次
y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + ... + b
就是w和x有一个是一次的,不是多次的,都可以叫线性模型
(3)线性关系&线性模型
线性关系一定是线性模型,线性模型不一定是线性关系二、线性回归的损失和优化原理
1、目标:求模型参数
模型参数能够使得预测准确2、预测房屋价格
真实关系:真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率随意假定关系:预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
当我们把特征值代入到假定的关系当中,预测价格和真实价格肯定有一个误差,如果我们有一种方法,将这个误差不断的减少,让它最终接近于0的话,是不是就意味着模型参数比较准确了
3、真实值和预测值之间的差距如何去衡量
衡量的关系,叫做损失函数/cost/成本函数/目标函数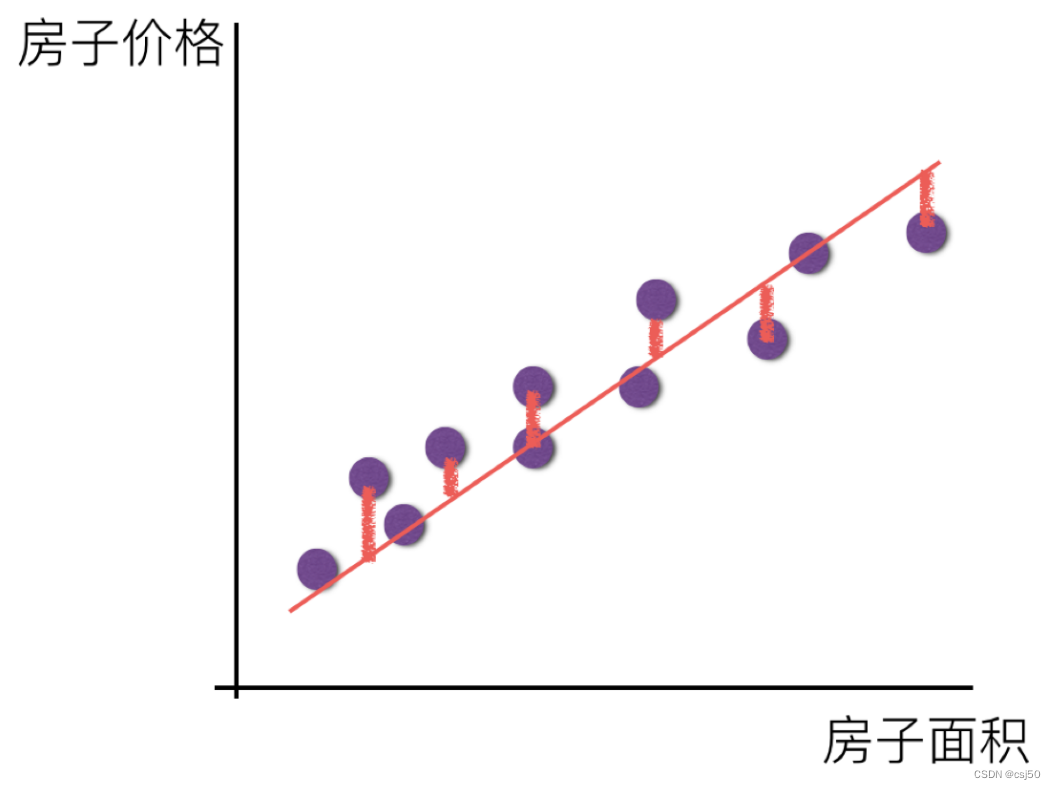
目标:希望找到所有真实的样本,到预测的距离之和比较小,可以求出比较合适的权重和偏置
4、损失函数

y1:真实值
hw(x1):预测值
预测值-真实值,再求个平方,因为预测值有可能小于真实值
这个公式又叫最小二乘法,有计算平方,又希望这个损失越小越好为什么不用绝对值:
(1)如果不加绝对值或者平方,距离是会相互抵消的,这是不正确的
(2)加绝对值也就是平方再开根号,而且绝对值求导麻烦,所以直接用了平方如何去减少这个损失,使我们预测的更加准确些?既然存在了这个损失,我们一直说机器学习有自动学习的功能,在线性回归这里更是能够体现。这里可以通过一些优化方法去优化(其实是数学当中的求导功能)回归的总损失!
5、优化算法
正规方程和梯度下降,正规方程相当于一个天才,梯度下降相当于一个勤奋努力的普通人6、正规方程(用的少)

通过一个矩阵运算,先求特征值转置,然后乘以它本身,再求一个逆,再乘以它的转置,再乘以y,直接求出w权重理解:X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果
7、梯度下降(常用)
一开始随便给一组权重和偏置,不断的改进、试错
第二组的w1、w0等于上一组的w1、w0减去一个数
我们通过两个图更好理解梯度下降的过程:


理解:α为学习速率(步长),需要手动指定(超参数),α旁边的整体表示方向(坡度最陡的)
沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新w值
使用:面对训练数据规模十分庞大的任务,能够找到较好的结果8、动态图演示

三、线性回归API
1、sklearn.linear_model.LinearRegression(fit_intercept=True)
通过正规方程优化
fit_intercept:是否计算偏置(截距)
查看参数
LinearRegression.coef_:回归系数
LinearRegression.intercept_:偏置2、sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
通过梯度下降优化,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型
loss:损失函数
loss="squared_loss",普通最小二乘法
fit_intercept:是否计算偏置
learning_rate:学习率(步长),指定学习率算法
'constant':eta = eta0
'optimal':eta = 1.0 / (alpha * (t + t0)) [default]
'invscaling':eta = eta0 / pow(t, power_t),看动态图演示,步长一开始很长,越接近最低点,越小
power_t=0.25:存在父类当中
对于一个常数值的学习率来说,可以使用learning_rate=’constant’ ,并使用eta0来指定学习率
查看参数
SGDRegressor.coef_:回归系数
SGDRegressor.intercept_:偏置四、波士顿房价预测
1、数据集地址
下载数据集:https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data该数据集统计了13种可能影响房价的因素和该类型房屋的均价,期望构建一个基于13个因素进行房价预测的模型

2、分析流程
流程:
1)获取数据集
2)划分数据集
3)特征工程
无量纲化 - 标准化
4)预估器流程
fit() --> 模型
coef_ intercept_
5)模型评估3、代码 day03_machine_learning.py
- from sklearn.datasets import load_boston
- from sklearn.model_selection import train_test_split
- from sklearn.preprocessing import StandardScaler
- from sklearn.linear_model import LinearRegression, SGDRegressor
- def linear1():
- """
- 正规方程的优化方法对波士顿房价进行预测
- """
- # 1、获取数据
- boston = load_boston()
- # 2、划分数据集
- x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)
- # 3、标准化
- transfer = StandardScaler()
- x_train = transfer.fit_transform(x_train)
- x_test = transfer.transform(x_test)
- # 4、预估器
- estimator = LinearRegression()
- estimator.fit(x_train, y_train)
- # 5、得出模型
- print("正规方程-权重系数为:\n", estimator.coef_)
- print("正规方程-偏置为:\n", estimator.intercept_)
- # 6、模型评估
- return None
- def linear2():
- """
- 梯度下降的优化方法对波士顿房价进行预测
- """
- # 1、获取数据
- boston = load_boston()
- # 2、划分数据集
- x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)
- # 3、标准化
- transfer = StandardScaler()
- x_train = transfer.fit_transform(x_train)
- x_test = transfer.transform(x_test)
- # 4、预估器
- estimator = SGDRegressor()
- estimator.fit(x_train, y_train)
- # 5、得出模型
- print("梯度下降-权重系数为:\n", estimator.coef_)
- print("梯度下降-偏置为:\n", estimator.intercept_)
- # 6、模型评估
- return None
- if __name__ == "__main__":
- # 代码1:正规方程的优化方法对波士顿房价进行预测
- linear1()
- # 代码2:梯度下降的优化方法对波士顿房价进行预测
- linear2()
运行结果:
- 正规方程-权重系数为:
- [-1.16537843 1.38465289 -0.11434012 0.30184283 -1.80888677 2.34171166
- 0.32381052 -3.12165806 2.61116292 -2.10444862 -1.80820193 1.19593811
- -3.81445728]
- 正规方程-偏置为:
- 21.93377308707127
- 梯度下降-权重系数为:
- [-1.10621345 1.29133856 -0.27846867 0.33474439 -1.69384501 2.4135466
- 0.29053621 -3.08390938 2.01002437 -1.44580391 -1.77085656 1.20016946
- -3.77661902]
- 梯度下降-偏置为:
- [21.9475731]
五、回归的性能评估
1、均方误差(Mean Squared Error)MSE评价机制

MSE 计算模型的预测值 Ŷ 与真实值 Y 的接近程度
2、sklearn.metrics.mean_squared_error(y_true, y_pred)
均方误差回归损失
y_true:真实值
y_pred:预测值
return:浮点数结果3、修改day03_machine_learning.py
- from sklearn.datasets import load_boston
- from sklearn.model_selection import train_test_split
- from sklearn.preprocessing import StandardScaler
- from sklearn.linear_model import LinearRegression, SGDRegressor
- from sklearn.metrics import mean_squared_error
- def linear1():
- """
- 正规方程的优化方法对波士顿房价进行预测
- """
- # 1、获取数据
- boston = load_boston()
- # 2、划分数据集
- x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)
- # 3、标准化
- transfer = StandardScaler()
- x_train = transfer.fit_transform(x_train)
- x_test = transfer.transform(x_test)
- # 4、预估器
- estimator = LinearRegression()
- estimator.fit(x_train, y_train)
- # 5、得出模型
- print("正规方程-权重系数为:\n", estimator.coef_)
- print("正规方程-偏置为:\n", estimator.intercept_)
- # 6、模型评估
- y_predict = estimator.predict(x_test)
- print("预测房价:\n", y_predict)
- error = mean_squared_error(y_test, y_predict)
- print("正规方程-均方误差为:\n", error)
- return None
- def linear2():
- """
- 梯度下降的优化方法对波士顿房价进行预测
- """
- # 1、获取数据
- boston = load_boston()
- # 2、划分数据集
- x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)
- # 3、标准化
- transfer = StandardScaler()
- x_train = transfer.fit_transform(x_train)
- x_test = transfer.transform(x_test)
- # 4、预估器
- estimator = SGDRegressor()
- estimator.fit(x_train, y_train)
- # 5、得出模型
- print("梯度下降-权重系数为:\n", estimator.coef_)
- print("梯度下降-偏置为:\n", estimator.intercept_)
- # 6、模型评估
- y_predict = estimator.predict(x_test)
- print("预测房价:\n", y_predict)
- error = mean_squared_error(y_test, y_predict)
- print("梯度下降-均方误差为:\n", error)
- return None
- if __name__ == "__main__":
- # 代码1:正规方程的优化方法对波士顿房价进行预测
- linear1()
- # 代码2:梯度下降的优化方法对波士顿房价进行预测
- linear2()
运行结果:
- 正规方程-权重系数为:
- [-1.16537843 1.38465289 -0.11434012 0.30184283 -1.80888677 2.34171166
- 0.32381052 -3.12165806 2.61116292 -2.10444862 -1.80820193 1.19593811
- -3.81445728]
- 正规方程-偏置为:
- 21.93377308707127
- 预测房价:
- [31.11439635 31.82060232 30.55620556 22.44042081 18.80398782 16.27625322
- 36.13534369 14.62463338 24.56196194 37.27961695 21.29108382 30.61258241
- 27.94888799 33.80697059 33.25072336 40.77177784 24.3173198 23.29773241
- 25.50732006 21.08959787 32.79810915 17.7713081 25.36693209 25.03811059
- 32.51925813 20.4761305 19.69609206 16.93696274 38.25660623 0.70152499
- 32.34837791 32.21000333 25.78226319 23.95722044 20.51116476 19.53727258
- 3.87253095 34.74724529 26.92200788 27.63770031 34.47281616 29.80511271
- 18.34867051 31.37976427 18.14935849 28.22386149 19.25418441 21.71490395
- 38.26297011 16.44688057 24.60894426 19.48346848 24.49571194 34.48915635
- 26.66802508 34.83940131 20.91913534 19.60460332 18.52442576 25.00178799
- 19.86388846 23.46800342 39.56482623 42.95337289 30.34352231 16.8933559
- 23.88883179 3.33024647 31.45069577 29.07022919 18.42067822 27.44314897
- 19.55119898 24.73011317 24.95642414 10.36029002 39.21517151 8.30743262
- 18.44876989 30.31317974 22.97029822 21.0205003 19.99376338 28.6475497
- 30.88848414 28.14940191 26.57861905 31.48800196 22.25923033 -5.35973252
- 21.66621648 19.87813555 25.12178903 23.51625356 19.23810222 19.0464234
- 27.32772709 21.92881244 26.69673066 23.25557504 23.99768158 19.28458259
- 21.19223276 10.81102345 13.92128907 20.8630077 23.40446936 13.91689484
- 28.87063386 15.44225147 15.60748235 22.23483962 26.57538077 28.64203623
- 24.16653911 18.40152087 15.94542775 17.42324084 15.6543375 21.04136264
- 33.21787487 30.18724256 20.92809799 13.65283665 16.19202962 29.25155603
- 13.28333127]
- 正规方程-均方误差为:
- 32.44253669600673
- 梯度下降-权重系数为:
- [-1.10720669 1.25231283 -0.31509564 0.34535296 -1.64340471 2.45533074
- 0.24591813 -3.00623279 1.86680194 -1.35635736 -1.75927819 1.21751662
- -3.75820164]
- 梯度下降-偏置为:
- [21.93446341]
- 预测房价:
- [30.5553054 31.9029657 30.49644841 23.21944515 18.96884856 16.18632636
- 36.24105194 14.87804697 24.3895523 37.20352522 21.5386604 30.60951187
- 27.65148152 33.50851129 33.21249389 40.83380512 24.46605375 22.88832148
- 25.52501927 21.58868475 32.80656665 17.73245419 25.66824551 25.08604864
- 32.97047549 20.30353258 19.68164294 16.91361879 38.1855976 0.27760932
- 32.54896674 32.02576312 25.94574949 23.97039625 20.35535178 19.78087986
- 3.89351738 34.35969722 26.90276862 27.75996947 34.54094573 29.54994096
- 18.27465483 31.39534921 18.00180158 28.4390917 19.23254806 21.52452332
- 37.97845293 16.57097091 24.5471993 19.39657317 24.21252437 34.9227855
- 26.80416589 34.74661413 21.23727026 19.59775567 18.39910461 25.0523942
- 20.19548887 23.82772896 40.02092877 43.04844803 30.42801759 17.20699337
- 23.93074887 3.06161671 31.11592258 29.56981815 18.4009017 27.37058447
- 19.36967055 24.60927521 25.32075297 10.35369309 39.25900753 8.1790075
- 18.11059373 30.75396941 22.93518314 21.69853793 20.21950513 28.49235921
- 31.07597036 28.29348444 26.43666514 31.70687029 22.21769412 -5.45800192
- 21.63087532 19.7545147 25.08781498 23.61546397 18.84729974 19.10306716
- 27.25447935 22.00263139 26.57769298 23.53325788 23.87869699 19.51281905
- 21.00527045 10.1261844 14.03654344 21.12885311 23.21744834 15.17783691
- 28.87985666 15.68906271 15.61491721 22.063714 26.98392894 28.64368984
- 24.01307784 18.36664466 15.87301799 17.66160742 15.84512198 20.84217027
- 33.17275758 30.60002844 21.15789543 14.11621048 16.30693791 29.17718858
- 13.16315128]
- 梯度下降-均方误差为:
- 32.55418193625462
六、正规方程和梯度下降对比
1、对比
梯度下降 正规方程 需要选择学习率 不需要 需要迭代求解 一次运算得出 特征数量较大可以使用 需要计算方程,时间复杂度高O(n3) 2、选择
小规模数据:
LinearRegression(不能解决拟合问题)
岭回归
大规模数据:
SGDRegressor七、梯度下降预估器优化方法-GD、SGD、SAG
1、GD
梯度下降(Gradient Descent),原始的梯度下降法需要计算所有样本的值才能够得出梯度,计算量大,所以后面才有会一系列的改进2、SGD
随机梯度下降(Stochastic gradient descent)是一个优化方法。它在一次迭代时只考虑一个训练样本SGD的优点是:
高效
容易实现SGD的缺点是:
SGD需要许多超参数:比如正则项参数、迭代数
SGD对于特征标准化是敏感的3、SAG
随机平均梯度法(Stochasitc Average Gradient),由于收敛的速度太慢,有人提出SAG等基于梯度下降的算法Scikit-learn:SGDRegressor、岭回归、逻辑回归等当中都会有SAG优化
-
相关阅读:
pair的基本用法总结
Java+JSP+Mysql+Tomcat实现Web图书管理系统
awk的简单使用
Idea汉化
java版工程管理系统Spring Cloud+Spring Boot+Mybatis实现工程管理系统源码
Android开发之——Jetpack Compose手势与交互(9)
springboot+人力资源管理系统 毕业设计-附源码181614
腾讯云 jar项目配置【半小时完成】(Spring boot Mysql)
【用户画像】ClickHouse中的数据类型、表引擎介绍及使用、项目几个问题的解决办法
企业级数据中台应用架构和技术架构
- 原文地址:https://blog.csdn.net/csj50/article/details/133610626
