计算机竞赛 题目：基于卷积神经网络的手写字符识别 - 深度学习

0 前言

🔥 优质竞赛项目系列，今天要分享的是

基于卷积神经网络的手写字符识别

该项目较为新颖，适合作为竞赛课题方向，学长非常推荐！

🧿 更多资料, 项目分享：

https://gitee.com/dancheng-senior/postgraduate

1 简介

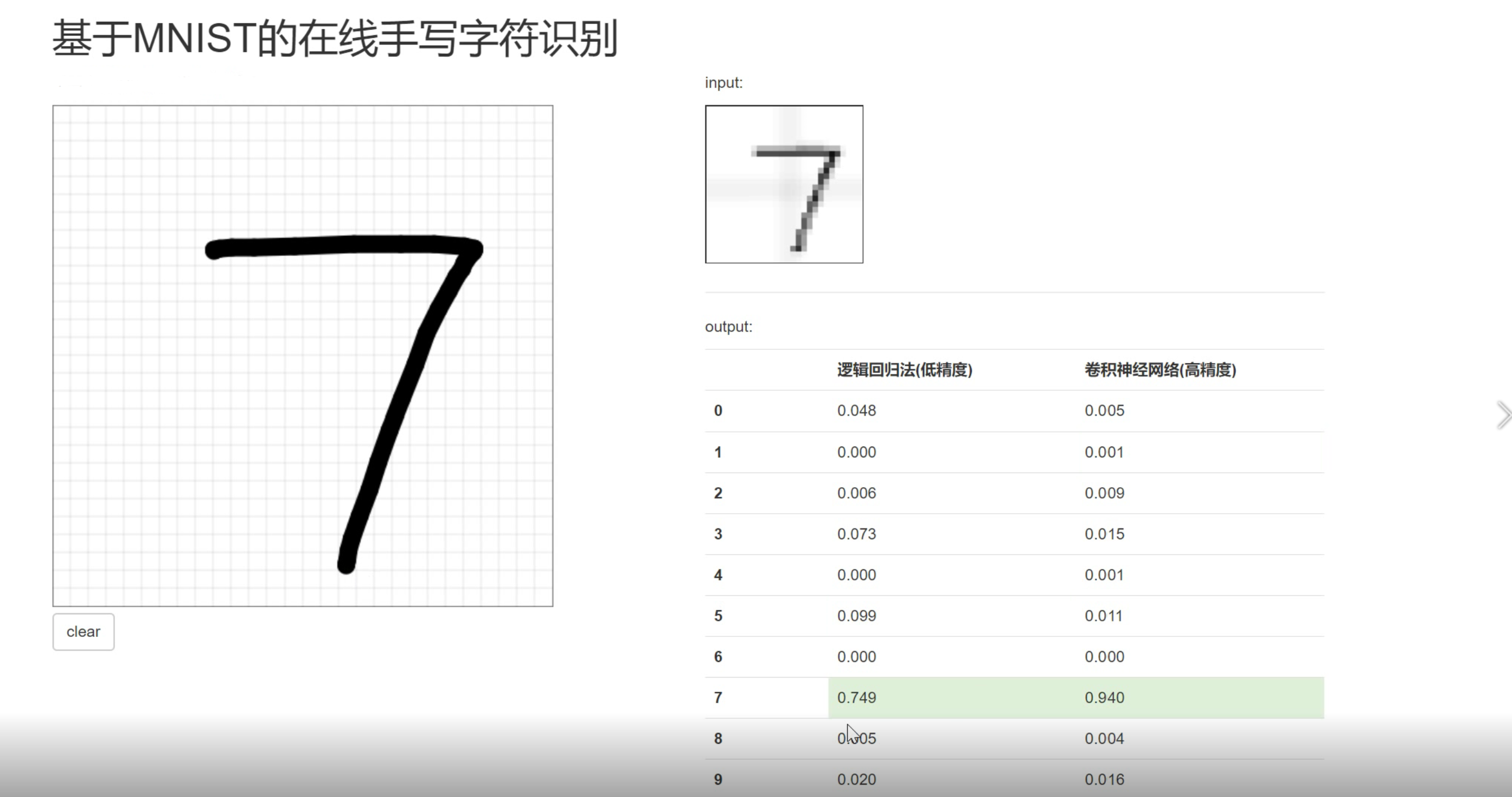
该设计学长使用python基于TensorFlow设计手写数字识别算法，并编程实现GUI界面，构建手写数字识别系统。

这是学长做的深度学习demo，大家可以用于竞赛课题。

这里学长不会以论文的形式展现，而是以编程实战完成深度学习项目的角度去描述。

项目要求：主要解决的问题是手写数字识别，最终要完成一个识别系统。

设计识别率高的算法，实现快速识别的系统。

2 LeNet-5 模型的介绍

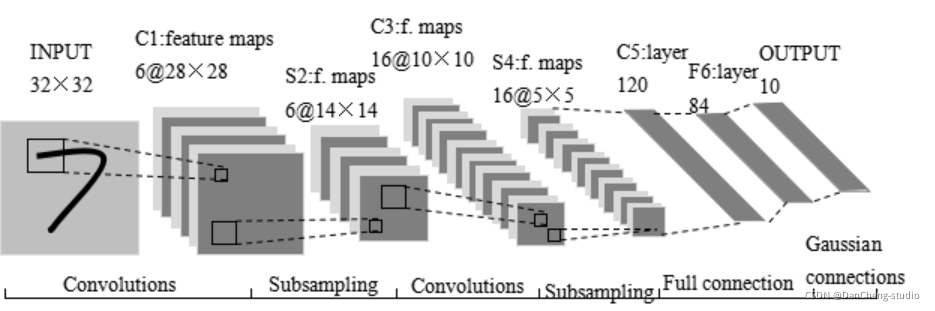
学长实现手写数字识别，使用的是卷积神经网络，建模思想来自LeNet-5，如下图所示：

2.1 结构解析

这是原始的应用于手写数字识别的网络，我认为这也是最简单的深度网络。

LeNet-5不包括输入，一共7层，较低层由卷积层和最大池化层交替构成，更高层则是全连接和高斯连接。

LeNet-5的输入与BP神经网路的不一样。这里假设图像是黑白的，那么LeNet-5的输入是一个32*32的二维矩阵。同
时，输入与下一层并不是全连接的，而是进行稀疏连接。本层每个神经元的输入来自于前一层神经元的局部区域(5×5)，卷积核对原始图像卷积的结果加上相应的阈值，得出的结果再经过激活函数处理，输出即形成卷积层（C层）。卷积层中的每个特征映射都各自共享权重和阈值，这样能大大减少训练开销。降采样层（S层）为减少数据量同时保存有用信息，进行亚抽样。

2.2 C1层

第一个卷积层（C1层）由6个特征映射构成，每个特征映射是一个28×28的神经元阵列，其中每个神经元负责从5×5的区域通过卷积滤波器提取局部特征。一般情况下，滤波器数量越多，就会得出越多的特征映射，反映越多的原始图像的特征。本层训练参数共6×(5×5+1)=156个，每个像素点都是由上层5×5=25个像素点和1个阈值连接计算所得，共28×28×156=122304个连接。

2.3 S2层

S2层是对应上述6个特征映射的降采样层（pooling层）。pooling层的实现方法有两种，分别是max-pooling和mean-
pooling，LeNet-5采用的是mean-
pooling，即取n×n区域内像素的均值。C1通过2×2的窗口区域像素求均值再加上本层的阈值，然后经过激活函数的处理，得到S2层。pooling的实现，在保存图片信息的基础上，减少了权重参数，降低了计算成本，还能控制过拟合。本层学习参数共有1*6+6=12个，S2中的每个像素都与C1层中的2×2个像素和1个阈值相连，共6×(2×2+1)×14×14=5880个连接。

S2层和C3层连接

S2层和C3层的连接比较复杂。C3卷积层是由16个大小为10×10的特征映射组成的，当中的每个特征映射与S2层的若干个特征映射的局部感受野（大小为5×5）相连。其中，前6个特征映射与S2层连续3个特征映射相连，后面接着的6个映射与S2层的连续的4个特征映射相连，然后的3个特征映射与S2层不连续的4个特征映射相连，最后一个映射与S2层的所有特征映射相连。

此处卷积核大小为5×5，所以学习参数共有6×(3×5×5+1)+9×(4×5×5+1)+1×(6×5×5+1)=1516个参数。而图像大小为28×28，因此共有151600个连接。

S4层是对C3层进行的降采样，与S2同理，学习参数有16×1+16=32个，同时共有16×(2×2+1)×5×5=2000个连接。
C5层是由120个大小为1×1的特征映射组成的卷积层，而且S4层与C5层是全连接的，因此学习参数总个数为120×(16×25+1)=48120个。

2.4 F6与C5层

F6是与C5全连接的84个神经元，所以共有84×(120+1)=10164个学习参数。

卷积神经网络通过通过稀疏连接和共享权重和阈值，大大减少了计算的开销，同时，pooling的实现，一定程度上减少了过拟合问题的出现，非常适合用于图像的处理和识别。

3 写数字识别算法模型的构建

3.1 输入层设计

输入为28×28的矩阵，而不是向量。

3.2 激活函数的选取

Sigmoid函数具有光滑性、鲁棒性和其导数可用自身表示的优点，但其运算涉及指数运算，反向传播求误差梯度时，求导又涉及乘除运算，计算量相对较大。同时，针对本文构建的含有两层卷积层和降采样层，由于sgmoid函数自身的特性，在反向传播时，很容易出现梯度消失的情况，从而难以完成网络的训练。因此，本文设计的网络使用ReLU函数作为激活函数。

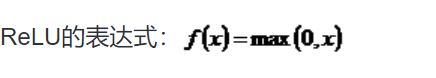
3.3 卷积层设计

学长设计卷积神经网络采取的是离散卷积，卷积步长为1，即水平和垂直方向每次运算完，移动一个像素。卷积核大小为5×5。

3.4 降采样层

学长设计的降采样层的pooling方式是max-pooling，大小为2×2。

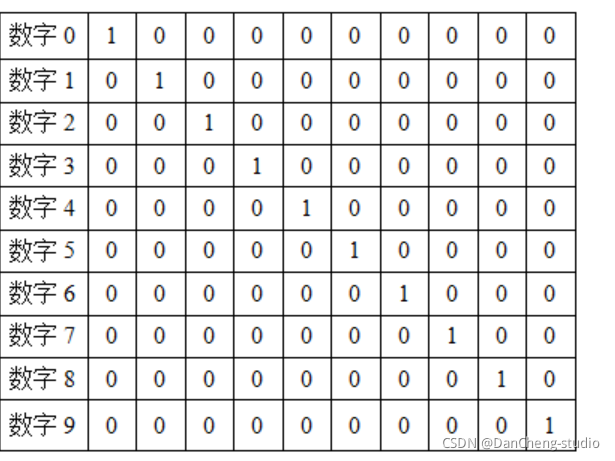
3.5 输出层设计

输出层设置为10个神经网络节点。数字0~9的目标向量如下表所示：

4 网络模型的总体结构

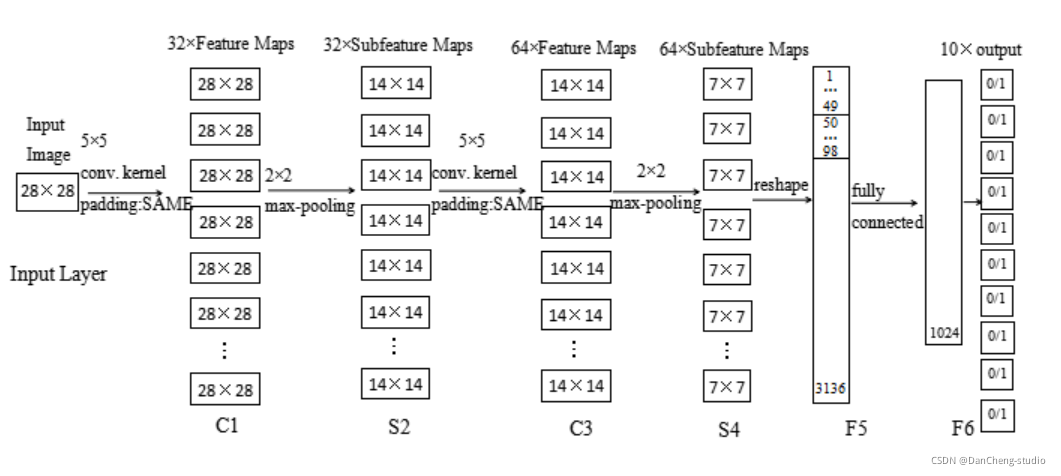
5 部分实现代码

使用Python，调用TensorFlow的api完成手写数字识别的算法。

注：我的程序运行环境是：Win10,python3.。

当然，也可以在Linux下运行，由于TensorFlow对py2和py3兼容得比较好，在Linux下可以在python2.7中运行。

​

    #!/usr/bin/env python2
    # -*- coding: utf-8 -*-
   
    #import modules
    import numpy as np
    import matplotlib.pyplot as plt
    #from sklearn.metrics import confusion_matrix
    import tensorflow as tf
    import time
    from datetime import timedelta
    import math
    from tensorflow.examples.tutorials.mnist import input_data

    def new_weights(shape):
      return tf.Variable(tf.truncated_normal(shape,stddev=0.05))
    def new_biases(length):
      return tf.Variable(tf.constant(0.1,shape=length))
    def conv2d(x,W):
      return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')
    def max_pool_2x2(inputx):
      return tf.nn.max_pool(inputx,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
    
    #import data
    data = input_data.read_data_sets("./data", one_hot=True) # one_hot means [0 0 1 0 0 0 0 0 0 0] stands for 2
    
    print("Size of:")
    print("--Training-set:\t\t{}".format(len(data.train.labels)))
    print("--Testing-set:\t\t{}".format(len(data.test.labels)))
    print("--Validation-set:\t\t{}".format(len(data.validation.labels)))
    data.test.cls = np.argmax(data.test.labels,axis=1)  # show the real test labels: [7 2 1 ..., 4 5 6], 10000values
    
    x = tf.placeholder("float",shape=[None,784],name='x')
    x_image = tf.reshape(x,[-1,28,28,1])
    
    y_true = tf.placeholder("float",shape=[None,10],name='y_true')
    y_true_cls = tf.argmax(y_true,dimension=1)
    # Conv 1
    layer_conv1 = {"weights":new_weights([5,5,1,32]),
            "biases":new_biases([32])}
    h_conv1 = tf.nn.relu(conv2d(x_image,layer_conv1["weights"])+layer_conv1["biases"])
    h_pool1 = max_pool_2x2(h_conv1)
    # Conv 2
    layer_conv2 = {"weights":new_weights([5,5,32,64]),
            "biases":new_biases([64])}
    h_conv2 = tf.nn.relu(conv2d(h_pool1,layer_conv2["weights"])+layer_conv2["biases"])
    h_pool2 = max_pool_2x2(h_conv2)
    # Full-connected layer 1
    fc1_layer = {"weights":new_weights([7*7*64,1024]),
          "biases":new_biases([1024])}
    h_pool2_flat = tf.reshape(h_pool2,[-1,7*7*64])
    h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,fc1_layer["weights"])+fc1_layer["biases"])
    # Droupout Layer
    keep_prob = tf.placeholder("float")
    h_fc1_drop = tf.nn.dropout(h_fc1,keep_prob)
    # Full-connected layer 2
    fc2_layer = {"weights":new_weights([1024,10]),
           "biases":new_weights([10])}
    # Predicted class
    y_pred = tf.nn.softmax(tf.matmul(h_fc1_drop,fc2_layer["weights"])+fc2_layer["biases"]) # The output is like [0 0 1 0 0 0 0 0 0 0]
    y_pred_cls = tf.argmax(y_pred,dimension=1) # Show the real predict number like '2'
    # cost function to be optimized
    cross_entropy = -tf.reduce_mean(y_true*tf.log(y_pred))
    optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(cross_entropy)
    # Performance Measures
    correct_prediction = tf.equal(y_pred_cls,y_true_cls)
    accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))
    with tf.Session() as sess:
      init = tf.global_variables_initializer()
      sess.run(init)
      train_batch_size = 50
      def optimize(num_iterations):
        total_iterations=0
        start_time = time.time()
        for i in range(total_iterations,total_iterations+num_iterations):
          x_batch,y_true_batch = data.train.next_batch(train_batch_size)
          feed_dict_train_op = {x:x_batch,y_true:y_true_batch,keep_prob:0.5}
          feed_dict_train = {x:x_batch,y_true:y_true_batch,keep_prob:1.0}
          sess.run(optimizer,feed_dict=feed_dict_train_op)
          # Print status every 100 iterations.
          if i%100==0:
            # Calculate the accuracy on the training-set.
            acc = sess.run(accuracy,feed_dict=feed_dict_train)
            # Message for printing.
            msg = "Optimization Iteration:{0:>6}, Training Accuracy: {1:>6.1%}"
            # Print it.
            print(msg.format(i+1,acc))
        # Update the total number of iterations performed
        total_iterations += num_iterations
        # Ending time
        end_time = time.time()
        # Difference between start and end_times.
        time_dif = end_time-start_time
        # Print the time-usage
        print("Time usage:"+str(timedelta(seconds=int(round(time_dif)))))
      test_batch_size = 256
      def print_test_accuracy():
        # Number of images in the test-set.
        num_test = len(data.test.images)
        cls_pred = np.zeros(shape=num_test,dtype=np.int)
        i = 0
        while i < num_test:
          # The ending index for the next batch is denoted j.
          j = min(i+test_batch_size,num_test)
          # Get the images from the test-set between index i and j
          images = data.test.images[i:j, :]
          # Get the associated labels
          labels = data.test.labels[i:j, :]
          # Create a feed-dict with these images and labels.
          feed_dict={x:images,y_true:labels,keep_prob:1.0}
          # Calculate the predicted class using Tensorflow.
          cls_pred[i:j] = sess.run(y_pred_cls,feed_dict=feed_dict)
          # Set the start-index for the next batch to the
          # end-index of the current batch
          i = j
        cls_true = data.test.cls
        correct = (cls_true==cls_pred)
        correct_sum = correct.sum()
        acc = float(correct_sum) / num_test
        # Print the accuracy
        msg = "Accuracy on Test-Set: {0:.1%} ({1}/{2})"
        print(msg.format(acc,correct_sum,num_test))
      # Performance after 10000 optimization iterations
      optimize(num_iterations=10000)
      print_test_accuracy()
      savew_hl1 = layer_conv1["weights"].eval()
      saveb_hl1 = layer_conv1["biases"].eval()
      savew_hl2 = layer_conv2["weights"].eval()
      saveb_hl2 = layer_conv2["biases"].eval()
      savew_fc1 = fc1_layer["weights"].eval()
      saveb_fc1 = fc1_layer["biases"].eval()
      savew_op = fc2_layer["weights"].eval()
      saveb_op = fc2_layer["biases"].eval()
    
      np.save("savew_hl1.npy", savew_hl1)
      np.save("saveb_hl1.npy", saveb_hl1)
      np.save("savew_hl2.npy", savew_hl2)
      np.save("saveb_hl2.npy", saveb_hl2)
      np.save("savew_hl3.npy", savew_fc1)
      np.save("saveb_hl3.npy", saveb_fc1)
      np.save("savew_op.npy", savew_op)
      np.save("saveb_op.npy", saveb_op)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

运行结果显示：测试集中准确率大概为99.2%。

查看混淆矩阵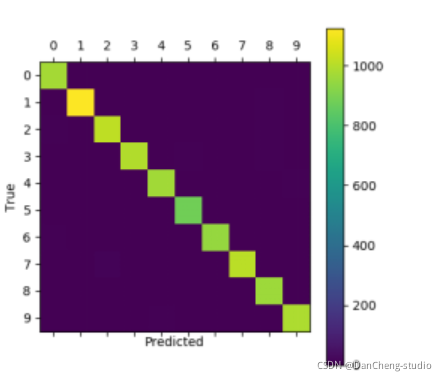

6 在线手写识别

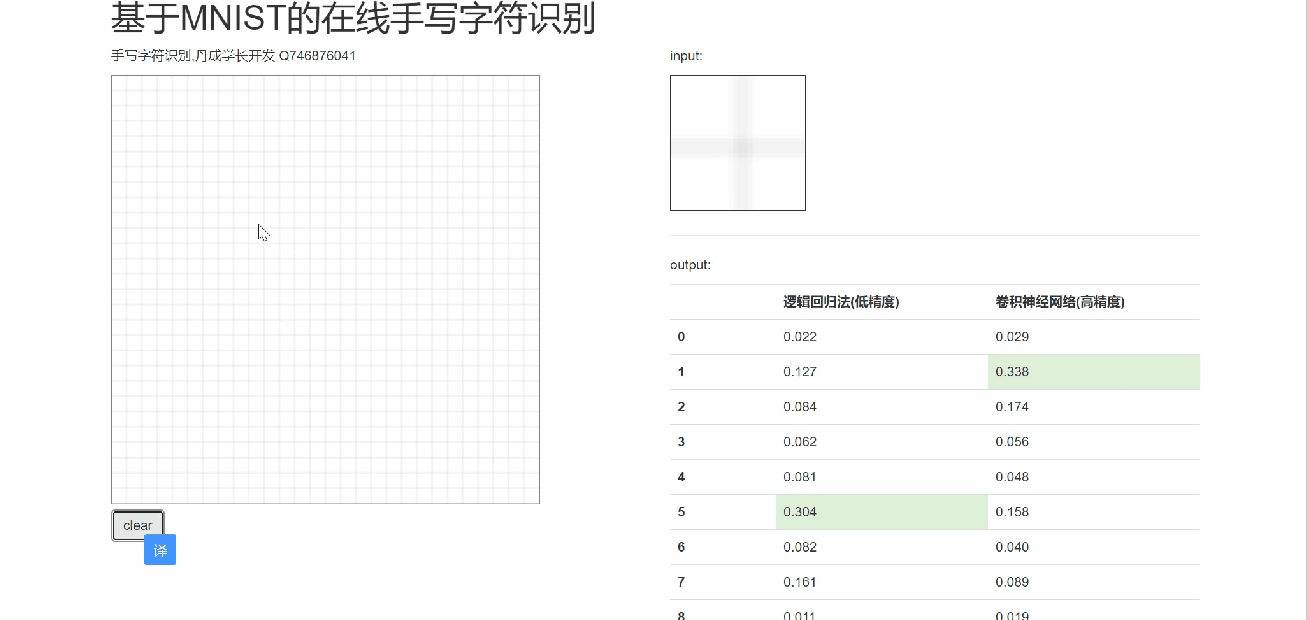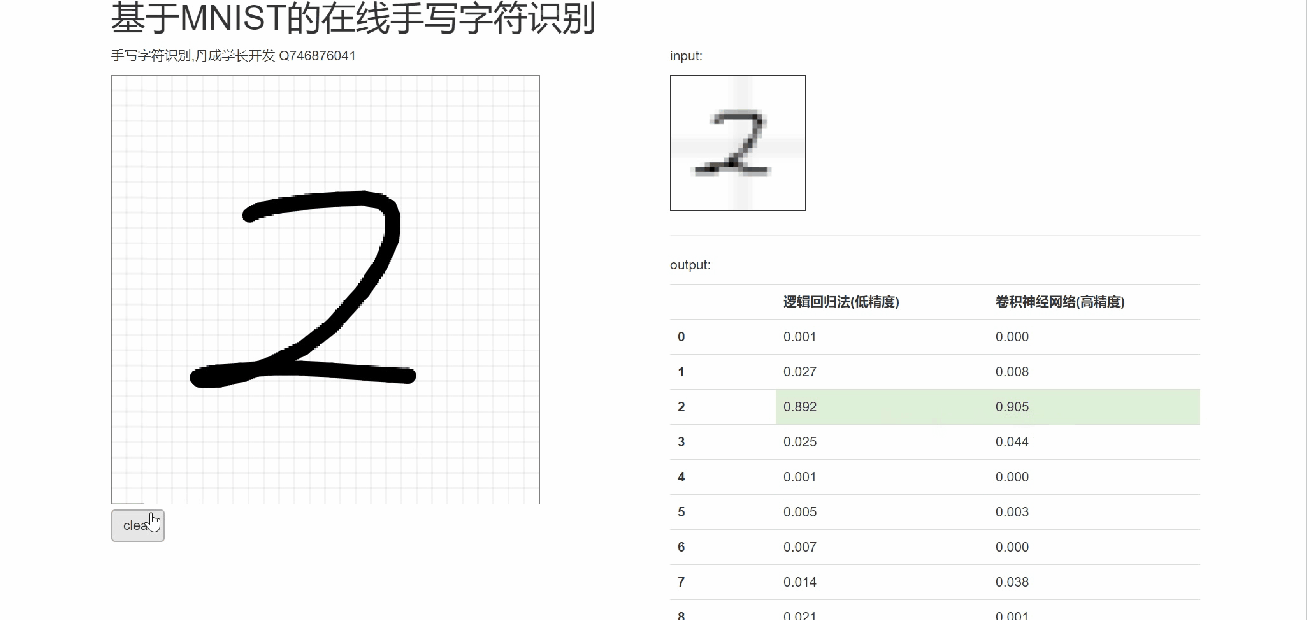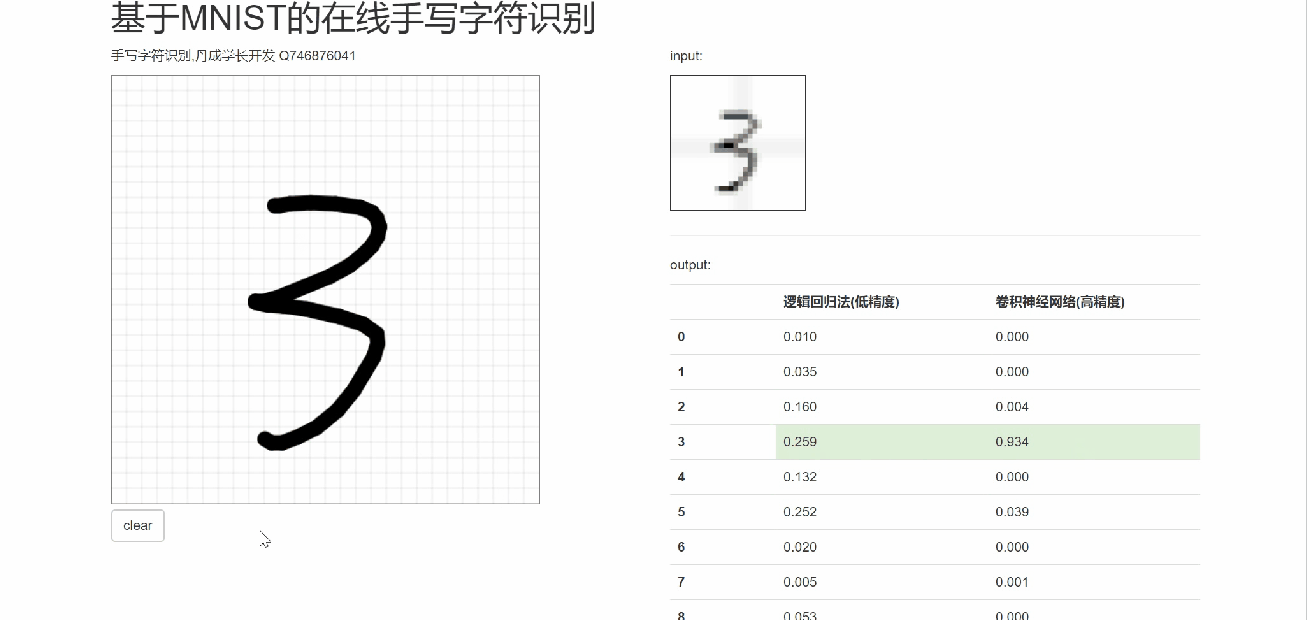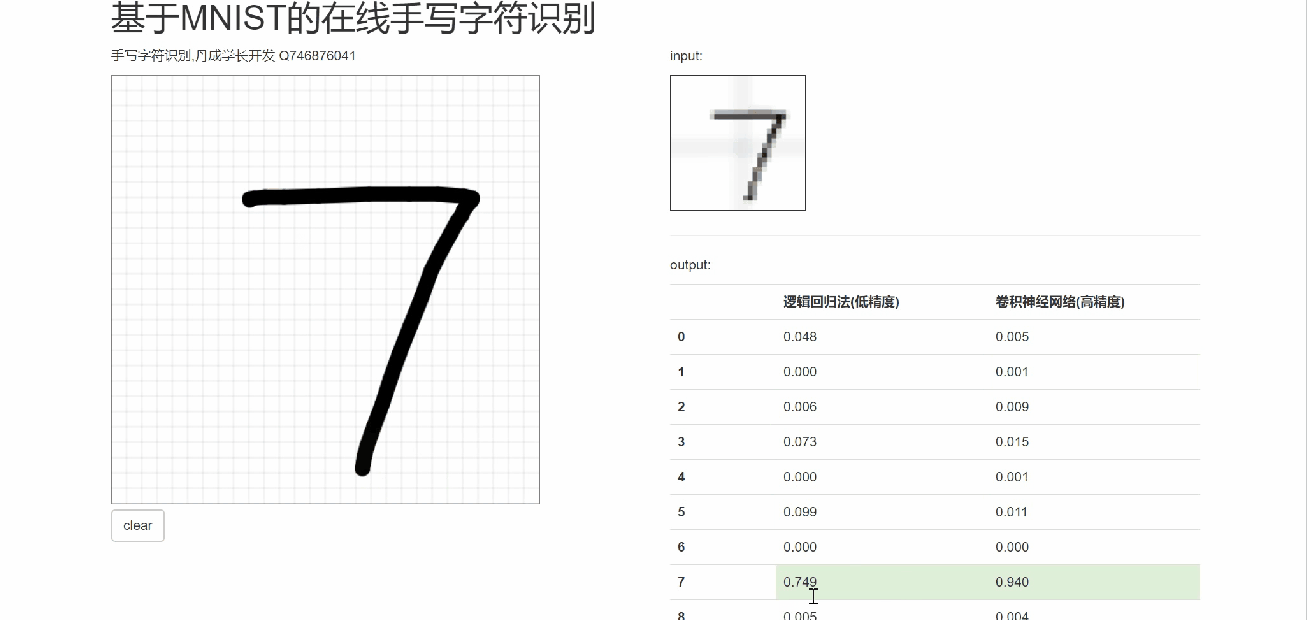
7 最后

🧿 更多资料, 项目分享：

https://gitee.com/dancheng-senior/postgraduate