代码随想录算法训练营第五十九天 | 647. 回文子串 & 516.最长回文子序列

1. 回文子串 

647. 回文子串 - 力扣（LeetCode）

一个子串左右两个元素相等，并且中间对称，才是回文子串

即 i=j 时，[i+1: j-1]对称

dp[i][j]： [i:j] 是否是回文字串

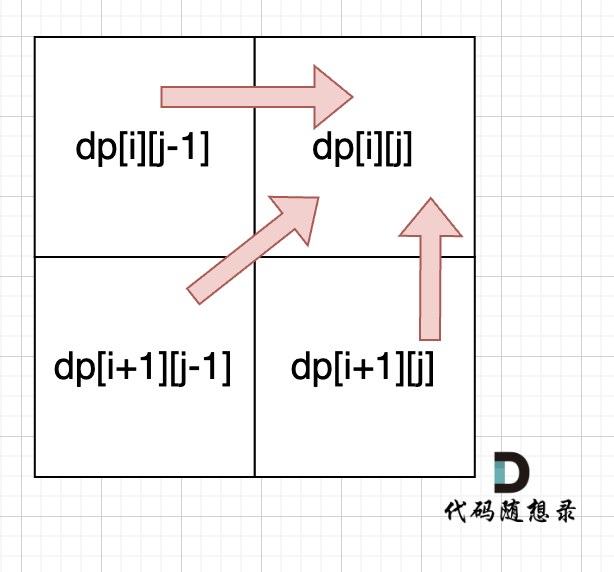
当 子串长度大于2 由 dp[i+1][j-1] 推出， i 由 i+1推出 所以 i 要倒序

不大于2时，则由 i j 决定

class Solution {
    public int countSubstrings(String s) {
        int length = s.length();
        boolean dp[][] = new boolean[length][length];
        // dp[i][j] [i:j] 是否是回文字串
 
        int res = 0;
        for(int i = length-1; i > -1; i--){
            for(int j = i; j < length; j++){
                if(s.charAt(i) == s.charAt(j)){
                    if(j-i <= 1){ // 字串长度不超过2
                        dp[i][j] = true;
                        res++;
                    }else if(dp[i+1][j-1]){
                        dp[i][j] = true;
                        res++;
                    }
                }
            }
        }
        return res;
    }
}

 

2. 最长回文子序列

516. 最长回文子序列 - 力扣（LeetCode）

子序列可以不连续 所以当 s[i] != s[j] 也需要考虑

s[i] == s[j] 时，中间的长度 + 2

s[i] != s[j] 时，要考虑左右两个哪个加入中间后更长

class Solution {
    public int longestPalindromeSubseq(String s) {
        int length = s.length();
        int[][] dp = new int[length][length];
 
        for(int i = length-1; i > -1; i--){
            dp[i][i] = 1; // 字串长度为 1 必然相等
            for(int j = i + 1; j < length; j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2; // dp[1][2] = dp[2][1] + 2 = 0 + 2
                }else{
                    dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][length-1];
    }
}