【计算机组成原理】考研真题攻克与重点知识点剖析 - 第 2 篇：数据的表示和运算

前言

• 本文基础知识部分来自于b站：分享笔记的好人儿的思维导图与王道考研课程，感谢大佬的开源精神，习题来自老师划的重点以及考研真题。
• 此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析，本人技术有限，最终数据清洗结果不够理想，相关CSDN文章便没有发出。
• 这里我将按章节顺序，围绕考研真题展开计算机组成原理总共7章的知识,边学习边整理数据。
• 第一章链接：【计算机组成原理】考研真题攻克与重点知识点剖析 - 第 1 篇：计算机系统概述

请注意，本文中的部分内容来自网络搜集和个人实践，如有任何错误，请随时向我们提出批评和指正。本文仅供学习和交流使用，不涉及任何商业目的。如果因本文内容引发版权或侵权问题，请通过私信告知我们，我们将立即予以删除。

数据的表示

数制与编码

• 真值与机器数

  • 机器数：用0和1编码的计算机内部的0/1序列

  • 真值：机器数代表的实际值，现实中带正负号的数，X

• 数值数据表示的三要素（要确定一个数值数据的值必须先确定这三个要素）

  • 进位计数制

    • 十进制（后缀D）、二进制（后缀B）、十六进制（后缀H，或前缀0x表示）、八进制（后缀O）

  • 定/浮点表示

    • 浮点整数、定点小数、浮点数（解决小数点问题）

  • 二进制编码

    • 原码、补码、反码、移码（解决正负号问题）

• 十进制数与R进制数之间的转换

  • R进制到十进制（按“权”展开）
    

  • 十进制到二进制，再将二进制转十六（四位一组）或八进制（三位一组）
    
    

  • 二进制<–>八进制、十六进制

• 各种进制的常见书写方式
  

真值和机器数定义

以上知识思维导图

可跳过

BCD码

无符号整数运算

有符号整数运算

原码表示

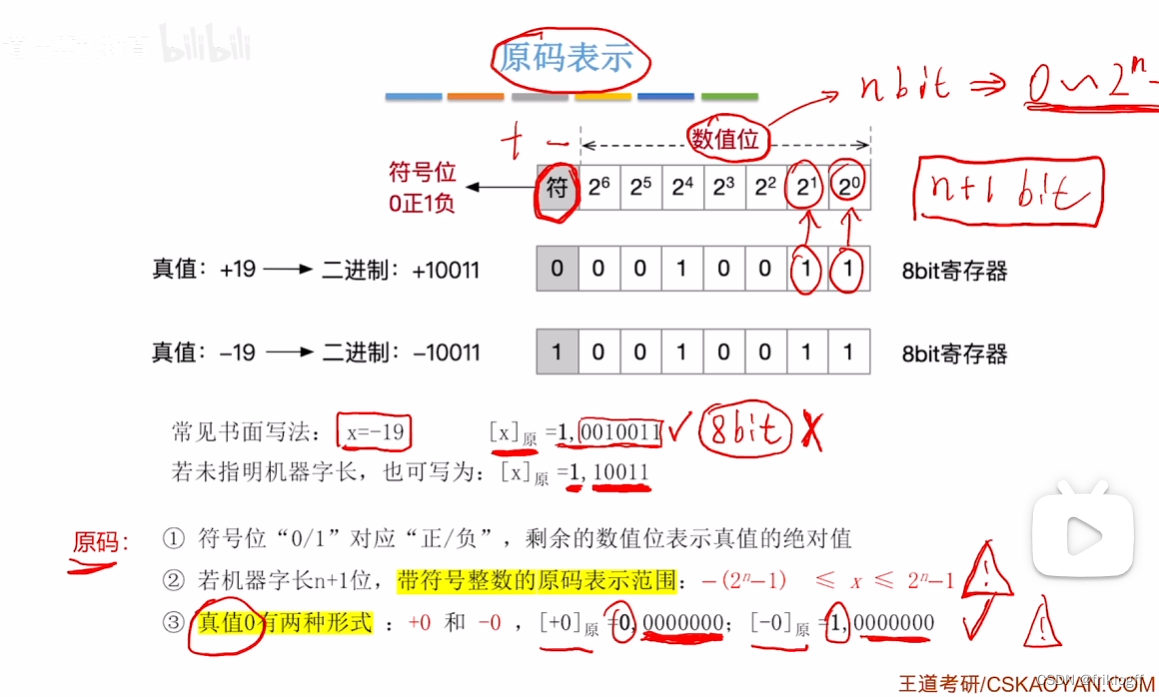
源码缺点

原码→反码→补码的转换（机算)

原码、补码快速转换技巧(手算)

补码的加法运算（例1)

19=16+2+1
0001 0011

补码的加法运算（例2)

移码

练习

以上知识总结

数据存储时的字节排列

• 大端方式：从最高有效字节到最低有效字节的顺序存储数据（从左到右，正常思维）

• 小端方式：从最低有效字节到最高有效字节的顺序存储数据（从右到左，便于机器）
  

• 边界对齐问题：存储数据不满字长，填充空白，虽然浪费空间，但提高效率（若数据不对齐可能额外存取一次）

• 

机器数表示方法

定点数

定点::小数点位置固定

定点数的表示

• 原码

  • 最高位为符号位，数值部分不变

• 补码

  • 定义：[X]补 = 2^n + X（-2^n <= X < 2^n，mod 2^n）

  • 理解：为了机器数加减运算的统一。
    实际上是模运算，一个负数的补码等于模减该负数的绝对值，即时钟从10点到6点，可以倒拨4格：10-4=6；也可以顺拨8格，10+8=18=6

• 反码

  • 原码与补码相互转化的过渡

• 移码

  • 数值加一个偏置常数，通常在真值X上加2^n（便于浮点数加减运算时对阶，阶数有正有负，统一加一个常数让阶数都为正方便比较）

• 不同机器数之间的转换关系
  

• 范围与真值0

  • 定点整数

    • 原码

      • 范围：- (2^n - 1) <= x <= 2^n - 1

        • 最大：0,111…111

          • 最小：1,111…111

            • 真值零: 0,000…000，1,000…000

    • 反码

      • 范围：- (2^n - 1) <= x <= 2^n - 1

        • 最大：0,111…111

          • 最小：1,000…000

            • 真值零: 0,000…000，1,111…111

    • 补码

      • 范围：- 2^n <= x <= 2^n - 1

        • 最大：0,111…111

          • 最小：1,000…000

            • 真值零: 0,000…000

  • 定点小数

    • 原码

      • 范围：- (1 - 2^-n) <= x <= 1 - 2^-n

        • 最大：0,111…111

          • 最小：1,111…111

            • 真值零: 0,000…000，1,000…000

    • 反码

      • 范围：- (1 - 2^-n) <= x <= 1 - 2^-n

        • 最大：0,111…111

          • 最小：1,000…000

            • 真值零: 0,000…000，1,111…111

    • 补码

      • 范围：-1 <= x <= 1 - 2^-n

        • 最大：0,111…111

          • 最小：1,000…000

            • 真值零: 0,000…000

• 有符号数与无符号数

  • 有符号数：最高位的0/1表示正/负

  • 无符号数：整个机器字长全部二进制位均为数值位，无符号位

  • 同时有无符号数和带符号数，在C编译器中隐含将带符号整数强制转换为无符号数

定点小数vs定点整数

（+/-）0/1 000 0001.
（+/-）0/1. 000 0001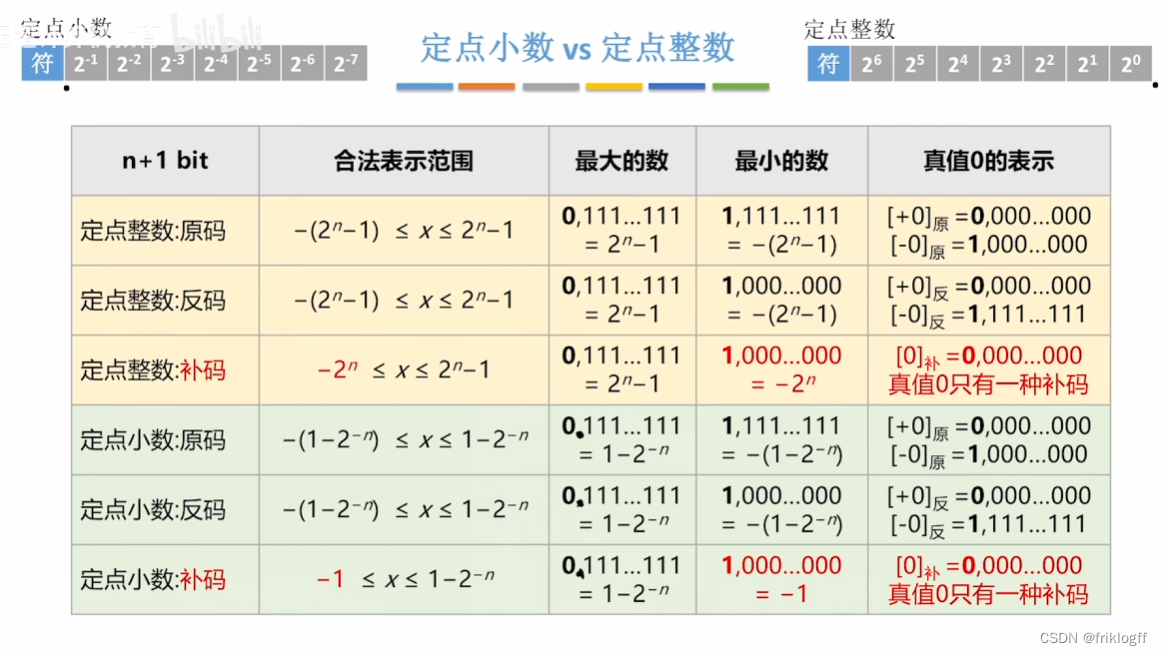

定点数的局限性

浮点数

浮点数的表示（约定小数点位置）

• 一般格式

  • 浮点数真值格式：N = r^E × M（r阶码的底，E阶码用移码表示，M尾数，S数符）

  • 表示范围（原码对称，故表示范围关于原点对称）

  • 浮点数范围比定点数大，但个数不变，故数更稀疏且不均匀

• 规格化浮点数

  • 规格化数形式：+/-1.M × r^E

    • 为了表示更多有效数字，规定规格化数的小数点前为1

  • 基数2：原码规格化最高位一定是1，补码规格化数的尾数最高位一定与尾数符号相反（基数4原码最高两位不全为0，基数8原码最高三位不全为0）

• IEEE754标准

  • +/-1.M × 2^E（S数符，E阶码用移码表示全0全1特殊表示，M(Significand)尾数用原码表示，隐含尾数最高数位）

  • 短浮点数

    • 数符1+阶码8+尾数23=总位数32（偏置值127）

      • 范围：1 × 2^(1-127) ---------- 1.111…111 × 2^(254-127)

  • 长浮点数

    • 数符1+阶码11+尾数52=总位数64（偏置值1023）

      • 范围：1 × 2^(1-1023) ---------- 1.111…111 × 2^(2046-1023)

  • 特殊数的表示

    • 阶码全0，尾数M=0，真值X=0+(0-)

    • 阶码全0，尾数M!=0，非规格化小数

    • 阶码全1，尾数M=0，真值X=+∞(-无穷)

    • 阶码全1，尾数M!=0，非数值NaN

浮点数尾数的规格化

浮点数的表示思维导图

IEEE 754标准

偏置值-1

• 关于-1000 0000+0111 1111 = 1111 1111

2^8=1 0000 0000 任何运算结果在mod2的8次方后，都只会保留最低的八位，
所以在这里我们可以 将 0111 1111+1 0000 0000=1 0111 1111，
这样就使 被减数 比 减数 大 1 0111 1111-1000 0000 = 1111 1111

例1

例2

例3

数据的运算

布尔代数和基本逻辑电路

• 基本逻辑运算：与或非，任何逻辑表达式可写成三种基本运算的逻辑组合

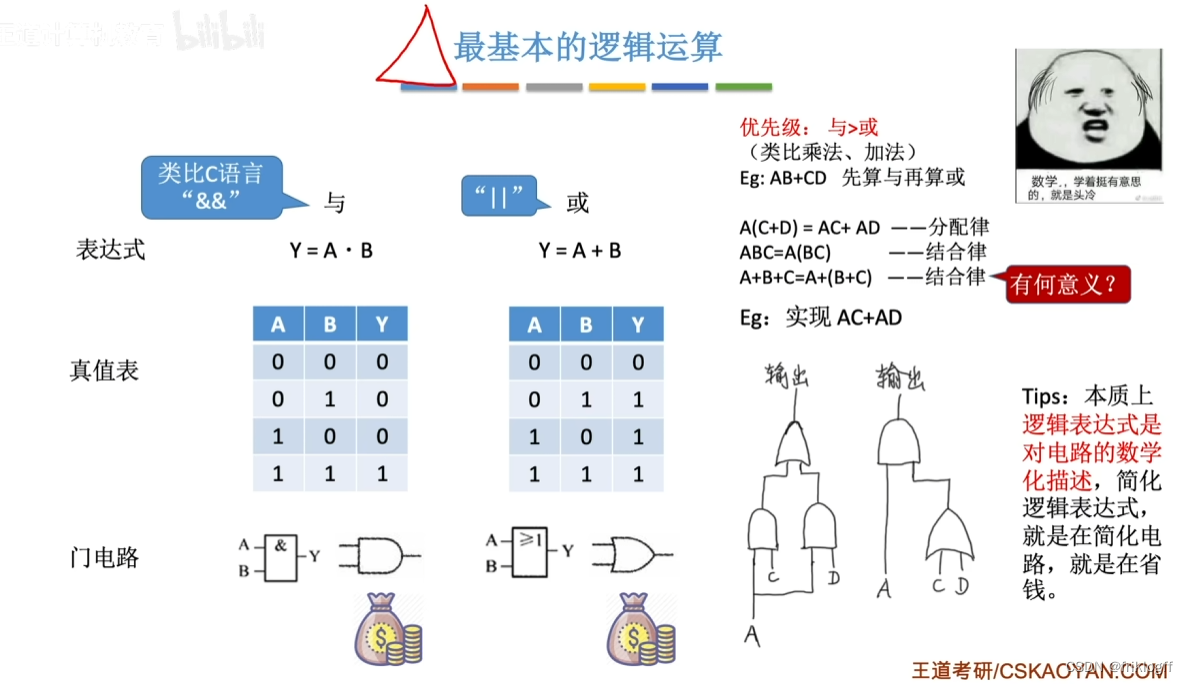
• 组合逻辑电路：没有存储功能，输出仅依赖于当前输入

• 具有存储功能，其输出不仅依赖于当前输入，还依赖于存储单元当前状态

• 组合逻辑部件（功能部件，利用基本逻辑门电路构成）：译码器、编码器、多路选择器、加法器

加法器（所有算数运算部件都基于加法器）

加法器原理

补码加减运算器(利用加法器实现)

计算有符号数

sub=0

sub=1

计算无符号数

电路相同，判断溢出方式不同
sub=0

sub=1

标志位生成

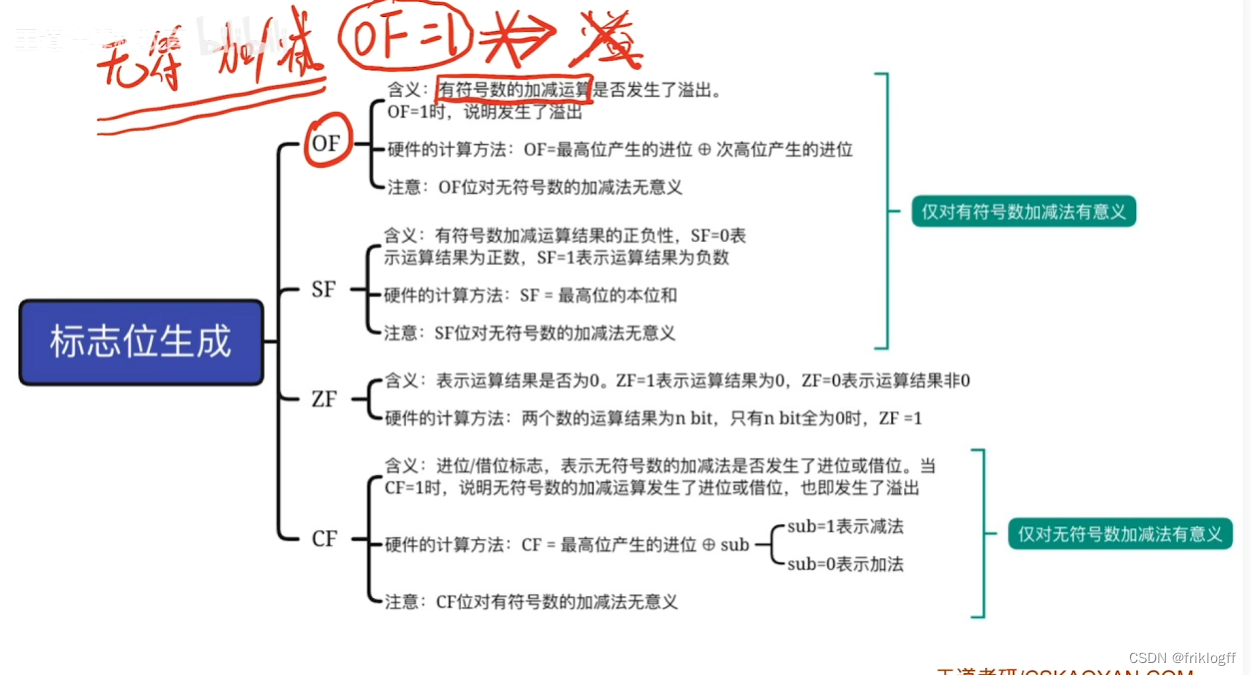
(OF)有符号数补码加减运算器溢出判断

(CF)无符号数补码加减运算器溢出判断

溢出判断

方法一
方法二

方法三

符号扩展

加减运算思维导图

加法器设计与实现

一位加法器（全加器）

• 输入：加数A和B，低位进位Cin

  • 输出：和：F = A ⊕ B ⊕ Cin
    高位进位：Cout=A·B + A·Cin + B·Cin

串行加法器

• n个全加器相连，进位触发器用来寄存进位信号，每一级进位依赖于前一级进位，进位信号逐级形成 Cout=A·B + (A⊕B)·Cin
  

并行加法器（单级/多级）

• 各级进位信号同时形成，又称先行进位，各进位之间无等待，相互独立并同时产生

  • 辅助函数：Gi = Ai·Bi Pi = Ai + Bi
    全加逻辑方程：Si = Pi⊕Ci Ci+1 = Gi + Pi·Ci

  • C1 = G0 + P0·C0
    C2 = G1 + P1·C1 = G1 + P1·G0 + P1·P0·C0
    C3 = G2 + P2·C2 = G2 + P2·G1 + P2·P1·G0 + P2·P1·P0·C0
    由上式可知：各进位之间无等待，相互独立并同时产生
    
    优化
    

n位带标志加法器

• 溢出标志OF（仅有符号数加减法有意义）
  • 含义：有符号数的加减法是否发生了溢出
  • 计算：OF=最高位产生的进位⊕次高位产生的进位
• 符号标志SF（仅有符号数加减法有意义）
  • 含义：有符号数加减运算结果的正负性
  • SF=最高位的本位和
• 零标志ZF
  • 含义：运算结果是否为0
  • 计算：n 位全0，ZF=1
• 进/借位标志CF（仅无符号加减法有意义）
  • 含义：加法时为进位标志，减法时为借位标志
  • 计算：CF=最高位进位⊕sub（减法sub=1，加法sub=0）

算数逻辑单元（ALU）

• 利用二路选择器+带标志加法器构造加/减运算器
• 加/减运算器基础上加寄存器、移位器、控制逻辑可实现ALU
  - 算数运算：取负、移位、加减乘除、扩展
  - 逻辑运算：与或非

这里74181中

• B3～B0和A3～A0是两个操作数，

• F3～F0为输出结果。

• C-l表示最低位的外来进位，

• Cn+4是7418l向高位的进位；

• P、G可供先行进位使用。

• M用于区别算术运算还是逻辑运算；

• S3～S0的不同取值可实现不同的运算。

• 输入B3～B0和A3～A0两个机器字长为4bit的信息

• 输出F3～F0机器字长为4bit的计算结果

• F3～F0存入寄存器X，寄存器的位数要与机器字长保持一致，所以寄存器的位数=机器字长

• S3～S0有4bit的信息，对应2^4=16种算数运算和逻辑运算
  知识回顾
  

C语言中各类运算

• 算术运算：无符号数、带符号的、浮点数的加减乘除运算

• 位运算：与、或、取反、异或

• 逻辑运算：&&、||、！

• 移位运算（王道分原码补码反码讨论，此处是C语言）

  • 逻辑左/右移（无符号数）

    • 高（低）位移出，低（高）位补0（若高位移出1，则左移发生溢出）

  • 算数左/右移（带符号数）

    • 左移：高位移出，低位补0（若移出位不等于新的符号位，则溢出）

    • 右移：低位移出，高位补符（可能数据丢失）

  • 循环移位

    • 带进位标志位的循环移位

    • 不带进位标志位的循环移位，移出的位需要同时进入进位寄存器

• 位扩展和位截断

  • 扩展

    • 无符号数：0扩展（前面补0）

    • 带符号数：符号扩展（前面补符）

  • 截断

    • 强行将高位丢弃，故可能发生溢出

定点数的运算

定点数的加减运算

可通过二路选择器+带标志加法器实现加/减运算器

• 计算机中所有运算都基于加法器实现

• 加法器不知道所运算的是带符号数还是无符号数

• 加法器不判定对错，总是取低n位为结果，并生成标志信息

• 无符号加法溢出条件：CF=1

  • 有符号加溢出条件：OF=1

• 无符号减法溢出：差为负数，即借位CF=1

  • 其他溢出判定方法见下方

• 减法做比较大小

  • 无符号数大于：CF=0

  • 有符号数大于：OF=SF

原码定点数加减法运算（符号不参与运算）

• 加法准则

  • 符号相同：绝对值相加，符号不变

  • 符号不同：绝对值大的减去绝对值小的，符号取绝对值大的

• 减法准则

  • 减数符号取反，做原码加法运算

补码定点数加减法运算（符号参与运算）

• 公式：[A+B]补=[A]补 + [B]补（MOD 2^n） [A-B]补=[A]补 + [-B]补（MOD 2^n）

补码溢出的判定方法

• 一位符号位

  • 参与运算的两个数符号相同，结果符号变化，则溢出

  • 最高位进位与次高位进位不同，则溢出

• 双符号位（存储仅一符号位，进入ALU后两位符号位）

  • 在乘除等运算中，为了不丢弃中间的溢出结果，多位符号位可以保留符号位和溢出的数值位，保留正确的中间结果

  • 00正数，无溢出

  • 01正溢出（符号位不同，最高位为真正符号）

  • 10负溢出（符号位不同，最高位为真正符号）

  • 11负数，无溢出

定点数的乘除运算

整数的乘运算

• 高级语言中两个n位整数相乘得到的结果也是n位整数，即取2n位乘积中的低n位

• 溢出问题（硬件不判溢出，仅保留2n位乘积）：乘积的高n位全0或全1，并等于低n位的最高位时不溢出（无符号高n位全0）

• 相同机器数无符号数和有符号数高n位可能不同，低n位相同，故指令分无符号数乘指令、有符号数乘指令

• 乘法运算比移位和加法等运算所用时间长，故往往用组合运算代替，例如x×20，20=2⁴⁺²2，故x×20=(x<<4)+(x<<2)

• 乘法实现细节可在考前看重新看一遍王道回忆细节，前期理解即可

整数的除法运算

• 整数除运算除了-2^(n-1)/-1会溢出，其他情况不溢出

• 不能整除时需要舍入

  • 正数：商取比自身小的最接近的整数

  • 负数：商取比自身大的最接近整数（加偏移量2^k-1，右移k位）

• 整数除法运算复杂，约30或更多时钟周期（除数为2的幂次形式，用右移代替）

• 除法实现细节可在考前看重新看一遍王道回忆细节，前期理解即可

浮点数的加减运算

• 对阶

  • 小阶看齐大阶，将阶码小的尾数右移一位，阶加一，直到两个数的阶码相等

• 尾数求和

• 规格化（若补码负数则关注第一个0位置，虽然IEEE754标准尾数是原码）

  • 最后形式：+/-1.xxx…xxx

  • 左规：结果为+/-0.0…01xxx…xxx时，需要左规，尾数左移一次，阶码减1，直到第一个1移到小数点左边，作为隐藏位

    • 每次阶码减1判断是否下溢，阶码下溢，结果为0

  • 右规：结果为+/-1x.xxx…xxx时，需要右规，尾数右移一次，阶码加1，直到第一个1移到小数点左边，作为隐藏位

    • 每次阶码加一后判断是否上溢，阶码上溢，中断处理

• 舍入

  • IEEE754舍入方式

    • 就近舍入（舍入为最近可表示的数）

      • 非中间数：0舍1入，中间数：强迫结果为偶数

    • 朝+∞方向舍入（+∞方向最近的可表示的数）

    • 朝-∞方向舍入（-∞方向最近的可表示的数）

    • 朝0方向舍入=直接截去

  • 舍入结果可能导致尾数未规格化，需再次右规判断溢出情况

• 若运算结果尾数为0，阶码也置0

例1


例2

不同类型转换

• char—>int

  • 前面补0

• int<—>unsigned

  • 都可能溢出丢失数据

• int—>float

  • 不会发生溢出，但可能有数据舍入

• double—>float或int

  • 可能发生溢出，可能舍入

• float或double—>int

  • 数据向0方向截断

• char—>int—>long—>double
  float—>double

  • 范围精度由小变大，无损失

浮点数的运算思维导图

考研真题

408 - 2023

下面是题目13的格式化表述：

13. 计算short型变量的机器数

若short型变量x=-8190，则x的机器数为【 】。

A. E002H

B. E001H

C. 9FFFH

D. 9FFEH

基础知识

在解析这个问题之前，让我们了解以下基础知识：

1. short型变量：short是一种整数数据类型，通常占用16位内存空间。在计算机内部，整数通常以补码形式表示。这意味着正数和负数都有相应的二进制表示。

2. 补码表示：补码是一种用于表示带符号整数的方法。正数的补码和原码相同，而负数的补码是将其绝对值的二进制表示按位取反，然后加1。

解析：
short型变量是补码表示的16位带符号整数。x是负数，可先求出8190的机器数，8190=8192-2=213- 2’,8190的机器数为0010 0000 0000 0000B -0000 0000 0000 0010B=0001 1111 11111110B，因此-8190的机器数为1110 0000 0000 0010B = E002H（按位取反，末位加1)。

首先，我们知道short型变量是16位的，因此需要计算-8190的16位补码表示。
2^13表示为10 0000 0000 0000(2)

1. 首先，计算8190的二进制表示：8190 = 2^13 - 2 = 1 1111 1111 1110。

2. 接下来，求-8190的补码，即将8190的二进制表示按位取反，然后加1。

   • 按位取反：
     • 0001 1111 1111 1110B
     • 1110 0000 0000 0001B
   • 加1：
     • 1110 0000 0000 0001B
     • +1↓
     • 1110 0000 0000 0010B

首先，将二进制数 1110 0000 0000 0010 分成四组，每组四个二进制位：

• 1110（二进制）对应于 E（十六进制）。
• 0000（二进制）对应于 0（十六进制）。
• 0000（二进制）对应于 0（十六进制）。
• 0010（二进制）对应于 2（十六进制）。

所以，x的机器数为1110 0000 0000 0010B。在十六进制表示中，答案是选项A：E002H。

14. 计算IEEE 754 单精度浮点数的值

已知float型变量用IEEE 754单精度浮点数格式表示。若float型变量x的机器数为80200000H，则x的值是什么？

A. -2^-128

B. -1.01x2^-127

C. -1.01x2^-126

D. 非数(NAN)
答案：A

基础知识

在解析这个问题之前，让我们了解以下基础知识：

• IEEE 754 单精度浮点数：IEEE 754是一种标准，用于表示浮点数在计算机中的二进制格式。单精度浮点数使用32位二进制格式，分为符号位、阶码和尾数。

• 规格化数（normalized numbers）：对于规格化数，阶码部分不全为0或全为1，而是以一定的方式表示浮点数的阶。这使得浮点数可以表示较大或较小的数值范围。

• 非规格化数（denormalized numbers）：当阶码部分全为0时，就进入了非规格化数的领域。在这种情况下，尾数部分不再表示1.xxxx的形式，而是0.xxxx的形式。这意味着非规格化数表示非常接近零的小数值，但失去了一些精度。

16. 溢出和借位标志问题

问题： 已知 x 和 y 为 int 类型，当 x=100, y=200 时，执行“x减y”指令的到的溢出标志 OF 和借位标志 CF 分别为 0, 1，那么当 x=10, y=-20 时，执行该指令得到的 OF 和 CF 分别是（ ）。

A. OF=0, CF=0

B. OF=0, CF=1

C. OF=1, CF=0

D. OF=1, CF=1

答案：B. OF=0, CF=1

基础知识：

int为32位有符号整型，int 为 32 位有符号短整型，用补码表示，最高位为符号位，
表示范围为

当 x=10, y=-20 时，x-y=30，显然在表示范围之内，不溢出，OF=0。

当 x=10, y=-20 时，[x]补=[x]原=0000 0000 0000 0000 0000 0000 0000 1010B=0000000AH，[y]原=1000 0000 0000 0000 0000 0000 0001 0100B，[y]补=1111 1111 1111 1111 1111 1111 1110 1100=FFFFFFECH，显然0000000AH-FFFFFFECH不够减，需要借位，CF=1。

408 - 2022

13. 32位补码整数范围

问题： 32位补码所能表示的整数范围是？

A. -2^32 到 2^31 - 1

B. -2^31 到 2^31 - 1

C. -2^22 到 2^32 - 1

D. -2^31 到 2^32 - 1

答案： B. -2^31 到 2^31 - 1

基础知识： 在32位补码表示中，最高的1位用于表示符号位（0表示正数，1表示负数），剩下的31位用于表示数值。因此，32位补码可以表示的整数范围是从-2^31到231-1。

当然，以下是按照之前的结构以Markdown形式重构的题目和答案：

14. IEEE754单精度浮点数表示

问题： -0.4375的IEEE754单精度浮点数表示为何？

A. BEE0 0000H

B. BF60 0000H

C. BF70 0000H

D. C0E0 0000H

答案： A. BEE0 0000H

基础知识：

-0.4375=-1.75×2^-2，符号S =1，阶码E=-2＋127= 125= 01111101B，尾数0.75=0.11B，
补齐至23位M = 110 0000 0000 0000 0000 0000B。

IEEE754单精度浮点数的格式包括符号位、阶码和尾数部分，总共32位。-0.4375的IEEE 754单精度浮点表示如下：

• 符号位：0（表示正数）
• 阶码部分：01111101（对应的十进制为125）
• 尾数部分：110 0000 0000 0000 0000 0000

拼接起来为BEE0 0000H。

408 - 2021

13. 带符号整数的补码表示与大小比较

问题： 已知带符号整数用补码表示，变量 x，y，z 的机器数分别为 FFFDH，FFFDFH，7FFCH，下列结论中，正确的是？

A. 若 x、y 和 z 为无符号整数，则 z < x < y

B. 若 x、y 和 z 为无符号整数，则 x < y < z

C. 若 x、y 和 z 为带符号整数，则 x < y < z

D. 若 x、y 和 z 为带符号整数，则 y < x < z

答案：D

基础知识：

1. 带符号整数的补码表示：在计算机中，带符号整数通常使用补码表示。在补码中，最高位为符号位（0 表示正数，1 表示负数），其余位表示数值。

2. 大小比较规则：对于带符号整数的补码表示，如果两个数的符号位不同，那么符号位为 0 的数更大；如果两个数的符号位相同，那么数值部分越大的数更大。

根据题目中给出的机器数：

• x 的机器数 FFFDH 表示的是负数，其原码为 1000 0000 0000 0010B，转换成十进制为 -3。
• y 的机器数 FFFFH 表示的是负数，其原码为 1000 0000 0000 0001B，转换成十进制为 -1。
• z 的机器数 7FFCH 表示的是正数，其原码为 0111 1111 1111 1100B，转换成十进制为 2044。

根据大小比较规则，有 -3 < -1 < 2044，因此 y < x < z。

所以正确答案是 D. 若 x、y 和 z 为带符号整数，则 y < x < z。

14. IEEE754浮点格式表示精度问题

问题： 下列数值中，不能用 IEEE754 浮点格式精确表示的是？

A. 1.2

B. 1.25

C. 2.0

D. 2.5

答案：A

基础知识：

IEEE754 是一种用于表示浮点数的标准格式，它使用科学计数法来表示浮点数，包括三个部分：符号位、指数部分和尾数部分。IEEE754 浮点格式的小数部分通常采用二进制表示。

在 IEEE754 浮点格式中，有效数字部分通常表示成规格化的形式，即一个小数乘以 2 的幂次方。有效数字的小数部分通常是 1 和 0 组成的二进制小数。

对于一个数值能够被精确表示为 IEEE754 浮点数，其小数部分必须满足以下条件：

• 可以表示成 (1 + 1/2 + 1/4 + 1/8 + …) 的形式，其中分母是 2 的幂次方。

现在来分析选项中的数值：

A. 1.2 = 6/5 = 1 + 1/5，不满足上述条件，因此不能用 IEEE754 浮点格式精确表示。

B. 1.25 = 5/4 = 1 + 1/4，满足上述条件，可以用 IEEE754 浮点格式精确表示。

C. 2.0 = 2，可以表示成 2 的幂次方，满足条件，可以用 IEEE754 浮点格式精确表示。

D. 2.5 = 5/2 = 1 + 1/2，满足上述条件，可以用 IEEE754 浮点格式精确表示。

所以，不能用 IEEE754 浮点格式精确表示的是 A. 1.2。

（未完待续，逐张试卷分析中）