• 【重拾C语言】六、批量数据组织（一）数组（数组类型、声明与操作、多维数组；典例：杨辉三角、矩阵乘积、消去法）

    目录

    前言

    六、批量数据组织——数组

    6.1 成绩统计——数组类型

    6.1.1 数组类型

    6.1.2 数组声明与操作

    6.1.3 成绩统计

    6.2 统计多科成绩——多维数组

    6.3 程序设计实例

    6.3.1 杨辉三角形

    6.3.2 矩阵乘积

    6.3.3 消去法

    6.4 线性表——分类与检索

    前言

    ChatGPT

            C语言是一种通用的、过程式的计算机编程语言，由贝尔实验室的Dennis Ritchie在20世纪70年代初开发。它被设计成一种简单、高效和可移植的语言，用于系统级编程和应用程序开发。

    以下是C语言的一些主要特点：

    1. 结构化编程：C语言支持结构化编程，它提供了顺序执行、条件语句（如if-else和switch）和循环结构（如for和while），使程序更易于阅读、理解和维护。

    2. 中级语言：C语言同时具备高级语言和低级语言的特点。它提供了丰富的控制结构和操作符，可以直接访问内存和硬件，并且允许程序员进行底层的操作，如位操作和指针运算。

    3. 可移植性：C语言编写的程序具有很高的可移植性，因为它的语法和特性在不同的计算机系统上基本保持一致。这使得程序可以在不同的平台上进行编译和执行，而无需对代码进行太多的修改。

    4. 强大的标准库：C语言提供了一个丰富的标准库，其中包含了各种函数和工具，用于处理输入输出、字符串操作、内存管理、数学运算等。这些函数可以提高程序开发的效率，并且可以跨平台使用。

    5. 面向系统编程：由于C语言具有直接访问内存和硬件的能力，它经常用于开发操作系统、嵌入式系统和驱动程序等底层软件。C语言还提供了位操作和指针等特性，使得程序员可以更好地控制系统资源。

    6. 扩展性：C语言允许程序员编写自定义的函数和库，以扩展语言的功能。这使得C语言非常适合大型项目的开发，可以将代码组织成模块化的结构，并通过函数调用进行复用。

            尽管C语言相对较为底层，但它仍然是一种非常重要和广泛应用的编程语言。它为程序员提供了强大的控制能力和性能优势，并且在各种领域，如系统编程、嵌入式开发、游戏开发等方面都得到了广泛应用。许多现代编程语言，如C++、Java和Python，都受到了C语言的影响，并在其基础上进行了扩展和改进。

            C语言中的数组是一种用于存储多个相同类型元素的数据结构。它是一种线性数据结构，可以按照索引访问和操作其中的元素。数组在C语言中被广泛应用于各种编程任务，包括数据的组织、存储和处理。同时，数组也是其他数据结构和算法的基础，如字符串、栈、队列、排序算法等。

    六、批量数据组织——数组

    6.1 成绩统计——数组类型

    6.1.1 数组类型

    • 数组是个数固定、类型相同的若干个变量的有序集合；
    • 数组中的变量称为数组元素；
    • 通常用数组来表示向量、矩阵等；
    • 举例： 
      • int a[50],j[11] ;

      • 一个单词 由  若干个    字符   组成 
        • char word[1000];

      • 一个向量 由  若干个    实数  组成 
        • float data[4];

      • 一个矩阵 由  若干个    向量  组成 
        • float vector[2][4];

    6.1.2 数组声明与操作

            在C语言中，声明一个数组需要指定元素的类型和数组的名称，还可以指定数组的大小（即元素的数量）。以下是一个示例的数组声明：    

            79b28db9022d452487302e2a2e947185.png

            在上述示例中，我们声明了一个名为a的整型数组，它包含了5个元素。

            数组的元素可以通过索引访问，索引从0开始，依次增加。例如，要访问数组中的第一个元素，可以使用numbers[0]；要访问第三个元素，可以使用numbers[2]。我们可以使用索引来读取、修改或赋值数组中的元素。  

            注意：数组的有效索引范围是从0到数组大小减1。如果尝试访问超出数组边界的索引，将导致未定义的行为或错误。

    6.1.3 成绩统计

    1. #include 
    2.  
    3. #define SIZE 5
    4.  
    5. int main() {
    6.     int scores[SIZE]; // 存储成绩的数组
    7.     int i;
    8.     int sum = 0;
    9.     float average;
    10.  
    11.     // 读取成绩
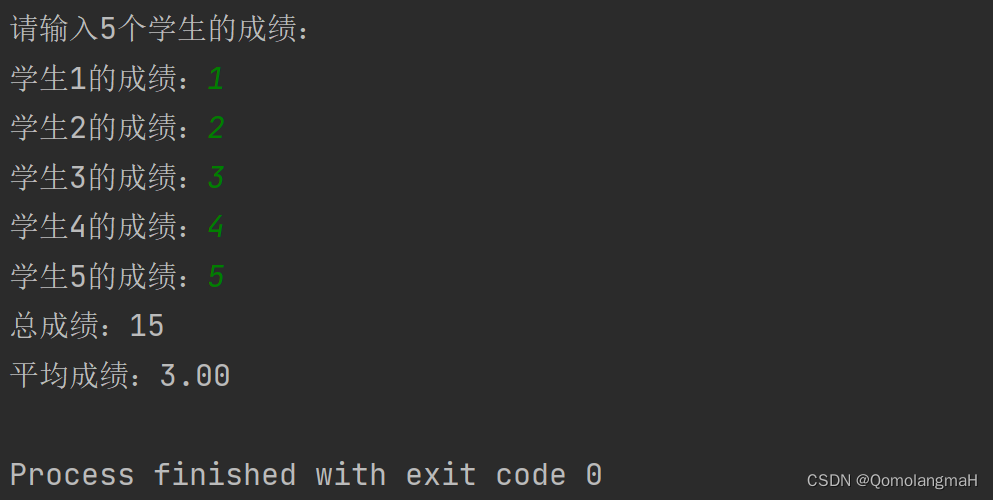
    12.     printf("请输入%d个学生的成绩：\n", SIZE);
    13.     for (i = 0; i < SIZE; i++) {
    14.         printf("学生%d的成绩：", i + 1);
    15.         scanf("%d", &scores[i]);
    16.     }
    17.  
    18.     // 计算总分
    19.     for (i = 0; i < SIZE; i++) {
    20.         sum += scores[i];
    21.     }
    22.  
    23.     // 计算平均成绩
    24.     average = (float)sum / SIZE;
    25.  
    26.     // 打印结果
    27.     printf("总成绩：%d\n", sum);
    28.     printf("平均成绩：%.2f\n", average);
    29.  
    30.     return 0;
    31. }

    8238405bbd42421e9e1f2d4cacf9ae8c.png

    6.2 统计多科成绩——多维数组

           C语言的数组还支持多维数组的概念。多维数组是指包含多个维度的数组，可以用于表示表格、矩阵等复杂的数据结构。例如，以下是一个二维数组的声明和访问示例：

    1. int matrix[3][3]; // 声明一个3x3的整型矩阵
    2.  
    3. // 访问矩阵中的元素
    4. matrix[0][0] = 1; // 第一行第一列的元素
    5. matrix[1][2] = 5; // 第二行第三列的元素

            在上述示例中，声明了一个名为matrix的二维整型数组，它是一个3x3的矩阵。通过使用两个索引，我们可以访问矩阵中的特定元素。

    1. #include 
    2.  
    3. #define NUM_STUDENTS 5
    4. #define NUM_SUBJECTS 3
    5.  
    6. int main() {
    7.     int scores[NUM_STUDENTS][NUM_SUBJECTS]; // 存储成绩的二维数组
    8.     int i, j;
    9.     int sum[NUM_STUDENTS] = {0}; // 每个学生的总分
    10.     float average[NUM_STUDENTS]; // 每个学生的平均成绩
    11.  
    12.     // 读取成绩
    13.     printf("请输入%d个学生的%d门成绩：\n", NUM_STUDENTS, NUM_SUBJECTS);
    14.     for (i = 0; i < NUM_STUDENTS; i++) {
    15.         printf("学生%d的成绩：\n", i + 1);
    16.         for (j = 0; j < NUM_SUBJECTS; j++) {
    17.             printf("科目%d：", j + 1);
    18.             scanf("%d", &scores[i][j]);
    19.             sum[i] += scores[i][j];
    20.         }
    21.         average[i] = (float)sum[i] / NUM_SUBJECTS;
    22.     }
    23.  
    24.     // 打印结果
    25.     printf("\n学生成绩统计：\n");
    26.     for (i = 0; i < NUM_STUDENTS; i++) {
    27.         printf("学生%d的总成绩：%d\n", i + 1, sum[i]);
    28.         printf("学生%d的平均成绩：%.2f\n\n", i + 1, average[i]);
    29.     }
    30.  
    31.     return 0;
    32. }

    1. 请输入5个学生的3门成绩：
    2. 学生1的成绩：
    3. 科目1：1
    4. 科目2：2
    5. 科目3：3
    6. 学生2的成绩：
    7. 科目1：4
    8. 科目2：5
    9. 科目3：6
    10. 学生3的成绩：
    11. 科目1：7
    12. 科目2：8
    13. 科目3：9
    14. 学生4的成绩：
    15. 科目1：9
    16. 科目2：8
    17. 科目3：7
    18. 学生5的成绩：
    19. 科目1：6
    20. 科目2：5
    21. 科目3：4
    22.  
    23. 学生成绩统计：
    24. 学生1的总成绩：6
    25. 学生1的平均成绩：2.00
    26.  
    27. 学生2的总成绩：15
    28. 学生2的平均成绩：5.00
    29.  
    30. 学生3的总成绩：24
    31. 学生3的平均成绩：8.00
    32.  
    33. 学生4的总成绩：24
    34. 学生4的平均成绩：8.00
    35.  
    36. 学生5的总成绩：15
    37. 学生5的平均成绩：5.00

    6.3 程序设计实例

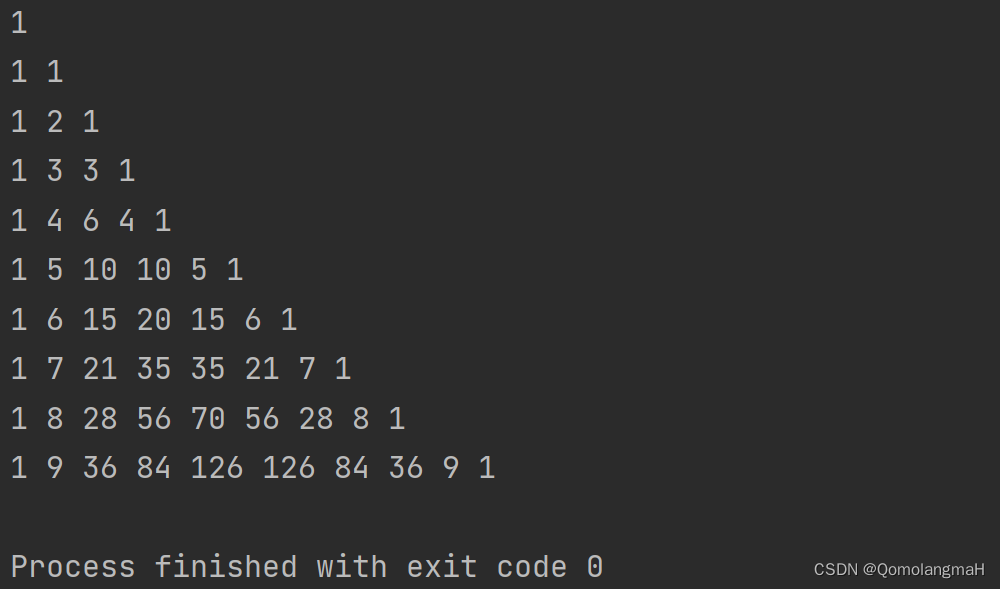
    6.3.1 杨辉三角形

            杨辉三角形是一个由数字排列成三角形的数列，它的每个数字等于它上方两个数字的和。以下是使用一维数组实现的杨辉三角形的打印代码示例：

    1. #include 
    2.  
    3. #define MAX_ROWS 10
    4.  
    5. int main() {
    6.     int triangle[MAX_ROWS][MAX_ROWS];
    7.     
    8.     // 初始化杨辉三角形的第一列和对角线为1
    9.     for (int i = 0; i < MAX_ROWS; i++) {
    10.         triangle[i][0] = 1;
    11.         triangle[i][i] = 1;
    12.     }
    13.     
    14.     // 计算并填充杨辉三角形的其他元素
    15.     for (int i = 2; i < MAX_ROWS; i++) {
    16.         for (int j = 1; j < i; j++) {
    17.             triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j];
    18.         }
    19.     }
    20.     
    21.     // 打印杨辉三角形
    22.     for (int i = 0; i < MAX_ROWS; i++) {
    23.         for (int j = 0; j <= i; j++) {
    24.             printf("%d ", triangle[i][j]);
    25.         }
    26.         printf("\n");
    27.     }
    28.     
    29.     return 0;
    30. }

    b063a3493aef4b68ae5571554722931f.png

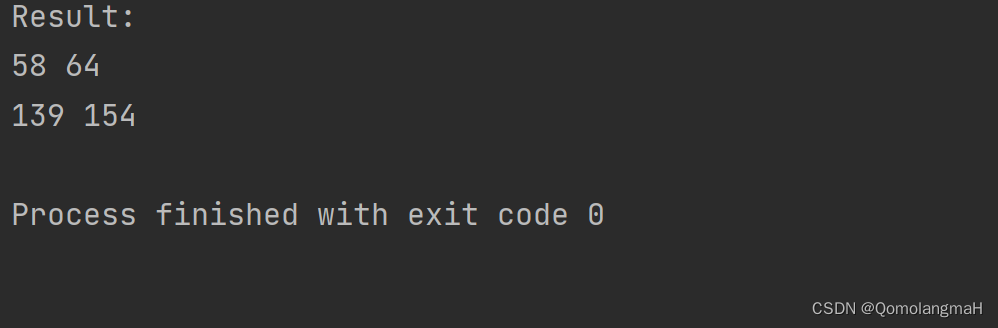
    6.3.2 矩阵乘积

            矩阵乘积是指两个矩阵相乘得到的结果矩阵。

    1. #include 
    2.  
    3.  
    4. #define ROWS_A 2
    5. #define COLS_A 3
    6. #define ROWS_B 3
    7. #define COLS_B 2
    8.  
    9. void matrixMultiply(int A[ROWS_A][COLS_A], int B[ROWS_B][COLS_B], int C[ROWS_A][COLS_B]) {
    10.     for (int i = 0; i < ROWS_A; i++) {
    11.         for (int j = 0; j < COLS_B; j++) {
    12.             C[i][j] = 0;
    13.             for (int k = 0; k < COLS_A; k++) {
    14.                 C[i][j] += A[i][k] * B[k][j];
    15.             }
    16.         }
    17.     }
    18. }
    19.  
    20. int main() {
    21.     int matrixA[ROWS_A][COLS_A] = {{1, 2, 3}, {4, 5, 6}};
    22.     int matrixB[ROWS_B][COLS_B] = {{7, 8}, {9, 10}, {11, 12}};
    23.     int result[ROWS_A][COLS_B];
    24.  
    25.     matrixMultiply(matrixA, matrixB, result);
    26.  
    27.     printf("Result:\n");
    28.     for (int i = 0; i < ROWS_A; i++) {
    29.         for (int j = 0; j < COLS_B; j++) {
    30.             printf("%d ", result[i][j]);
    31.         }
    32.         printf("\n");
    33.     }
    34.  
    35.     return 0;
    36. }

    e6ed604c03d04d84b66571093ddccbf1.png

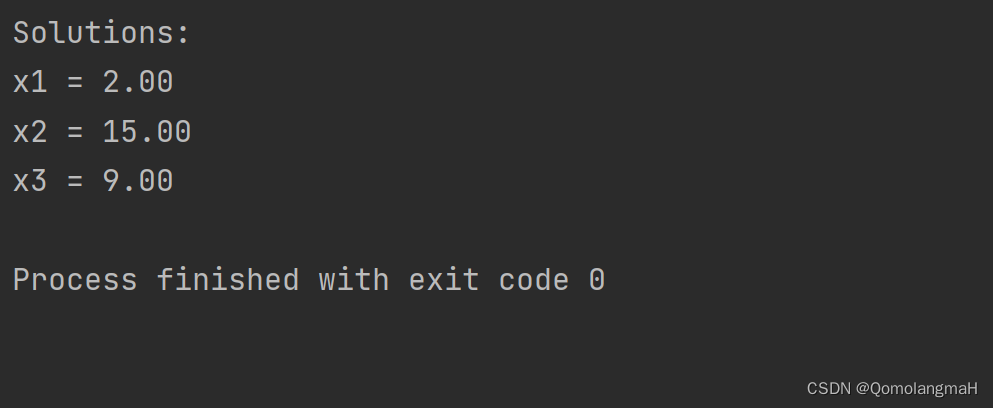
    6.3.3 消去法

            消去法是一种解线性方程组的方法，通过行变换将方程组化为上三角形矩阵，然后回代求解未知数。

    1. #include 
    2.  
    3. #define SIZE 3
    4.  
    5. void gaussianElimination(float matrix[SIZE][SIZE], float constants[SIZE], float solutions[SIZE]) {
    6.     for (int k = 0; k < SIZE - 1; k++) {
    7.         for (int i = k + 1; i < SIZE; i++) {
    8.             float factor = matrix[i][k] / matrix[k][k];
    9.             for (int j = k; j < SIZE; j++) {
    10.                 matrix[i][j] -= factor * matrix[k][j];
    11.             }
    12.             constants[i] -= factor * constants[k];
    13.         }
    14.     }
    15.     
    16.     for (int i = SIZE - 1; i >= 0; i--) {
    17.         solutions[i] = constants[i];
    18.         for (int j = i + 1; j < SIZE; j++) {
    19.             solutions[i] -= matrix[i][j] * solutions[j];
    20.         }
    21.         solutions[i] /= matrix[i][i];
    22.     }
    23. }
    24.  
    25. int main() {
    26.     float matrix[SIZE][SIZE] = {{2, -1, 1}, {-3, 2, -2}, {1, -1, 2}};
    27.     float constants[SIZE] = {-2, 6, 5};
    28.     float solutions[SIZE];
    29.     
    30.     gaussianElimination(matrix, constants, solutions);
    31.     
    32.     printf("Solutions:\n");
    33.     for (int i = 0; i < SIZE; i++) {
    34.         printf("x%d = %.2f\n", i+1, solutions[i]);
    35.     }
    36.     
    37.     return 0;
    38. }

    c2a3b4e2691a4d01a9625fed3dfeb16e.png

    6.4 线性表——分类与检索

    【重拾C语言】六、批量数据组织（二）线性表——分类与检索（主元排序、冒泡排序、插入排序、顺序检索、对半检索）_QomolangmaH的博客-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/m0_63834988/article/details/133620693?spm=1001.2014.3001.5501

  • 相关阅读:
    springboot+jsp+ssm助农系统农产品宣传网站设计
    K8s之Replicaset控制器详解
    PowerShell系列（十二）：PowerShell Cmdlet高级参数介绍（二）
    OpUtils局域网唤醒：远程引导计算机
    万丈高楼平地起——基于飞桨PaddleGAN与PaddleRS实现建筑物样本扩充工具
    Redis常用命令补充和持久化
    ImageMagick命令注入漏洞(CVE-2016–3714)
    C++类型转换
    就近值 reduce用法 时间戳与时间点对比循环查找
    基于springboot医院碳排放管理平台设计与实现-计算机毕业设计源码+LW文档
  • 原文地址：https://blog.csdn.net/m0_63834988/article/details/133580645