O（根号n/ln（根号n））时间复杂度内求n的所有因子

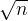O（）复杂度内求n的所有因子，在2e9数量级比O（）快10倍左右

先用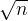范围内的质数除n，求出n的分解质因数形式，然后爆搜求出n的所有因子，

n范围内的质数大约有个，所以是这个时间复杂度。

2e9范围内因子最多的数有1600个因子，爆搜的时间复杂度很小

#include
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
 
const int N = 50010;
 
int primes[N], cnt;
bool st[N];
PII factor[N];
int fcnt;
int dive[N], dcnt;
 
void init()
{
	for(int i = 2; i < N; i ++)
	{
		if(!st[i])primes[cnt ++] = i;
		for(int j = 0; primes[j] * i < N; j ++)
		{
			st[primes[j] * i] = true;
			if(i % primes[j] == 0)break;
		}
	}
}
 
void dfs(int u, int num)
{	
	if(u == fcnt)
	{
		dive[dcnt ++] = num;
		return;
	}
	
	int p = factor[u].first, c = factor[u].second;
	for(int i = 0; i <= c; i ++)
	{
		dfs(u + 1, num);
		num *= p;
	}
}
 
int main()
{
	IOS
	init();
	
	int n;
	cin >> n;
	while(n --)
	{
		int a0, a1, b0, b1;
		cin >> a0 >> a1 >> b0 >> b1;
		fcnt = 0;
		
		int d = b1;
		for(int i = 0; primes[i] <= d / primes[i]; i ++)
		{
			int p = primes[i];
			if(d % p == 0)
			{
				int c = 0;
				while(d % p == 0)
				{
					d /= p;
					c ++;
				}
				factor[fcnt ++] = {p, c};
			}
		}
		if(d > 1)factor[fcnt ++] = {d, 1};
		
		dcnt = 0;
		dfs(0, 1);
		
		int ans = 0;
		for(int i = 0; i < dcnt; i ++)
		{
			int x = dive[i];
			if(__gcd(x, a0) == a1 && (ll)x * b0 / __gcd(x, b0) == b1)ans ++;
		}
		cout << ans << endl;
	}
	
	return 0;
} 

如果n范围小于1e8的话还可以用  log时间复杂度求质因子  的算法将求因数优化到log级别。