标准差椭圆算法实现

一、标准差椭圆介绍

（一）方法介绍        

        标准差椭圆是一种用于描述多元数据集的离散程度和相关性的可视化工具。它可以帮助我们直观地了解数据的分布情况、方向和离散程度，以及不同变量之间的关系。

        标准差椭圆的计算公式如下：

     

        椭圆的中心点是数据集的均值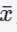，其方向由对应于特征值最大和次大的两个特征向量所定义。如果两个特征值相等，则椭圆沿着任何方向都可以。

        需要注意的是，标准差椭圆假设数据服从多元正态分布，并且假定数据集没有缺失值。在实际应用中，我们应该根据具体情况来判断是否适合使用标准差椭圆进行分析，并结合其他的统计方法和领域知识来进行综合判断。

（二）结果的粗略解读

        椭圆的大小：椭圆的半长轴和半短轴长度与数据的标准差相关。较大的椭圆表示数据具有较大的离散程度，而较小的椭圆表示数据相对集中。

        椭圆的形状：椭圆的形状可以反映数据的相关性。如果椭圆比较接近一个圆形，则表示数据之间的相关性相对较低。如果椭圆呈现出拉长的形状，则表示数据之间存在较强的线性相关性。

        椭圆的方向：椭圆的方向表示数据集的主要方向。主要方向与特征向量相关，它们指示了数据集中变化最大的方向。如果椭圆的方向与坐标轴平行，则表示数据集在相应的特征值方向上具有更大的变化。

二、实现标准差椭圆的方法

       （一）python实现标准差椭圆的代码

        示例代码中定义了一个名为plot_std_ellipse的函数，用于计算并绘制标准差椭圆。该函数接收一个二维数据数组data作为输入，并可选地指定透明度alpha（默认为0.5）。函数内部首先计算数据的均值和协方差矩阵，然后通过计算特征值和特征向量得到椭圆的参数。接下来，根据参数生成椭圆的点坐标，并使用Matplotlib库绘制散点图和椭圆。最后，调用示例数据并调用plot_std_ellipse函数进行绘图。

import numpy as np
import matplotlib.pyplot as plt
 
def plot_std_ellipse(data, alpha=0.5):
    # 计算均值和协方差矩阵
    mean = np.mean(data, axis=0)
    cov = np.cov(data, rowvar=False)
 
    # 计算特征值和特征向量
    eigenvalues, eigenvectors = np.linalg.eig(cov)
 
    # 计算标准差椭圆的半长轴和半短轴
    std_dev_1 = np.sqrt(eigenvalues[0]) * 2
    std_dev_2 = np.sqrt(eigenvalues[1]) * 2
 
    # 计算椭圆在标准差内的角度
    angle = np.arctan2(eigenvectors[1, 0], eigenvectors[0, 0])
 
    # 生成椭圆的点坐标
    t = np.linspace(0, 2*np.pi, 100)
    ellipse_x = mean[0] + std_dev_1 * np.cos(t) * np.cos(angle) - std_dev_2 * np.sin(t) * np.sin(angle)
    ellipse_y = mean[1] + std_dev_1 * np.cos(t) * np.sin(angle) + std_dev_2 * np.sin(t) * np.cos(angle)
 
    # 绘制散点图和椭圆
    plt.scatter(data[:, 0], data[:, 1])
    plt.plot(ellipse_x, ellipse_y, color='red', alpha=alpha)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.title('Standard Deviation Ellipse Analysis')
    plt.axis('equal')
    plt.show()
 
# 示例数据
data = np.random.multivariate_normal([0, 0], [[2, 1], [1, 2]], 100)
 
# 绘制标准差椭圆
plot_std_ellipse(data)

（二）Arc Map实现标标准差椭圆分析

        案例描述：现有江西省 11个地级市市的矢量地图以及相应年份人均 GDP 属性数据，通过空间自相关分析江西省人均GDP空间分布方向性变化。对应操作视频见引用3（视频不对应但包含其中）。
        1、加载江西省市域图层，并与相关年份人均 ＧＤＰ 属性数据进行连接 操作。
        2、打开工具箱→【空间统计工具】→【度量地理分布】→【方向分布标准差椭圆】
        3、弹出对话框，按照下图进行参数设置，【输入要素类】项输入江西省地 级市图层，【椭圆大小】通常选一个标准差，【权重字段】里输入所要研究的经济 属性字段，这里输入 2011年人均 GDP。完成参数设置后，点击确定。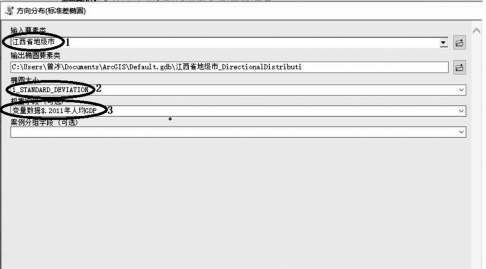

        4、工具计算完毕后，返回 GIS窗口，即可看到标准差椭圆图层，如图: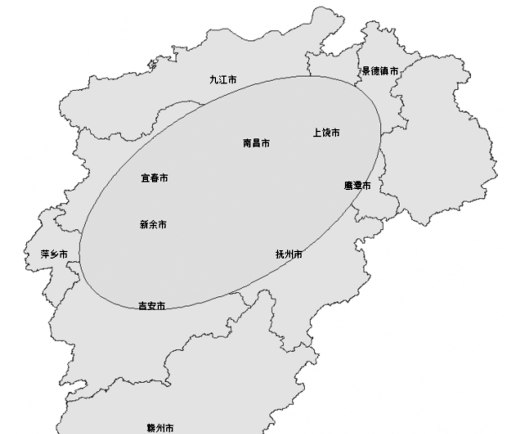

        5、由于椭圆图层覆盖在江西省地级市图层上，导致原图层难以有效标 识，南昌、宜春等地市的边界被覆盖掉，故需通过符号选择器对椭圆图层符号进 行修改，将其设置为空心，提高轮廓宽度，从而有效地显示两类图层。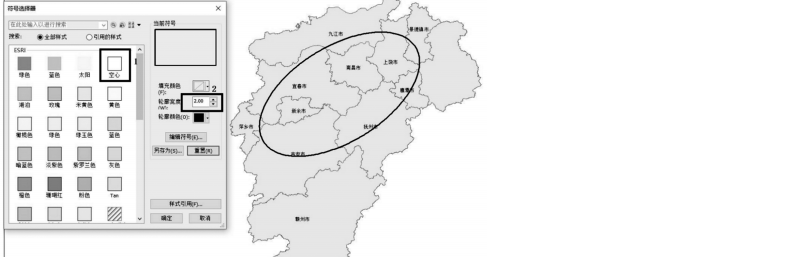

        6、打开椭圆图层属性表，可以看到 Shape-leng\ Shape-Aera \Center X\ Center Y\X Std Dist\Y Std Dist \Rotation 等字段。

        7、按照上述操作，对 2016 年人均 GDP进行标准差椭圆分析，并于 2011年进行对比分析。下图 中颜色更深黑色圈代表 2011 年，颜色更浅代表 2016年。

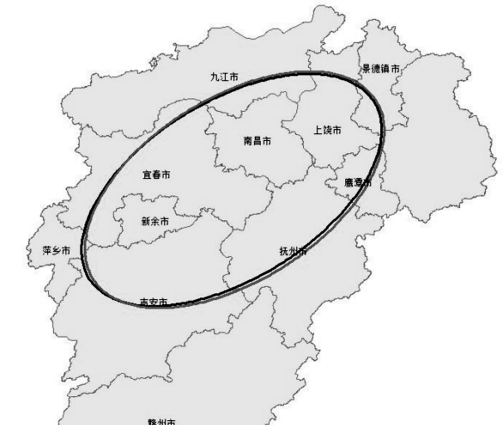
        8将 2011年与 2016 年图层属性表内容导出，对相关字段内容加以对比。 需要注意的是，由于在处理图层时未进行投影坐标系转化，故椭圆长度、面积表 示的是弧度单位。

        从生成面积表示范围，可以发现 2016年 的经济发展范围要大于 2011 年；扁 率表示他的方向明确性和向心力的程度，2016年生成的椭圆扁率低于 2011 年 的，说明了 2016的经济发展情况比 2011 年的方向趋势更明显。空间旋转角变化来看，旋转角由 2011 年的 58.263°降低到2016 年的57.675°，生成的椭圆方向与鄱阳湖生态经济区发展方向基本相符，所以鄱阳湖生态经济区在江西经济发展扮演着重要角色。
        此外，江西经济发展空间分布格局的重心移动路 径总体呈现向东北方向移动的趋势，由 2011 年的（115.712、28.149）移动到 2016 年的（115.744、28.152）。原因在于：受昌九一体化、鄱阳湖生态经济区、 长江中游城市群等战略的影响，资本、技术、固定资产投资及外商投资等向江西北部、东部地区转移。长半轴由 2011 年的 1.747 降至 2016 年的 1.744，下降幅度都较小，表明经济发展空间分布在主要方向上越来越集聚，但是集聚的 幅度不大，短半轴则由 0.925 上升至 0.953，椭圆长轴缩短、短轴增长，说明该阶段江西省经济发展空间分布格局较为稳定，经济发展空间溢出效应尚不明显，空间分布格局仍以南 -北方向为主导，东- 西方向的影响较弱。

三、结果解读

（一）常规结果数据分析  

      (1)椭圆的长半轴表示的是数据分布的方向，短半轴表示的是数据分布的范围，长短半轴的值差距越大（扁率越大），表示数据的方向性越明显。反之，如果长短半轴越接近，表示方向性越不明显。如果长短半轴完全相等，就等于是一个圆了，圆的话就表示没有任何的方向特征。

        (2)短半轴表示数据分布的范围，短半轴越短，表示数据呈现的向心力越明显；反之，短半轴越长，表示数据的离散程度越大。同样，如果短半轴与长半轴完全相等了，就表示数据没有任何的分布特征。

        (3)中心点表示了整个数据的中心位置，一般来说，只要数据的变异程度不是很大的话，这个中心点的位置大约与算数平均数的位置基本上是一致的，至于数据变异是什么情况，请看下面第4点。

        (4)关于标准差椭圆分析的补充介绍

        “标准差椭圆”在Arc MAP中会生成三个级别的椭圆，分别表示了你生成的椭圆，能够包含68%，95%和99%三个级别的数据，当要素具有空间正态分布时（即这些要素在中心处最为密集，而在接近外围时会逐渐变得稀疏），第一级标准差（默认值）范围可将约占总数 68% 的输入要素的质心包含在内。第二级标准差范围会将约占总数 95% 的要素包含在内，而第三级标准差范围则会覆盖约占总数 99% 的要素的质心。

（5）其余常识

        点的疏密：包含点数据的分布探索，是否一致、均匀或者不均匀。点的方位：包含点的分布和方向。点的数量：多少（极值和均值）。点的大小：代表的含义（如点一个点代表多少人口）。

（二） Arc Map结果数据分析

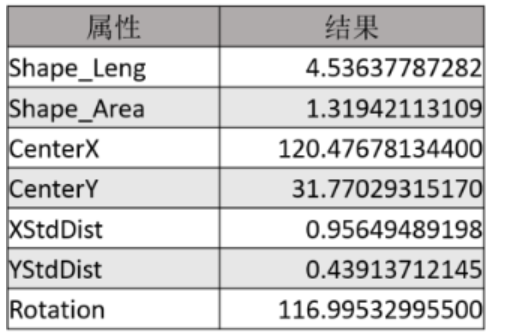
        当中，Shape_Leng和Shape_Area是生成的椭圆的周长和面积。单位与你数据的单位同样，这里我的数据是经纬度的，所以生成的结果仅仅能作为相对參考结果。CenterX和CenterY表示的是椭圆的中心点。XstdDist和YStdDist表示的X轴的长度和Y轴的长度。Rotation表示的是椭圆的方向角度。

四、参考引用

[1]新版白话空间统计（25）：方向分布（标准差椭圆） - 知乎 (zhihu.com)

[2]Arcgis空间分布方向性分析_标准差椭圆-CSDN博客

[3]基于GIS的标准差椭圆及重心迁移制作上：标准差椭圆