十天学完基础数据结构-第七天（图（Graph））

图的基本概念

图是一种数据结构，用于表示对象之间的关系。它由两个基本组件构成：

• 顶点（Vertex）：也被称为节点，代表图中的对象或实体。

• 边（Edge）：连接两个顶点的线，表示顶点之间的关系。

有向图和无向图的区别

图可以分为两种主要类型：

• 无向图（Undirected Graph）：边没有方向，表示两个顶点之间的关系是双向的。想象你和朋友之间的社交网络关系图，这就是一个无向图的例子。

• 有向图（Directed Graph）：边有方向，表示从一个顶点到另一个顶点的关系是单向的。一个典型的有向图示例是网页链接图，其中箭头表示链接方向。

图的遍历方法

遍历图意味着访问图中的所有顶点和边。两种常见的图遍历方法如下：

• 深度优先搜索（DFS）：DFS从起始顶点开始，沿着一条路径尽可能深入，直到无法继续为止，然后回溯到其他路径。这种方法类似于探险，一直往前走直到没有未探索的路径。

• 广度优先搜索（BFS）：BFS从起始顶点开始，首先访问所有直接相邻的顶点，然后逐层向外扩展。这种方法类似于水波扩散，先探索离起点最近的区域，然后逐渐扩展到更远的区域。

任务

创建和操作图数据结构，以及理解图的遍历算法。

示例代码 - 使用C++创建简单的无向图：

#include 
#include 

class Graph {
public:
    Graph(int vertices) : V(vertices) {
        adj = std::vector<std::vector<int>>(vertices);
    }

    void addEdge(int v, int w) {
        adj[v].push_back(w);
        adj[w].push_back(v);
    }

    void printGraph() {
        for (int v = 0; v < V; ++v) {
            std::cout << "顶点 " << v << " 的邻居: ";
            for (const int& neighbor : adj[v]) {
                std::cout << neighbor << " ";
            }
            std::cout << std::endl;
        }
    }

private:
    int V; // 顶点数
    std::vector<std::vector<int>> adj; // 邻接表
};

int main() {
    Graph g(5); // 创建一个具有5个顶点的图

    // 添加边
    g.addEdge(0, 1);
    g.addEdge(0, 4);
    g.addEdge(1, 2);
    g.addEdge(1, 3);
    g.addEdge(1, 4);
    g.addEdge(2, 3);
    g.addEdge(3, 4);

    // 打印图的邻接表
    g.printGraph();

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

运行结果：

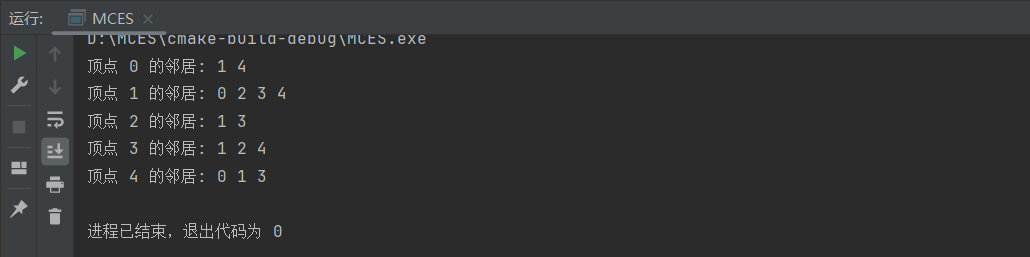
练习题：

1. 解释图的基本概念中的顶点和边。

2. 什么是有向图和无向图？可以给出一个实际生活中的例子吗？

3. 描述深度优先搜索（DFS）和广度优先搜索（BFS）的工作原理。

4. 你可以设计一个简单的图，表示你和你的朋友之间的社交关系。使用C++创建这个图并实现DFS或BFS来查找朋友之间的关系路径。

解释图的基本概念中的顶点和边。

• 顶点：顶点也被称为节点，它们是图中的基本元素，代表对象或实体。在社交网络中，每个人可以被表示为一个顶点。

• 边：边是连接两个顶点的线，表示顶点之间的关系。在社交网络中，如果两个人是朋友关系，就可以用一条边来表示这种关系。

什么是有向图和无向图？可以给出一个实际生活中的例子吗？

• 有向图：有向图中，边有方向，表示从一个顶点到另一个顶点的关系是单向的。例如，Twitter中的关注关系就是一个有向图，其中用户A关注了用户B，但不一定反过来成立。

• 无向图：无向图中，边没有方向，表示两个顶点之间的关系是双向的。例如，Facebook的好友关系可以用无向图表示，如果用户A是用户B的好友，那么用户B也是用户A的好友。

描述深度优先搜索（DFS）和广度优先搜索（BFS）的工作原理。

• DFS（深度优先搜索）：DFS从起始顶点开始，沿着一条路径尽可能深入，直到无法继续为止，然后回溯到其他路径。它使用栈数据结构或递归来实现。DFS类似于沿着分支往下走直到底部，然后再返回并探索其他分支。

• BFS（广度优先搜索）：BFS从起始顶点开始，首先访问所有直接相邻的顶点，然后逐层向外扩展。它使用队列数据结构来实现。BFS类似于水波扩散，先探索离起点最近的区域，然后逐渐扩展到更远的区域。

你可以设计一个简单的图，表示你和你的朋友之间的社交关系。使用C++创建这个图并实现DFS或BFS来查找朋友之间的关系路径。

这是一个简单的C++示例代码，一个社交关系图并执行DFS来查找朋友之间的关系路径。请注意，这只是一个示例，实际应用中的社交关系图通常更复杂。

#include 
#include 
#include 

class Graph {
public:
    Graph(int vertices) : V(vertices) {
        adj = std::vector<std::vector<int>>(vertices);
    }

    void addEdge(int v, int w) {
        adj[v].push_back(w);
        adj[w].push_back(v);
    }

    void DFS(int start, int target, std::vector<bool>& visited, std::vector<int>& path) {
        visited[start] = true;
        path.push_back(start);

        if (start == target) {
            // 找到目标，打印路径
            std::cout << "关系路径: ";
            for (int vertex : path) {
                std::cout << vertex << " ";
            }
            std::cout << std::endl;
        } else {
            for (int neighbor : adj[start]) {
                if (!visited[neighbor]) {
                    DFS(neighbor, target, visited, path);
                }
            }
        }

        // 回溯
        visited[start] = false;
        path.pop_back();
    }

private:
    int V; // 顶点数
    std::vector<std::vector<int>> adj; // 邻接表
};

int main() {
    Graph socialNetwork(7); // 创建一个具有7个顶点的社交关系图

    // 添加社交关系边
    socialNetwork.addEdge(0, 1);
    socialNetwork.addEdge(0, 2);
    socialNetwork.addEdge(1, 3);
    socialNetwork.addEdge(1, 4);
    socialNetwork.addEdge(2, 5);
    socialNetwork.addEdge(3, 6);

    std::vector<bool> visited(7, false);
    std::vector<int> path;

    std::cout << "查找朋友之间的关系路径:" << std::endl;
    socialNetwork.DFS(0, 6, visited, path); // 查找从顶点0到顶点6的关系路径

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

运行结果：

注意：这个示例代码演示了如何创建一个社交关系图，并使用DFS来查找朋友之间的关系路径。实际应用中，社交网络可能包含更多顶点和更复杂的关系。