關聯式資料庫模型The relational data model

RELATIONAL MODEL關係模型

• 結構化查詢語言（SQL）基礎
  foundation of structured query language (SQL)

• 許多資料庫設計方法的基礎
   foundation of many database design methodologies

• 資料庫研究基礎
  foundation of database research

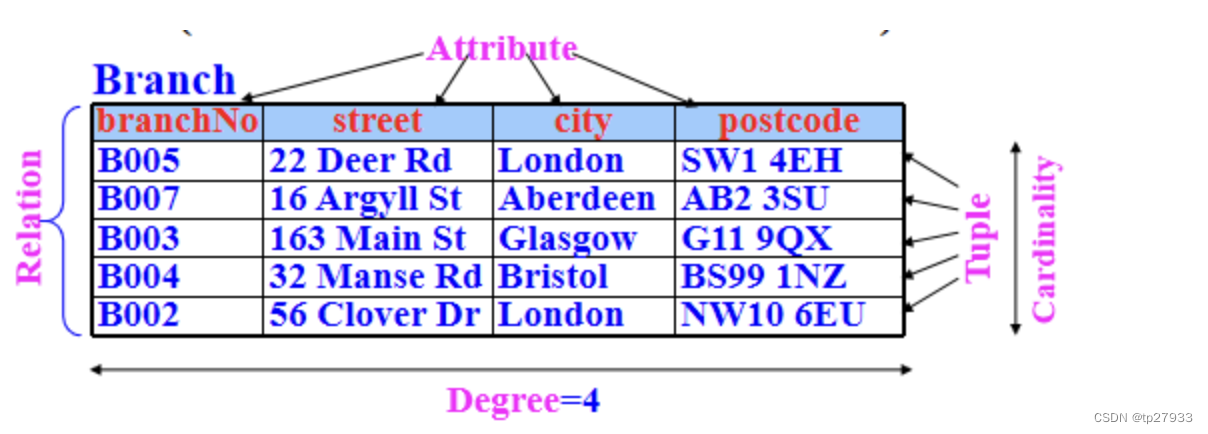
關係(Relation)

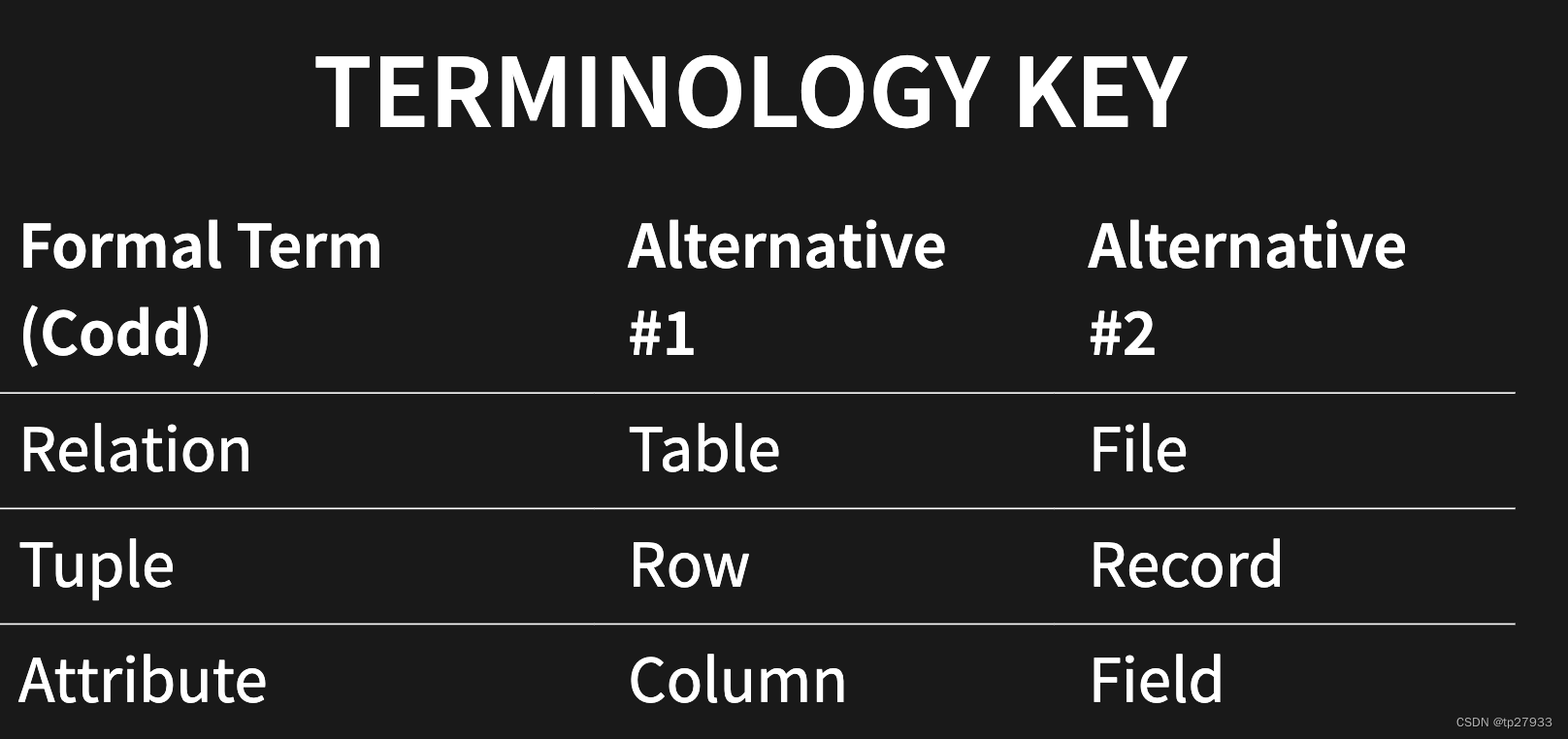
關係是一個有列和行的表格 Relation is a table with columns and rows 又稱為table或是file.

關係是無序的，且為域列表的笛卡爾積的命名子集

笛卡兒積 笛卡兒積

給定一組域D1,D2,…,Dn（它們可以有相同的元素，即可以完全不同，也可以部分或全部相同）。D1,D2,…,Dn的笛卡爾積為D1×D2×。 ..×Dn={(d1, d2, …, dn)|di∈Di，i=1,2,…,n}
由定義可以看出，笛卡爾積也是一個集合。

關係性質PROPERTIES OF A RELATION

• 區別於其他關係的名稱（獨一）

• 沒有重複的元組

• 元組中的性質是原子的（不能有合集或多個值）

• 屬性的值來自單一域

• 不允許組合資料類型的操作

• 每個屬性都有一個不同的名稱(單一)

• 屬性和元祖都是無序的

域 (domain) ：

允许的属性取值构成的集合，属性的取值范围)，例如： WorkDay is the set of {Mon,Tue,Wed,Thu,Fri,Sat,Sun} , 又或者「性別」屬性的內含值，必須是「男生」或「女生」。員工號碼的資料型態 (Data Type) 可 能為 CHAR(9)，表示該值域之範圍是在 9 個字元長度以內。年齡只允許正整數等等...關係是一個有列和行的表格 Relation is a table with columns and rows 又稱為 

原子域 (atomic domain)：

所有的域都是原子資料（Atomic Data）。例如整數、字串是原子數據，集合、堆疊屬於非原子數據，第一模型關係的這種限制稱為範式（1NF）條件

屬性（ATTRIBUTE）

描述事物的一些特徵稱為屬性。例如學號、姓名、職位、年齡等。又稱為column or field

元組（Tuple）

是關係的一行(row)。又稱為 row 或是 record

度、目(Degree) 

is the number of attributes in a relation(属性数)

實體關係模型(ENTITY RELATIONSHIP MODEL)

實體之間的關係、關聯，保存特定資訊的實體、表

實體（ENTITY）：

• 是指用以描述真實世界的物件。也可以是邏輯抽象的概念（例如帳號、工作）
• 必須可以被識別，亦即能夠清楚分辨出兩個不同的實體。
• .實體都是以「名詞」的型式來命名，不可以是「形容詞」或「動 詞」。

弱實體(weak entity) 

• 必須依靠其他實體才能存在

• 其主鍵包括父實體的主鍵 ，例如LineItem 或 OrderItem - 取決於對應的產品

強實體(strong entity) 

• 不依靠其他實體存在

• 沒有外鍵或外鍵可以為空的關係，例如Product relation

強實體與弱實體的連結只能是1：1或1：N

實體又可分為實體集合 ( Entity Set )、實體類型 ( Entity Type ) 與 實例 ( Instance )。

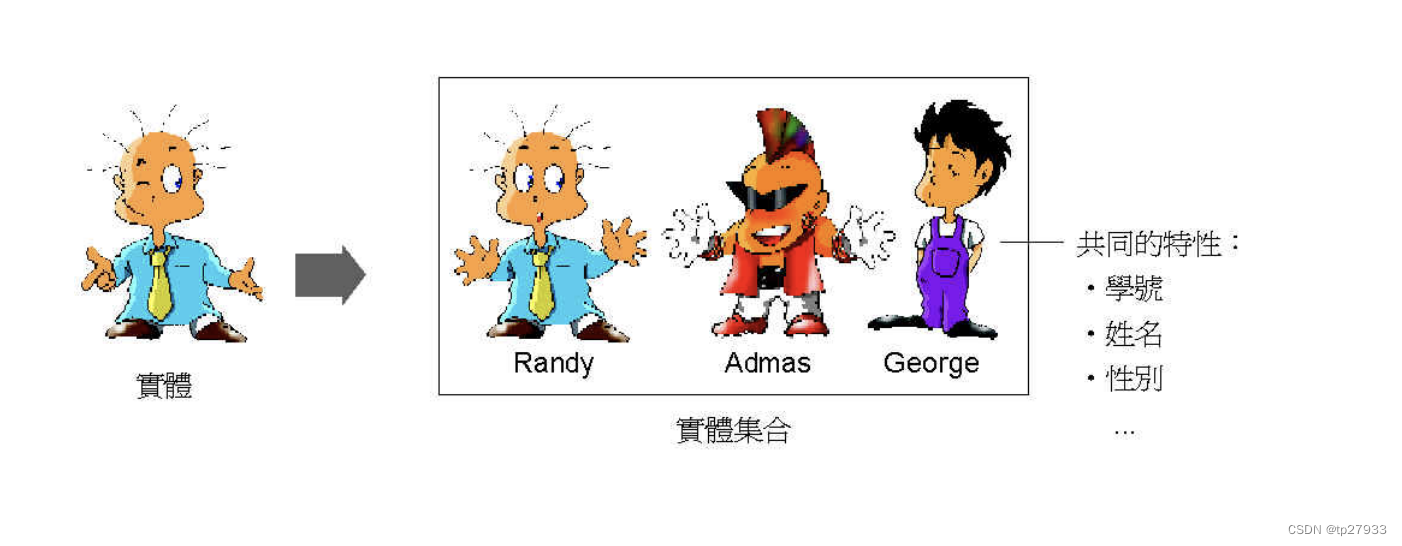
實體集合 (Entity Set)

它們都 具有相同的特性

實體類型 (Entity Type)

例如將 上圖的實體集合稱為學生實體類型 (Entity Type)

實例 (Instance)

而 Randy 、Admas 及 George 就稱為 學 生實體類型中的實例 (Instance) 。

屬性（ATTRIBUTES）

用來描述實體的性質(Property) (Property)。屬性具有名稱、關聯實體、合法值域（ domain of legal values）

屬性類型

• 簡單屬性 simple attributes
• 複合屬性 composite attributes
• 多值屬性 multivalued attributes

簡單屬性

已經無法再繼續切割成其他有意義的單位，亦即該屬性為 基元值(Atomic Value) 

【例如】「學號」屬性便是「簡單屬性」。 「地址」就不算是簡單屬性，因為它還可以再切割成區域號 碼、 縣市、鄉鎮、路、巷、弄、號等小單位。

複合屬性 composite attributes

由兩個或兩個以上的其他屬性的值所組成。

【例如】 「地址」屬性是由區域號碼、縣市、鄉鎮、路、巷、弄、號等 各個屬性所組成。

【適用時機】戶政事務查詢，房屋仲介網站… 那些屬性是屬於「複合屬性」呢？必須要視需求而定。一般使用者在 設定客戶資料表或學生資料表時， 「地址」屬性是視為「簡單屬性」。 【優點】大量查詢時，較快速。 where 地址 Like ‘*苓雅區*’速度較慢 where 區域=‘苓雅區’ 速度較快

多值屬性 multivalued attributes

屬性值可能不只一個時，比如一張唱片的作曲人，可能有ABC、CDF

衍生屬性 (Derived attributes)

是指它的值可以由其它屬性之值經由某種方式的計算或推論而獲得的。例如：「年齡」、 「星座」可由生日推算出來。因此又稱為推導屬性。它可以不用實際存於資料庫中。

值key

• 候選鍵 Candidate Key
• 複合鍵 Composite Key
• 主鍵 Primary Key
• 次要鍵 Secondary Key
• 交替鍵 Alternate Key
• 外鍵 Foreign Key
• 自然鍵 Natural Key
• 代理鍵 Surrogate Key

候選鍵 Candidate Key

候選鍵就是主鍵的候選人，並且也是關聯表的屬性子集所組成。

一個屬性(欄位)是要成為候選鍵，則必須同時要符合下列兩項條件：

        1.具有唯一性 是指在一個關聯表中，用來唯一識別資料記錄的欄位。 例如：超鍵(Super Key) (Super Key)。但可以是由多個欄位組合{縣市+區域}而 成。

        2.具有最小性 是指除了符合「唯一性」的條件之外，還必須要在該「屬性子集」中 移除任一個屬性之後，不再符合唯一性。亦即鍵值欄位個數為最小。 例如： {縣市+區域}組合成來符合「唯一性」的條件。並且在移除任 一個屬性{區域}之後， {縣市}不再符合唯一性。

若候選鍵只包含一個屬性時，稱為簡單(simple) (simple)候選鍵。 例如： {學號} 若包含兩個或兩個以上屬性時，稱為複合(composite) (composite)候選鍵。 例如： {縣市+區域}

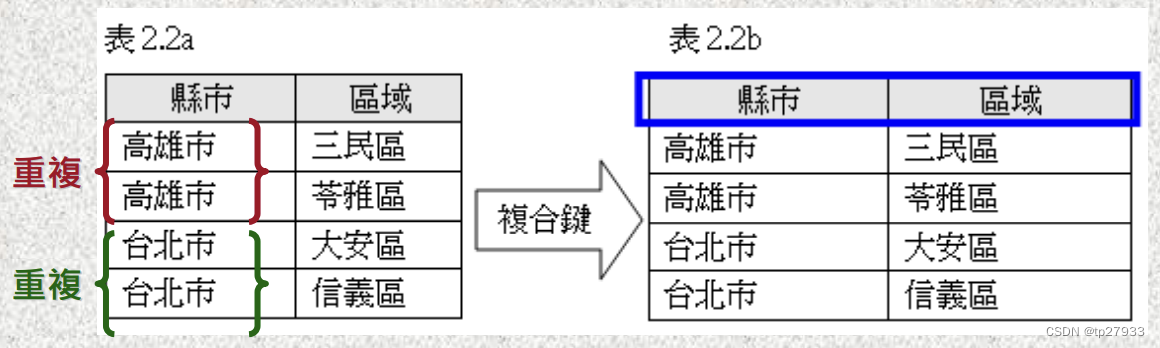
複合鍵 Composite Key

是指資料表中的主鍵，是由兩個或兩個欄位以上所組成，這種 主鍵稱為複合鍵(Composite Key) (Composite Key)。 當表格中某一欄位的值無法區分資料記錄時，可以使用這種方法。

例如：

在表2-2a中「縣市」的欄位值有重複，無法區分出每一筆記錄，所以 「縣市」欄位不能當作主鍵欄位。因此，必須要把「縣市」與「區域」 兩個欄位組合在一起，當作主鍵欄位。如表2-2b所示。

主鍵 Primary Key

是指用來識別記錄的唯一性，它不可以重複及 空值(Null)。

次要鍵 Secondary Key

主要的功能是提供資料索引。資料庫系統中，除了主鍵這個唯一的識別值，可以用做索引外，也可以設定其他欄位用作資料索引，這類的鍵值並不是主鍵，但因為資料內容並不會重複，所以也可作為資料索引，這就是次要鍵。

交替鍵 Alternate Key

在一個關聯中，只有一個主鍵，若候選鍵未被選為主鍵時，則稱為 「交替鍵(Alternate Key) (Alternate Key)」。

自然鍵 Natural Key

又稱為商業鍵 (Business Key) 或domain key，是由人可以識別並且帶有一定商業 含義的屬性所組成。例如：身分證號碼，如果保證是唯一，可以被選定為自然鍵，用於確 定一個人。員工實體的(姓名，性別，生日，地址) 四個自然的屬性也可以被選為不重複的 複合主鍵。但是，相同的實體在不同的公司系統中可能會有不同的自然鍵。

容易有問題，例如規則改變時，例如假設名字跟生日是作為員工的自然鍵是ok的但是當雇用越來越多人時會出現同樣的名字跟生日

代理鍵 Surrogate Key

又稱為 synthetic key 或 pseudokey。即時商業規則改變也較穩定。

是在當實體中沒有明顯的候選鍵，或是候選鍵都不適合當主鍵時，例如，屬性資料太長， 或屬性太多，或屬性太複雜，或屬性意義層面太多，或有性能問題 (Performance Issue)， 就會利用一個沒有商業意義的但唯一的字段來代替作為主鍵。

代理鍵值通常是由資料庫管理系統產生的。Sybase 和 SQL Server 用 Identity Column。 Oracle 用 SEQUENCE。它可以自動產生唯一的遞增序列整數 (Unique Sequences Integer) 。 另一種技術是寫一個 ID 產生程序 (Universal Identity Generator) ， 它可以自動產生唯一的 序列整數，也可以產生唯一的隨機整數 (Unique Random Number) 。 代理鍵值沒有商業意義，因此一般來說，不顯示給使用者看，也不顯示在表單與報表中。 但是程序設計師在寫應用程序時，常常用它來連接多個資料表 (Tables Join) 來得到資料。

外鍵 Foreign Key

是指用來建立資料表之間的關係，其外鍵內含值 必須要與另一個資料表的主鍵相同。

關係類型RELATIONSHIP TYPES

• 一對多 One to many (1:M)
• 一對一 One to one (1:1)
• 多對多 Many to many (M:N)
• Unary (Recursive)
• Ternary

一對多 One to many (1:M)

一對多的關係(1：M)：表示兩個實體之間的關係是一對多的關係。

【舉例】假設每一位教授可以同時指導多位研究生，但每一位研究生只 能有一位指導教授，不可以有共同指導現象。

【說明】：每一位教授可以指導多位研究生，但每一位研究生只能有一位指導教授。

一對一 One to one (1:1)

表示兩個實體之間的關係是一對一的關係。

【舉例】假設每一位老師僅能分配一間研究室，並且每一間研究室只能 被一位老師使用。

多對多 Many to many (M:N)

表示兩個實體之間的關係是多對一的關係。

【舉例】一名員工負責多個專案； 一個專案有許多員工參與其中

遞迴 Unary (Recursive)

二元關係中如果關係兩端的個體為同一個體（有些二元關係型態的左右兩邊實體型態是相同，只是扮演不同角色），則我們稱. 為遞迴關係(Recursive relationship)

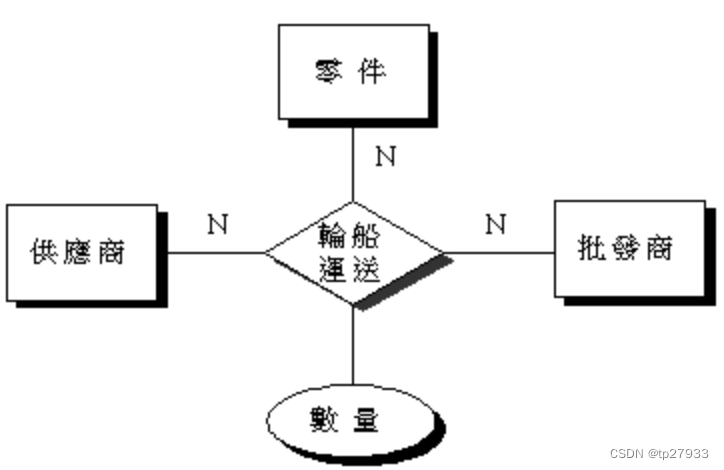
【舉例】零件、供應商與批發商均是實體類型，三者間有「輪船運送」之關係，且數量為輪船運送關係之屬性。

• 某些供應商以輪船運送某些數量之零件給某些批發商，每一實體都有多個案例參與。
• 「數量」是某一特定零件從某一特定供應商用輪船運送到某一特定批發商之數量。

【舉例】每個員工都有一個經理，而經理也是一個員工

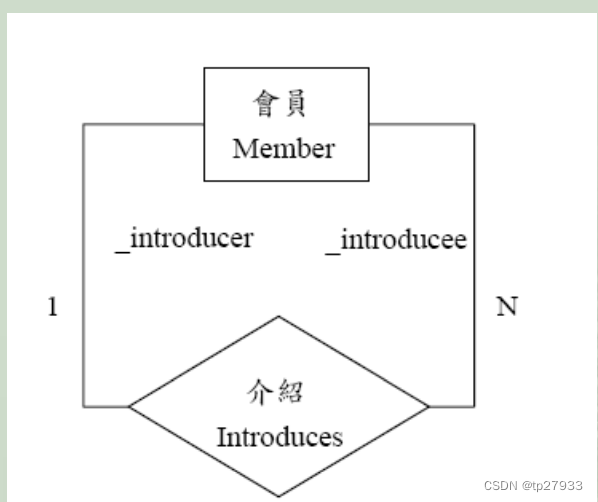
【舉例】介紹人的會員或被介紹的會員，均是 會員，但扮演不同的角色（role）

Ternary

三個實體類型其案例間之共同關係，此關係中每個實體類型可能有一或多個案例參與。

實體完整性規則 INTEGRITY RULES

• Domain Integrity
• Entity Integrity
• Referential Integrity

值域完整性規則(Domain Integrity Rule)

指在單一資料表中，同一資料行中的資料屬性必須要相同

實體完整性規則 Entity Integrity

在單一資料表中，主索引鍵必須要具有【唯一性】並且也不可以為空值 (NULL)。

參考完整性規則 Referential Integrity

在兩個資料表中，次要資料表的外鍵(FK)的資料欄位值，一定要存在於主要資料表的主鍵(PK)中的資料欄位值。

企業限制 ENTERPRISE CONSTRAINTS

超出基本完整性約束的附加規則

【舉例】

1. 一個班級最多有30名學生
2. 一位講師最多教授 4 門課程
3. 員工的薪水不能超過其經理的薪資

商業規則 BUSINESS RULES

在需求收集過程中發現的其他規則

【舉例】並非所有講師都授課

http://cc.cust.edu.tw/~ccchen/doc/db_03.pdf

基數和連接性 CARDINALITY AND CONNECTIVITY

連接性CONNECTIVITY

連接性是兩個表之間的關係 

【舉例】一對多 或 多對多 

• 連接性可以是 0、1 或多個

• 基數和連通性在「魚尾紋」（crow's foot）圖中一起表示

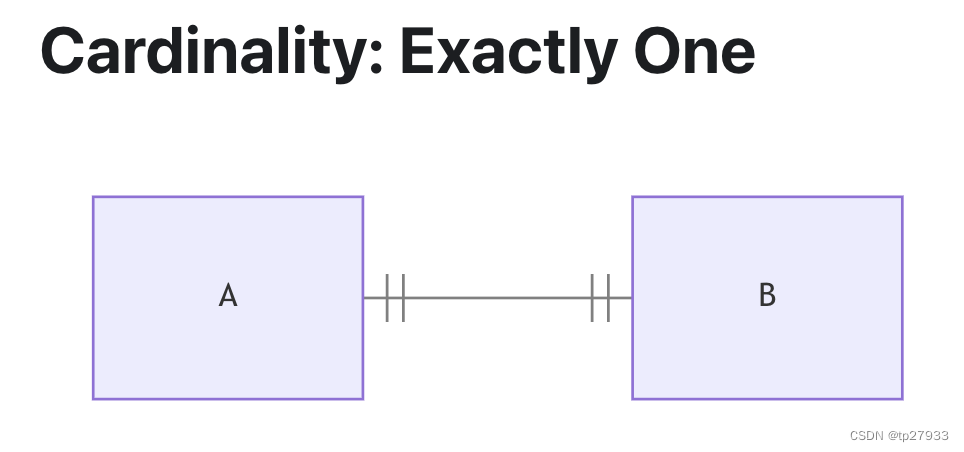
基數 CARDINALITY

特定於相關實體出現的最大和最小數量的業務規則

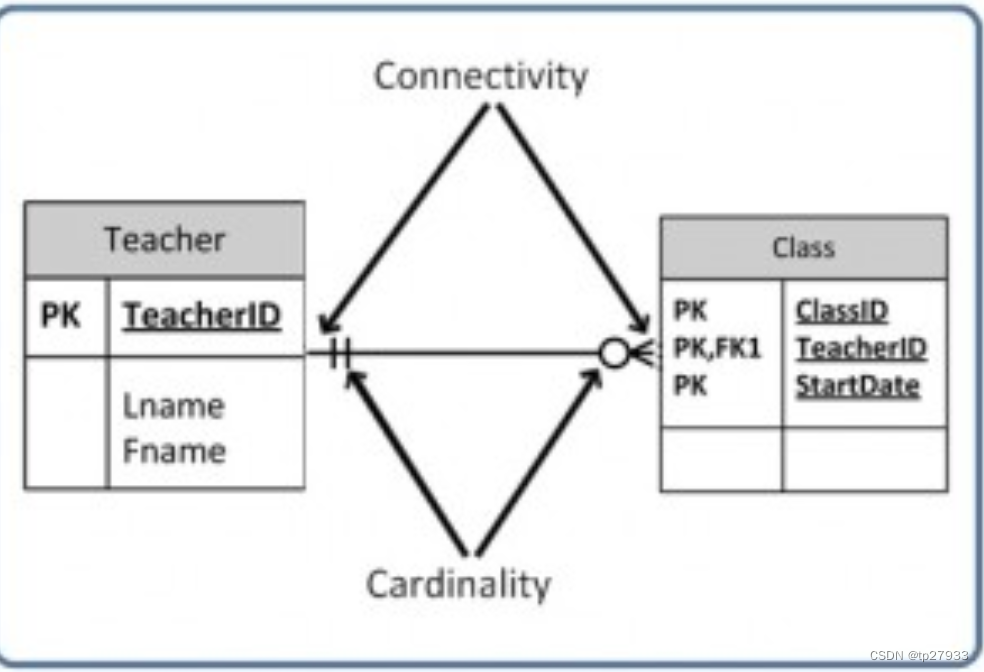
關係類型 Relationship Types

• 可選關係 Optional relationships

• 強制性關係 Mandatory relationships

• Non-Identifying Relationships

• Identifying Relationships

Identifying Relationships

Identifying Relationships 是指子表(child table)的每一列資料必須依賴於母表(parent table)的資料而存在。母表的主鍵(primary key)欄位必須為子表的主鍵的一部分

例如一個人(PERSON)有多支電話號碼(PHONE_NUMBER)，兩者是一對多的關係如下。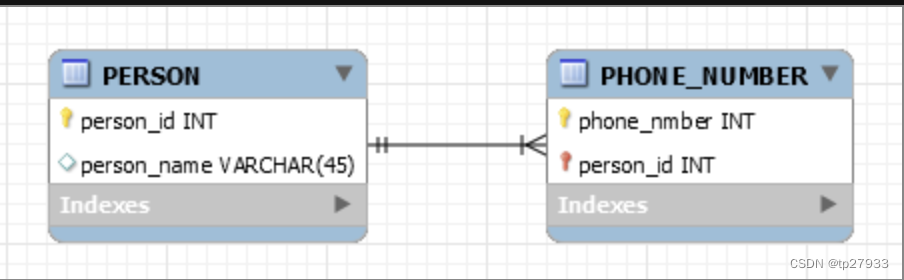

PHONE_NUMBER的主鍵除了電話號碼(phone_number)本身外，還必須加上外鍵(foreign key)人的編號(person_id)來組成。如果人不存在，當然就沒有屬於那個人的電話號碼。子表(PHONE_NUMBER)的一列資料必須依賴於母表(PERSON)的資料而存在，這就是Identifying Relationships，兩實體間的關係強烈。

Non-Identifying Relationships

Non-Identifying Relationships 是指子表的資料必須不依賴於母表的資料而存在。母表的primary key欄位不為子表primary key的一部分。

例如一個團體(GROUP)可有多個人(PERSON)，兩者是一對多的關係如下。

人(PERSON)可以不屬於任何團體，一個人的存在與否與團體是否存在無關，PERSON的團體編號(group_id)雖然是參照GROUP的外鍵，但不屬於PERSON主鍵的一部分。子表(PERSON)的一列資料不依賴於母表(GROUP)的資料而存在，這就是Non-Identifying Relationships。而兩實體的關係可以是選擇性或強制的，差別在於外鍵欄位是否允許null。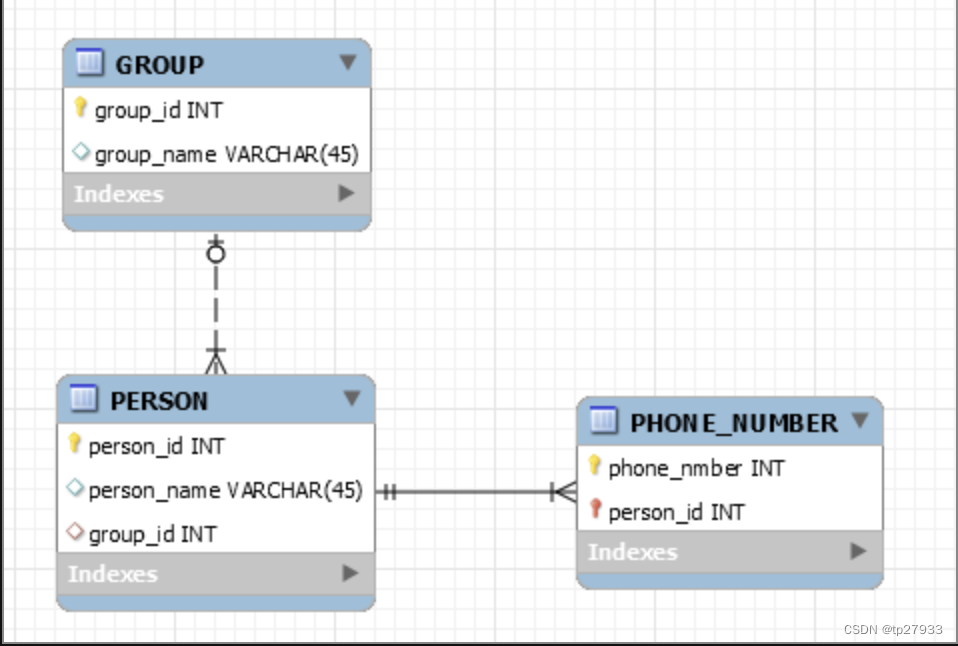

可選關係 Optional relationships

解釋為零或多個

下圖的關係表可以解讀為：

• 左側：訂單實體必須至少包含 Customer 表中的 1 個相關實體 （符號：|），最多包含 1 個相關實體（符號：|），由右到左

• Right side: 右側：顧客最少可以有零個訂單，最多可以下多個訂單。

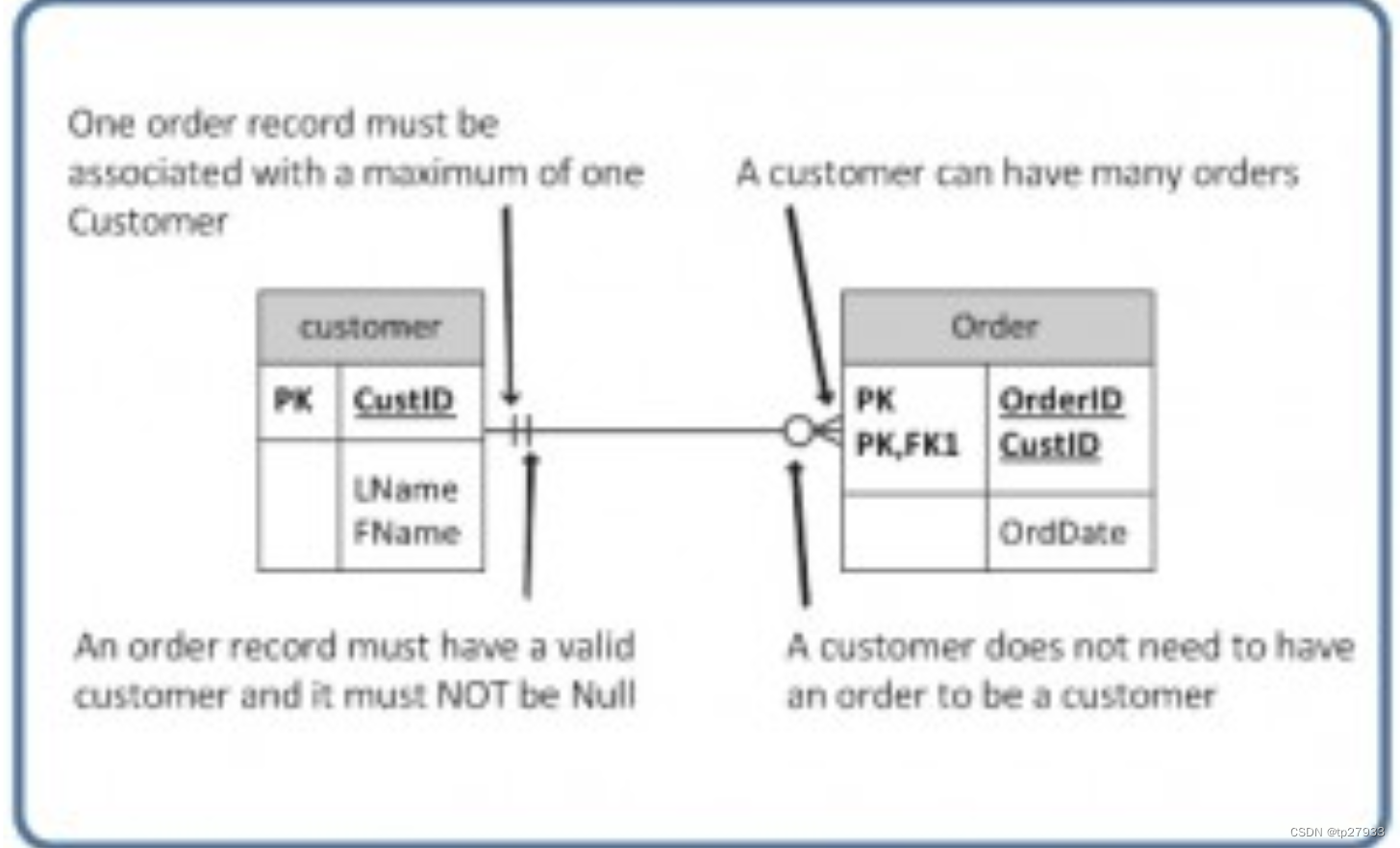
意思是零或一。一側是可選的。

強制性關係 Mandatory relationships

下圖的關係表可以解讀為： 

• 左側：最小 1 和最大 1

•   右側：最小 1 和很多。

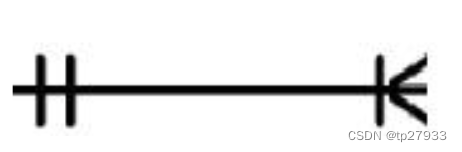
一對一的符號 。一側是強制性的。
 

一對多關係符號。多方是強制性的。

可以是0個也可以是多個。連接性可以是多個或是一個

下圖，連接性不能為 0（零），連接性只能是1。

範例

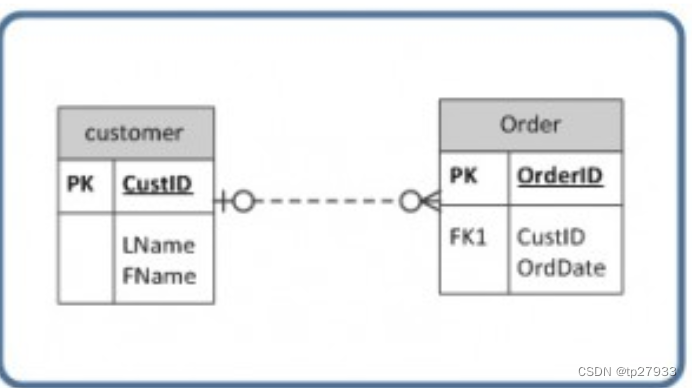
• Order 表中的 CustID 必須在 Customer 表中找到，最少 0 次，最多 1 次。 0 表示 Order 表中的 CustID 可能為空。
• 最左邊的 1（就在代表連通性的 0 之前）表示如果 Order 表中存在 CustID，則它只能在 Customer 表中出現一次。此時可以推斷： Order 表中的 FK 允許為空，且 FK 不是 PK 的一部分，因為 PK 不得包含空值。

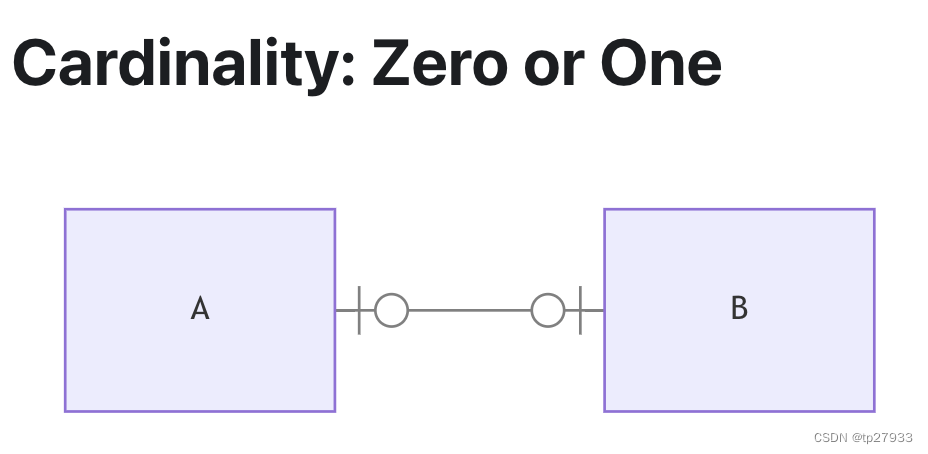
A在B中出現一次或0次（Ｂ對於A也相同） 

A在B中出現一次且只有一次（Ｂ對於A也相同）  

A在B中出現0次或多次（Ｂ對於A也相同） 

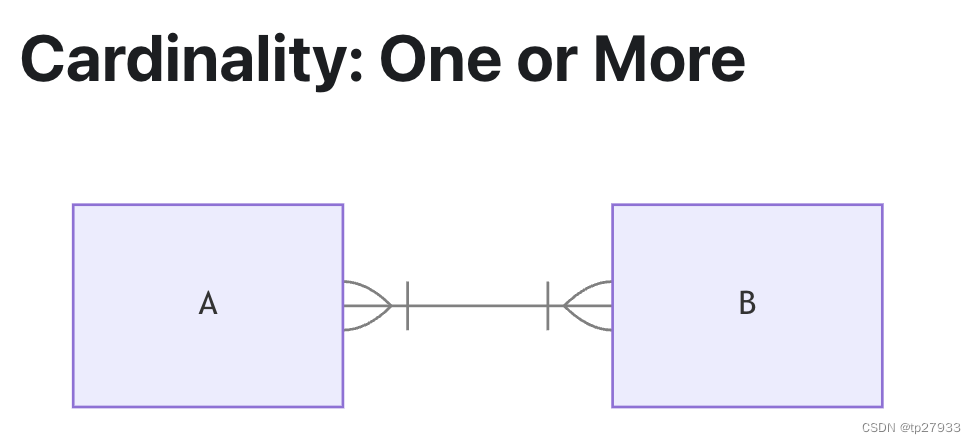 A在B中出現1次或多次（Ｂ對於A也相同） 

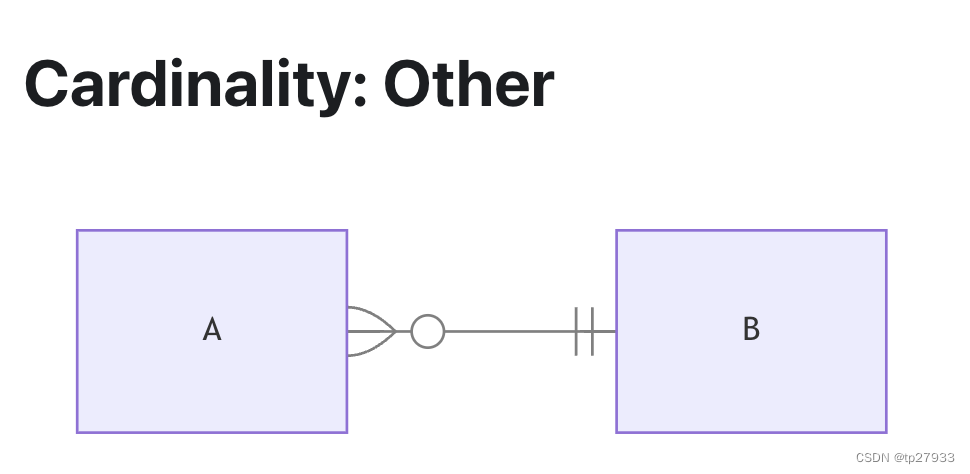A在B中出現1次且只有一次

B在A中出現0次或多次

命名方式

• ERD最好要有一個命名的慣例，成為寫的人和讀 的人的一個共同的默契
•  實體型態及關係型態的名稱的第一個字元為大寫字母
•  屬性的名稱第一個字元為小寫字母 Z 角色名稱第一個字元要底線(underscore)_。
•  實體型態的名稱用單數名詞
•  關係型態的名稱用單數動詞
•  屬性的名稱盡量用不同的名詞。
•  在畫ERD時內容文字要盡量符合人的讀書習慣，例如： A 實體 → 關係→ B實體，要讓看的人由左而右或由上 而下很像在看一句話一樣。

ER Modelling

主要就是由實體(Entity)和關係(Relationship)所構成的資料模型

正規化理論

「正規化理論」(Normalization theory)目的是使關聯式資料庫的設計能讓資料重複性與相依性能夠降到最低，因為重複的資料會浪費磁碟空間，並產生維護方面的問題，不一致的相依性則會讓資料出錯誤，以下是錯誤的說明：

• 資料重複 Relational Design and Redundancy
• 新增異常 Insertion Anomaly
• 修改異常 Update Anomaly
• 刪除異常 Deletion Anomaly
• Avoiding Anomalies

資料重複 Relational Design and Redundancy

如果資料有多筆重複，可能產生資料不一致的情形。

解決方法為將欄位細分至不同table來減少Redundancy的問題

例如：同樣的使用者為alice但是生日卻不一致

新增異常 Insertion Anomaly

例如：產品的單價欄位設計在訂單資料表中，且訂單標號為此資料表的主鍵，則未接單時，產品價格無法輸入。

刪除異常 Deletion Anomaly

刪除資料表中的某筆資料，可能也把一些重要欄位的資料也一併刪除。或者已刪除的記錄是唯一包含實體資訊的記錄，該資訊將永遠遺失。

例如：把紀錄跟使用者放在同一個table裡，當紀錄被刪除，該使用者的資料全無。

修改異常 Update Anomaly

例如：某項目的價格變更，在修改時，由於有資料重複的現象，必須做多筆資料的更新才能完全修改。

避免異常狀況Avoiding Anmales

• 將大的table切分為小table，而此過程稱為正規化 normalizaion
• 減少多餘
• 使用功能依賴

功能相依 FUCTIONAL DEPENDENCIES

假如 R 代表一個關聯表，X 與 Y 為 R 的屬性的子集合。若且唯若(If and only if) R 的 X 值可以唯一決定 Y 的值時，稱為“Y 功能相依於 X”(Y is functionally Dependent on X) 或稱為“X 功能決定 Y”(X funtionally determines Y)，以 X→Y 表示。換另一種說法：若且唯若對於 R 中的每一個 X 值，都有唯一的 Y 值與其對應。

學生選課資料中包括學生學號(Sno)、課程代號(Cno)、學分數(Credit) 與成績(Score)。其功能相依性 FD 如下：

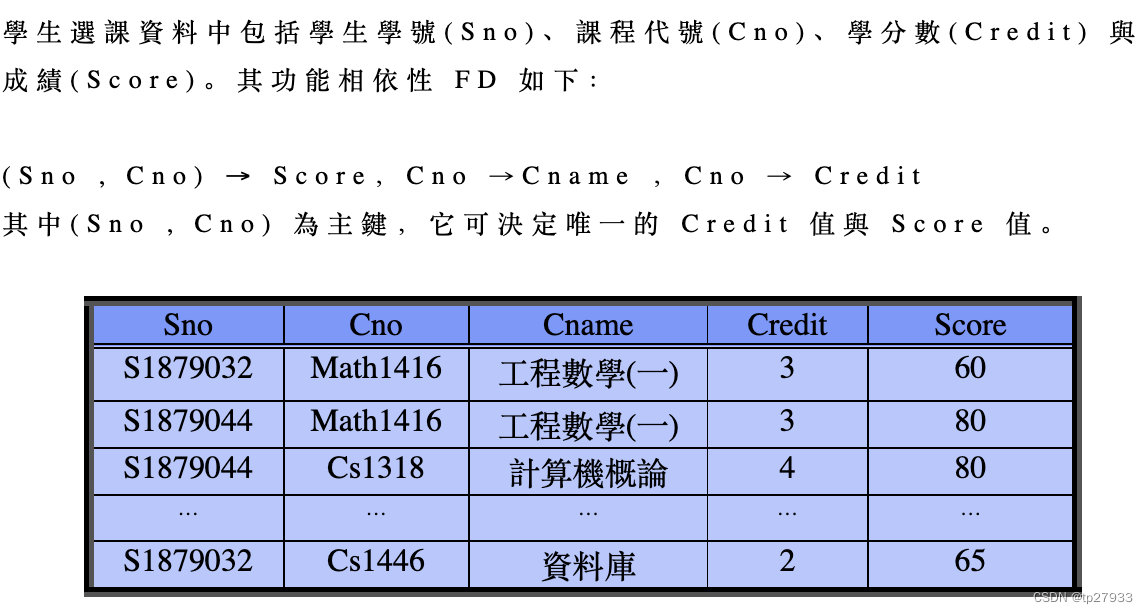
若 X→Y 時，X 稱為功能相依決定者(determinant)，Y 則稱為功能相依者(Dependent)。
值得注意的是，如果 X 是關聯表 R 中的候選鍵 (或是主鍵)，則 R 中所有的屬性必須功能相依於 X。如例 1 中，所有的屬性都功能相依於主鍵(Sno , Cno)。

Armstrong's Axioms

推導規則 Rule Of Inference

• Axiom of reflexivity
• Axiom of augmentation
• Axiom of transitivity
• Union
• Decomposition

反身性(Reflexivity)：

若 B 是 A 的子集合，則 A→B。

擴增性(Augmentation)：

若 A→B，則 AC→BC。

遞移性(Transitivity)：

若 A→B，且 B→C 則 A→C。

以上三個定理可利用功能相依性的基本定義來證明，稱為基本定理。

聯合性 Union

若 A→B 且 A→C 則 A→BC。

分解性 Decompositon

為聯合性(Union)的相反。若 A→BC 則 A→B 且 A→C。

虛擬遞移性(Pseudotransitive)：

若 A→B 且 BC→D 則 AC→D。

以上的定理，可利用阿姆斯壯定理的基本定理證明，稱為衍生定理。

正規化

規範化是識別表格設計中冗餘程度的過程，然後對表格進行劃分以糾正它。我們可以使用函數依賴性來評估表格處於哪一個正規形。

將原先關聯表格的所有資訊，在分解成其他表格後，仍可以透過「合併」新關聯表格的方式得到相同的資訊，亦為「無損失分解」（Lossless Decomposition）

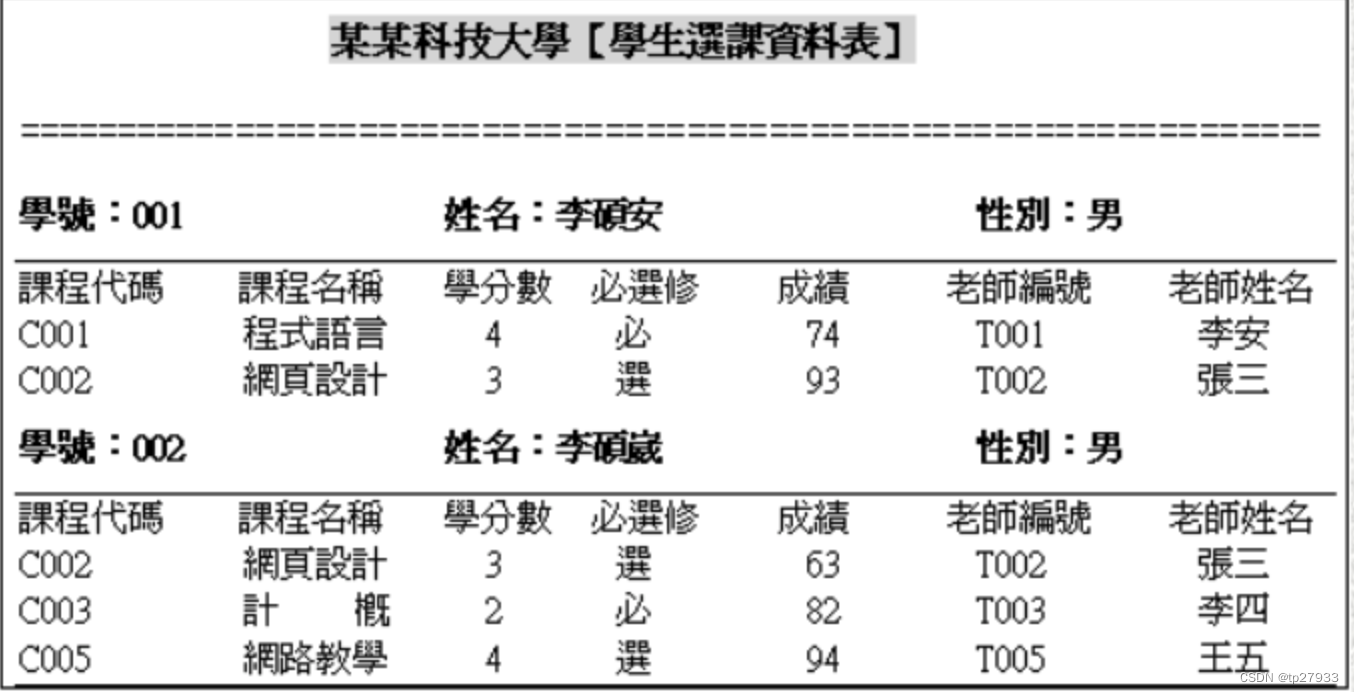
不當設計的影響

• 新增異常：
  • 新增學生，但未選課
  • 新增課程，但未被選課
  • 新增老師，但未授課
• 刪除異常：
  • 刪除課程時，學生的成績資料遺失
• 更新異常：
  • 更新課程資料時，需一次修改多筆資料
  • 更新老師資料時，需一次修改多筆資料

第一正規化（1NF）

定義

1. 要排除重複群的出現，要求每一列資料的欄位值都只能是單一值（基元值）。a relation is in 1NF if it has no mulit-valued attributes
2. 沒有任何兩筆以上的資料完全重複。
3. 資料表中需有主鍵（唯一值），其他所有欄位都相依於主鍵。
4. 同一張資料表內，不建議用多個欄位表達同一個事情（如下圖）。

未符合第一正規化

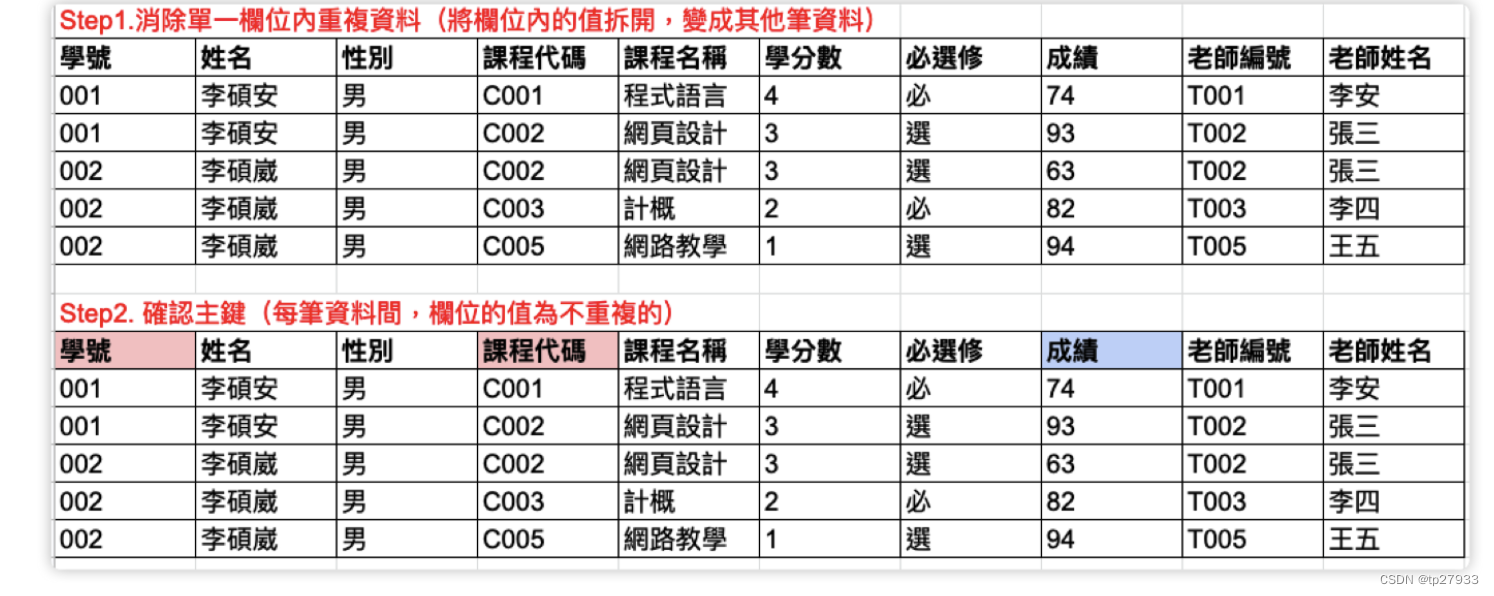
第一正規化作法

1. 確認是否有重複表達的欄位。
2. 將欄位內重複的資料分別存為不同的Data Row資料。

第二正規化（2NF）

定義

1. 符合1NF。
2. 消除「部分功能相依 Functional Dependencies」，每一個非鍵欄位必須完全相依主鍵（學號=>學生，課程=>學分…），通常「主鍵有多個欄位」組成時會發生「部分功能相依」。如果主鍵為學號+年級，此時學號 => 學生時並不符合第二正規化，因為學號決定學生但是學號只是一部分的主鍵。

來複習下部分功能相依的意思

• • 若Z 亦可由複合屬性 {X, Y} 決定，但 {X, Y} 中僅需X 即能決定Z，則稱Z 部分功能相依 (Partial Functional Dependency) 於複合屬性 {X, Y} 。

作法

1. 檢查是否存在「部分功能相依」（可從多個欄位組成的主鍵開始檢查）。
2. 將「部分功能相依」的欄位分割出去，另外組成新的資料表。

符合第一正規化但尚未第二正規

主鍵是由「學號」與「課程代碼」組成：

• 姓名、性別，相依於 「學號」
• 課程名稱、學分數、必選修、老師編號、老師姓名，相依於「課程代碼」

存在「部分功能相依」，需要將部分功能相依欄位分割（2NF），以下為分割後結果

發現「重複的資料」，因為需符合1NF，所以將重複的資料去除

第三正規化（3NF）

定義

1. 符合2NF。
2. 各欄位之間沒有存在「遞移相依」的關係，也就是與「主鍵」無關的相依性。

來複習下遞依相依

• 若關聯表存在功能相依X→Z，又存在X→Y 與Y→Z，而且Y 不是關鍵屬性，則稱X→Z 為遞移相依 (Transitive Dependency)。

作法

1. 檢查是否存在「遞移相依」的欄位。
2. 將「遞移相依」的欄位分割出去，另外組成新的資料表。

• 「老師編號」相依於「課程代碼」而且「老師姓名」相依於「老師編號」，所以「老師姓名」與「課程編號」（主鍵）為無關的相依。
• 「老師姓名」與主鍵存在著「遞移相依」的關係。

Boyee-Codd正規化（BCNF）

視情況使用，實務上大多都只會做到3NF。如果資料表的主鍵只由單一欄位組成, 則符合 第三階正規化的資料表, 亦符合 Boyce-Codd 正規化。當一個表有多個候選鍵時，即使關係是3NF的，也可能導致異常。Boyce-Codd範式是3NF的特例。且僅當每個行列式都是候選鍵時，關係才屬於BCNF。

定義

• 3NF的改良式(必須滿足3NF)。
• 主鍵中的各欄位（單獨看）不可以相依於其他非主鍵的欄位。

作法

1. 確認由多個欄位組成的主鍵是否有其他欄位相依於主鍵中的每個欄位。
2. 如有獨立相依的情況，新增一個獨立的主鍵欄位。

確認資料表是否都有符合BCNF

• 學生資料表
  • 3NF
  • 單一主鍵
  • 符合BCNF
• 課程資料表
  • 3NF
  • 單一主鍵
  • 符合BCNF
• 老師資料表
  • 3NF
  • 單一主鍵
  • 符合BCNF
• 成績資料表
  • 3NF
  • 主鍵由兩個欄位組成，但：
    • 成績相依於「學號」及「課程代碼」欄位
    • 成績未相依於「學號」（必須要有課程代碼才知道是哪堂課的分數）
    • 成績未相依於「課程代碼」（必須要有學號才知道是誰的分數）

符合BCNF

BCNF例子1

​​​​​​​

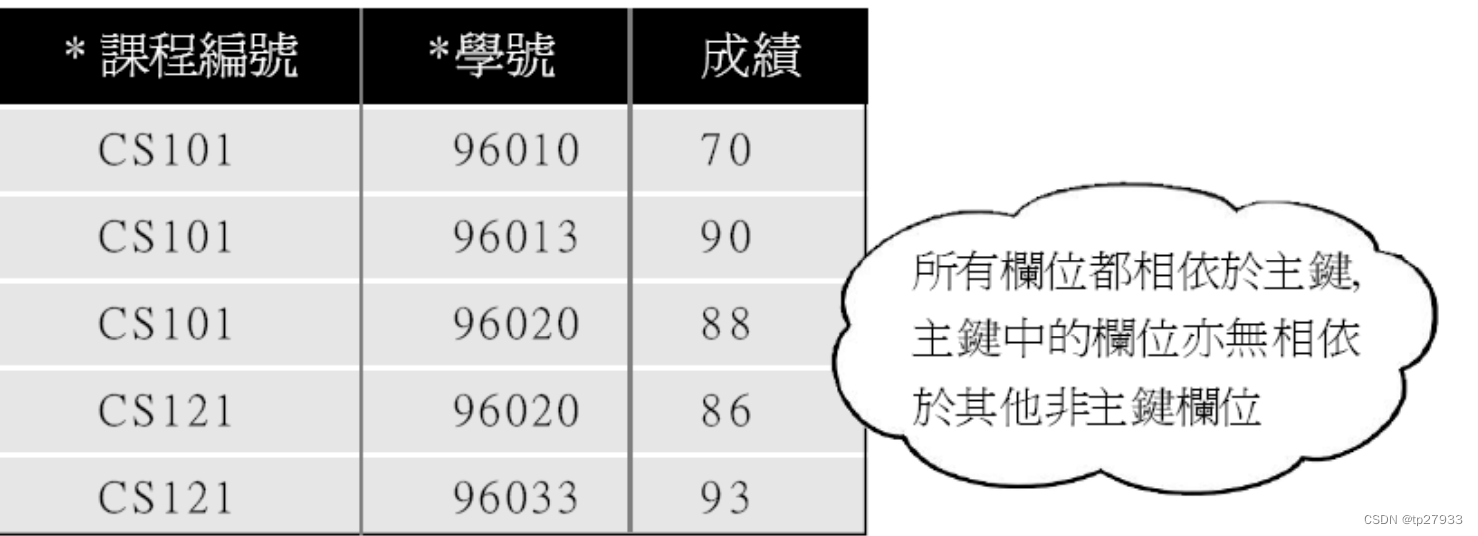
檢驗『成績』資料表是否滿足 BCNF 規範

成績欄相依於課程編號及學號欄, 對課程編號 欄而言, 並無相依於成績欄；

對學號欄而言, 也 無相依於成績欄。 

所以成績資料表是符合『Boyce-Codd 正規化 的形式』的資料表。 

BCNF例子2

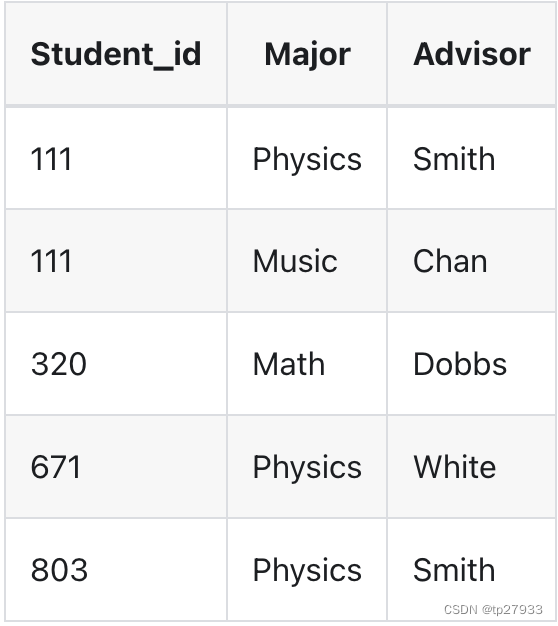
以下為商業規則：

1. 每個學生可以主修多個科目
2. 對於每個專業，一名學生只有一名顧問。
3. 每個專業都有多名顧問
4. 每個顧問只建議一個專業
5. 每位顧問為一個專業的多名學生提供建議。

以下是功能相依性

1. Student_id, Major => Advisor
2. Advisor => Major

這樣的結構下，可能會產生以下的異常(Anomalies)

1. 刪除 Delete – 學生刪除導師訊息
2. 新增 Insert – 新顧問需要一名學生
3. 更新 Update – 不一致(inconsistencies)

Note: 沒有單一一個屬性是候選鍵

主鍵PK 可能是： Student_id, Major 或者 Student_id, Advisor.

作法（解決）

建立以下兩個表 table

1. St_Adv (Student_id, Advisor)
2. Adv_Maj (Advisor, Major)

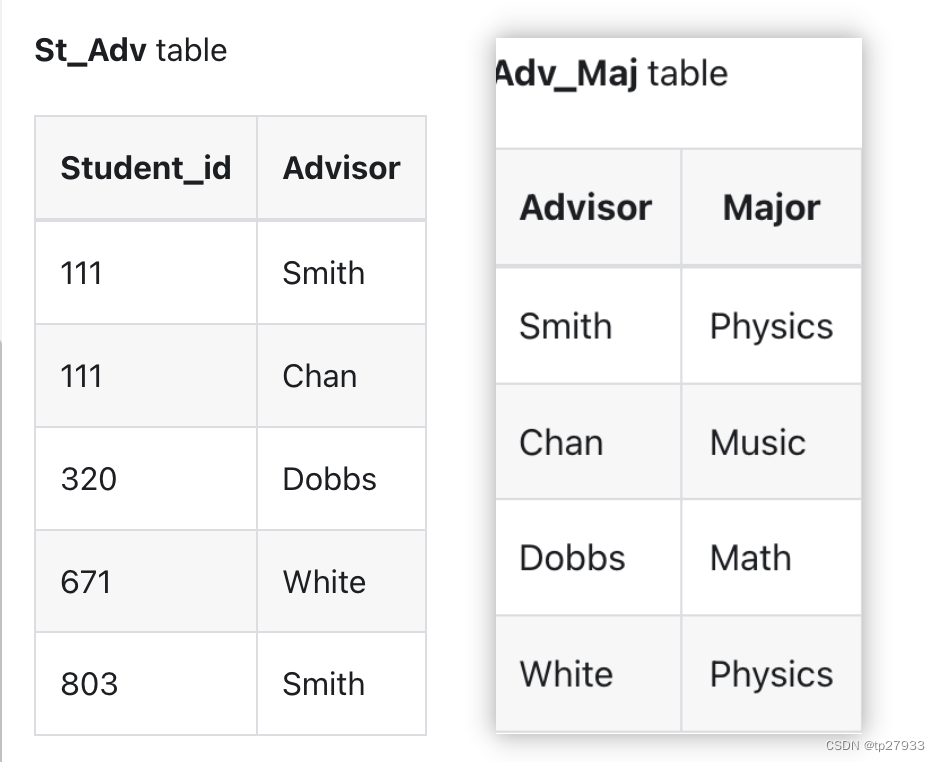
結論

• 每個階段的正規化，都會產生一個要解決的問題
  • 1NF:去除重複資料。
  • 2NF:去除部分功能相依。
  • 3NF:去除遞移相依。
  • BCNF:去除因功能相依產生的異常。
• 實務上我們都會做到第三正規化（3NF）。
• 設計不當的資料（未正規化），會導致異動操作可能會有問題。
  • 新增異常
  • 刪除異常
  • 更新異常
• 適當的正規化，可以確保數據資料的一致性。
• 當遇到資料處理速度上的困擾，或是因分割後造成的損失時，會將資料表「反正規化」。
  • 商品的庫存
  • 剩餘點數
• 在效能的考量之下的反正規化設計，需要小心控制「資料重複性的問題」及「更新的異常」。