微积分 - 导数

1、导数的定义

导数，也为叫导函数值。又名微商，是微积分中的重要基础概念，导数可以理解为自变量的变化趋势，下面用一个图去展示：

当 y = f ( x ) 的自变量 x 在一点 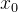$x_{0}$ 上产生一个增量 Δ x 时，函数输出值的增量 Δ y与自变量增量 Δ x 的比值在 Δ x 趋于 0 的极限 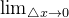$\lim_{\triangle x \to 0 }$ 如果存在，那么有：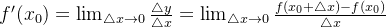

$f'(x_{0}) = \lim_{\triangle x \to 0 } \frac{\triangle y}{\triangle x} = \lim_{\triangle x \to 0 }\frac{f(x_{0}+\triangle x) - f(x_{0})}{\triangle x}$

2、左右导数

左导数：函数 f ( x ) 在某点 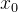$x_{0}$ 的某一左半领域 ( 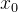$x_{0}$ − Δ x , 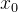$x_{0}$ ) 内有定义，当 Δ x 从左侧无限趋近于 0 时

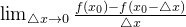$\lim_{\triangle x \to 0} \frac{f(x_{0}) - f(x_{0}-\triangle x)}{\triangle x}$ 的左极限存在，那么就称 f ( x ) 在 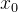$x_{0}$ 点有左导数，该极限值就是左导数的值

右导数：函数 f ( x ) 在某点 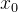$x_{0}$ 的某一右半领域 ( 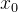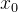$x_{0}$ ， $x_{0}$ + Δ x ) 内有定义，当 Δ x 从右侧无限趋近于 0 时

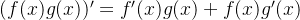$\lim_{\triangle x \to 0} \frac{f(x_{0}+\triangle x) - f(x_{0}) }{\triangle x}$ 的右极限存在，那么就称 f ( x ) 在 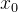$x_{0}$ 点有右导数，该极限值就是右导数的值

下面的绝对值函数的左导数和右导数不相同，左导数是 − 1 ，右导数是 + 1 ，0 位置不可导 f ( x ) = ∣ x ∣

3、可导函数

函数可导的条件如下：

函数在该点的去心邻域内有定义。
函数在该点处的左、右导数都存在。
左导数＝右导数

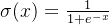
$\sigma (x) = \frac{1}{1+e^{-x}}$

4、函数求导公式

原函数	导函数
f(x)= C，C 是常数	f '(x) = 0
f(x)= 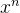$x^{n}$ ，n 是常数且n ≠ 0	f '(x) = 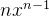$nx^{n-1}$
f(x)= lnx	f '(x) = 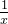$\fr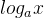ac{1}{x}$
f(x)= $log_{a}x$ a > 0且 a ≠ 1	f '(x) = 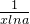$\frac{1}{xlna}$
f(x)= $e^{x}$	f '(x) = $e^{x}$
f(x)= $a^{x}$	f '(x) = $a^{x}lna$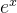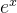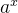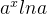
f(x)= sinx	f '(x) = cosx
f(x)=cosx	f '(x) = -sinx

5、导数的四则运算

导数加减： $(f(x) \pm g(x))' = f'(x) \pm g'(x)$

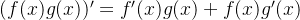
导数乘法： (f(x)g(x))' = f'(x)g(x) + f(x)g'(x)

导数除法： $(\frac{f(x)}{g(x)})' = \frac{f'(x)g(x)-f(x)g'(x)}{g^{2}(x)}$

6、复合函数求导法则

其求导有链式法则：

$\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}$

画出关系图：y → u → x ，可见从 y 到 x 有一条路径，每一段路径（对应一个导数）相乘起来。
这个规则推广到多元复合函数也是适用的：

(f(g(x)))' = f'(g(x))g'(x)

7、泰勒级数

若函数 f ( x ) 在包含 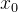$x_{0}$ 的某个开区间 ( a , b ) 上具有 ( n + 1 ) 阶导数，那么对于任意 x ∈ ( a , b ) 有：

$f(x) \approx f(x_{0}) + \frac{f'(x_{0})}{1!}f(x-x_{0})+ \frac{f''(x_{0})}{2!}f(x-x_{0})^{2}+\cdots + \frac{f^{n+1})(x_{0})}{(n+1)!}f(x-x_{0})^{n+1}$

相关阅读:
一文读懂什么是布隆过滤器
 PMP每日一练 | 考试不迷路-8.15（包含敏捷+多选）
Python爬虫如何设置代理服务器（搭建代理服务器教程）
嵌入式系统设计师考试笔记之操作系统基础复习笔记一
 EE trade：炒伦敦金的注意事项及交易指南
 计算机毕业设计高校课程评价系统的设计与实现 Java实战项目附源码+文档+视频讲解
 java飞机航班信息查询系统演示视频2021计算机毕业设计MyBatis+系统+LW文档+源码+调试部署
 Python趣味入门10:推倒繁琐化烦为简的推导式
 jsp+ssm二手车交易管理系统毕业设计-附源码151159
JAVA架构——Redis
原文地址：https://blog.csdn.net/gghhb12/article/details/133516562