代码随想录算法训练营第五十五天 | 动态规划 part 12 | 300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组

300.最长递增子序列

Leetcode

思路

1. dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
2. 递推公式：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1)
3. 初始化：每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1.
4. 顺序：从前往后

代码

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        dp = [1 for _ in range(len(nums))]
        res = 0
        for i in range(len(nums)):
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
            res = max(res, dp[i])

        return res
1
2
3
4
5
6
7
8
9
10
11

• 时间复杂度: O(n^2)
• 空间复杂度: O(n)

674. 最长连续递增序列

Leetcode

思路

本题和上题类似，区别在于连续，所以在遍历的时候只需要比较nums[i]和nums[i-1]即可。

递推公式为 if (nums[i] > nums[i - 1]) dp[i] = max(dp[i], dp[i - 1] + 1)

贪心
这道题目也可以用贪心来做，也就是遇到nums[i] > nums[i - 1]的情况，count就++，否则count为1，记录count的最大值就可以了。

代码

class Solution:
    def findLengthOfLCIS(self, nums: List[int]) -> int:
        dp = [1 for _ in range(len(nums))]
        res = 1
        for i in range(1, len(nums)):
            if nums[i] > nums[i - 1]:
                dp[i] = max(dp[i], dp[i - 1] + 1)
            
            res = max(res, dp[i])

        return res
1
2
3
4
5
6
7
8
9
10
11

• 时间复杂度: O(n)
• 空间复杂度: O(n)

718. 最长重复子数组

Leetcode

思路

寻找两个数组中最长的 公共 连续子序列。

1. dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 ）
2. 递推公式：根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1
3. 初始化：dp[i][0] 和dp[0][j]要初始值，因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1， 所以dp[i][0] 和dp[0][j]初始化为0。
4. 顺序：从前往后
5. 举例推导：A: [1,2,3,2,1]，B: [3,2,1,4,7]为例：
   

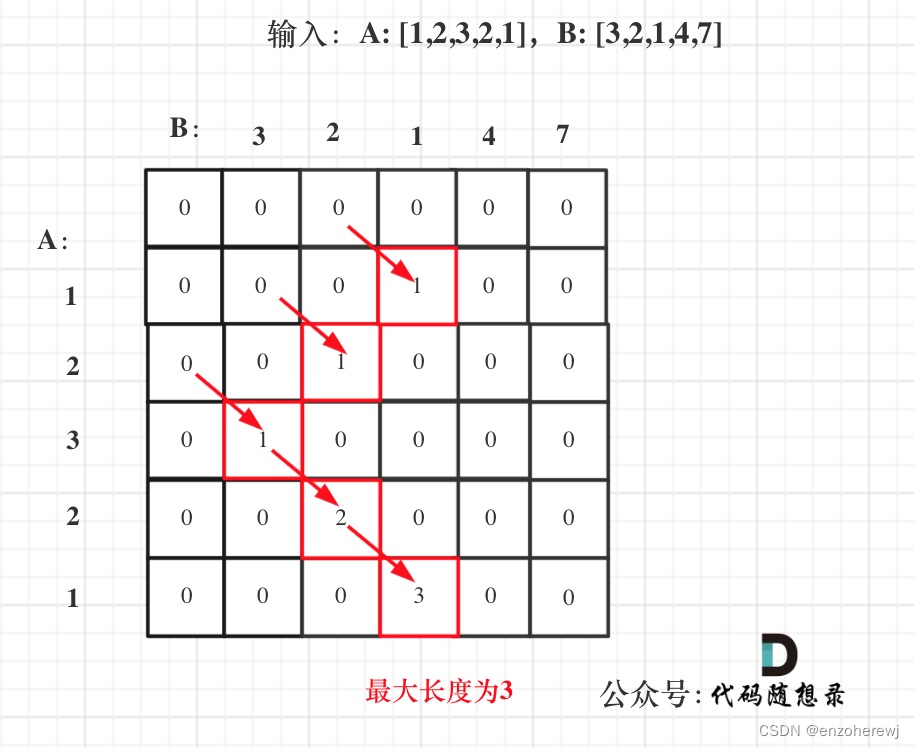
代码

class Solution:
    def findLength(self, nums1: List[int], nums2: List[int]) -> int:
        dp = [[0] * (1 + len(nums1)) for _ in range(len(nums2) + 1)]
        res = 0
        for i in range(1, len(nums2) + 1):
            for j in range(1, len(nums1) + 1):
                if nums2[i - 1] == nums1[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                res = max(res, dp[i][j])

        return res
1
2
3
4
5
6
7
8
9
10
11

• 时间复杂度: O(n × m)，n 为A长度，m为B长度
• 空间复杂度: O(n × m)