Acwing 906. 区间分组

知识点

1. 贪心

题目描述

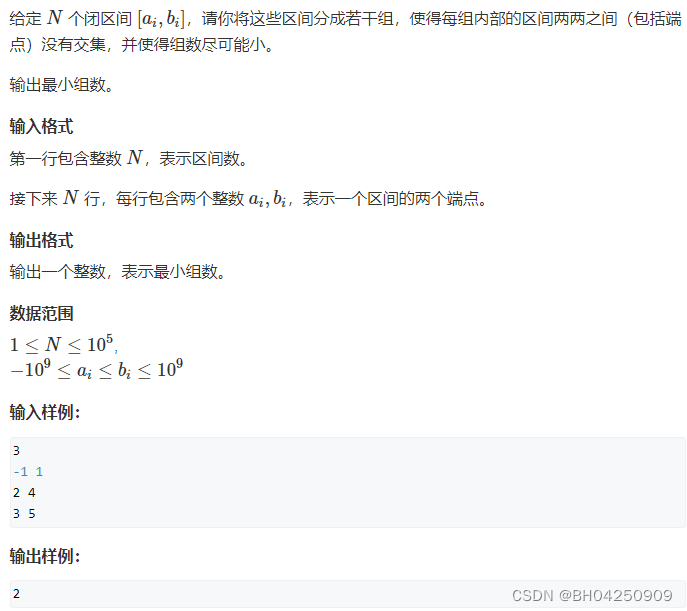
思路讲解

这段代码是用来维护一个最小堆，以确保右边界不相交的区间被正确地保留在堆中。让我详细解释这段代码：

1. heap.empty()：这个条件检查最小堆 heap 是否为空。如果堆为空，表示还没有存储任何右边界，那么当前区间 r 的右边界 r.r 就会被直接添加到堆中。

2. heap.top() >= r.l：这个条件检查当前堆中的最小右边界是否大于等于当前区间的左边界 r.l。如果最小右边界大于等于左边界，表示当前区间与之前的区间有重叠或相交，所以将当前区间的右边界 r.r 也加入堆中。

3. 如果上述两个条件都不满足，那么说明当前区间 r 的左边界 r.l 大于堆中的最小右边界，这意味着当前区间与之前的区间不相交。在这种情况下，我们可以将堆顶元素（最小右边界）弹出，然后将当前区间的右边界 r.r 添加到堆中。这样做的目的是保持堆中的右边界尽量小，以便后续区间能够更容易地与之前的区间不相交。

总之，这段代码的作用是维护一个最小堆，根据区间的左右边界来判断是否需要添加新的右边界到堆中，以确保区间不相交的右边界被正确保留在堆中，从而计算最少不相交子区间的数量。这是一个贪心算法的核心部分。

代码展示

#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n;

struct Range {
    int l, r;

    bool operator<(const Range &W) const {
        return l < W.l;
    }
} range[N];

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }

    sort(range, range + n);

    priority_queue<int, vector<int>, greater<int>> heap; // 最小堆用来存储右边界，堆顶是最小的
    for (int i = 0; i < n; i++) {
        auto r = range[i];
        if (heap.empty() || heap.top() >= r.l) heap.push(r.r);
        else {
            heap.pop();
            heap.push(r.r);
        }
    }

    printf("%d\n", heap.size());

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43