基于强化学习的节能路由（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及文章

---

💥1 概述

无线传感器设备是物联网（IoT）的支柱，使现实世界的物体和人类能够连接到互联网并相互交互，以改善公民的生活条件。然而，物联网设备受到内存和功率限制，不允许高计算应用，而路由任务是使对象成为物联网网络的一部分的原因，尽管这是一项高功耗的任务。因此，在为物联网无线网络设计路由协议时，能源效率是一个需要考虑的关键因素。在本文中，我们提出了EER-RL，一种基于强化学习的节能路由协议。强化学习 （RL） 允许设备适应网络变化，例如移动性和能量水平，并改进路由决策。将所提协议的性能与其他现有节能路由协议进行了对比，结果表明，所提协议在能效、网络寿命和可扩展性方面表现更好。

无线技术和信息系统以及移动技术的出现为物联网（IoT）开辟了一个新时代。后者已成为无处不在的计算的支柱，同时通过识别、识别对象、数据生成、传输和检索使环境变得智能[1,2].物联网允许现实世界的事物和人通过无线通信连接并成为互联网虚拟世界的一部分。最初，物联网一直针对RFID标签网络，后来它已广泛扩展到各种设备和应用，目标是首先使对象能够学习和理解其环境并与之交互[3].通过无线通信，这些对象可以相互交互，并使系统能够通过互联网连接进行远程控制[2–5].由于其对各个领域的影响，物联网最近受到广泛关注，并已广泛应用于智慧城市、智能医疗系统、智能家居、对象跟踪、灾害管理和环境监测等广泛应用 [6,7].

物联网由异构无线设备的互连组成，包括智能手机、无线传感器、执行器、射频 （RFID） 标签识别以及具有传感功能的真实世界事物 [8,9].通常，传感器设备包括四个单元，即功率单元、传感单元、处理单元和通信单元[10–13].传感单元负责从周围环境中感知数据，而处理单元执行计算任务。通信单元负责通过网络发送数据包。最后，动力单元由一个小电池组成，为其余三个模块供电。从逻辑上讲，动力单元不消耗任何能量，而是向其他模块提供能量，传感模块和处理模块也消耗的能量可以忽略不计，而通信模块是最耗能的[14–16].

但是，为了在物联网中容纳大量设备，需要几个要求，包括能源效率、可扩展性、互操作性、安全性和灵活性 [2].能源效率对于在尽可能长时间内保持全面运营的网络至关重要 [16,17]，特别是对于部署在无法充电和更换电池的恶劣环境中的设备。因此，众所周知，节能路由协议可以管理设备可用能量的消耗并延长网络的使用寿命[6,13].

强化学习是机器学习的一个子领域，它解决了代理在未知环境中采取行动的问题，并通过与环境的一系列试错交互随着时间的推移而改进[18].换句话说，代理通过执行操作与环境交互并获得奖励，当执行的操作正确时，奖励可以是积极的，否则可以是消极的。与静态路由方法相比，这种方法带来了数据路由的动态性和网络通信的适应能力[19–21].在物联网网络中，RL可用于处理由于设备的移动性，能量水平和其他传输参数（例如距离，信号强度和带宽）而导致的网络拓扑变化等问题，这些问题可能会随时间变化并影响网络性能。

在本文中，我们提出了EER-RL，一种基于强化学习的物联网节能路由协议。所提出的EER-RL平衡了物联网网络中设备之间的能量耗散，延长了网络寿命，提高了网络的可扩展性。EER-RL还使用反馈机制提供最佳路径，以共享本地信息作为奖励，后者使用剩余能量和跳到接收器的跳数计算，并且跳数参数可以减少端到端延迟。为了评估EER-RL的性能，我们进行了仿真，结果表明EER-RL实现了高效的能耗，延长了网络寿命，并且对于大规模物联网网络更具可扩展性。EER-RL也与利奇[22]和飞马[23]，比较结果表明，EER-RL通过提供更好的能量平衡和延长网络寿命而优于它们。

本文的其余部分组织如下：在部分2，我们概述了RL及其在路由中的应用。部分3讨论使用 RL 的路由协议的现有解决方案。部分4描述了我们提出的解决方案。建议的解决方案的性能评估在一节中介绍5，然后是结论意见和本节的未来工作6.

RL 问题被形式化为带有元组 （S， A， P， R） 的马尔可夫决策过程 （MDP），其中 S 表示代理在给定时间 t 可以处于的一组状态;A 是代理可以采取的一组可能的操作。代理在给定时间 t 和从给定状态 s（t） 执行动作 a（t） 进入状态 s（t + 1） 的转移概率表示为 P，R 是代理因执行的操作而获得的奖励 [18].将 RL 应用于路由协议需要定义 RL 模型的主要组件，例如代理和环境、状态和操作以及奖励。首先，代理是RL模型的决策者，而环境是代理观察并对其做出反应的内容。在物联网网络中，每个设备都被视为代理;对于整个网络，需要多代理 RL。其次，状态是关于给定时间环境的任何有用信息，而动作是代理在给定状态下的反应。代理的状态空间是来自所有可用相邻设备的可用路由信息。状态可以是决策因素的元组，例如剩余能量、跃点数和信号强度，具体取决于设计协议时考虑的因素。另一方面，操作是指选择下一跳将数据包路由到基站。因此，操作空间表示在给定时间通过邻居的所有可用路由的集合。第三，代理在给定状态下执行的操作的成本称为奖励。

在实现拟议协议时考虑了以下定义：（1）网络中的每个设备都被视为代理，（2）对于每个设备，通过其相邻设备到基站的可用路由集是状态空间。（3） 数据包可以通过其发送到基站的所有可用邻居的集合表示为操作空间。（4）代理人的行为被表示为政策。

策略映射状态-操作对;它可以是随机的或确定性的，并随着时间的推移而改善。每个 RL 模型的目标都是找到一个最佳策略，以最大化每个状态-操作对的长期奖励 [18,19];可以使用策略迭代过程实现此目标，该过程包括评估和改进给定的策略。政策评估从结果评估政策，而政策改进则使政策朝着最佳政策改进[18,20].数字1描述了一个简单的 RL 模型。

详细讲解见第4部分。

📚2 运行结果

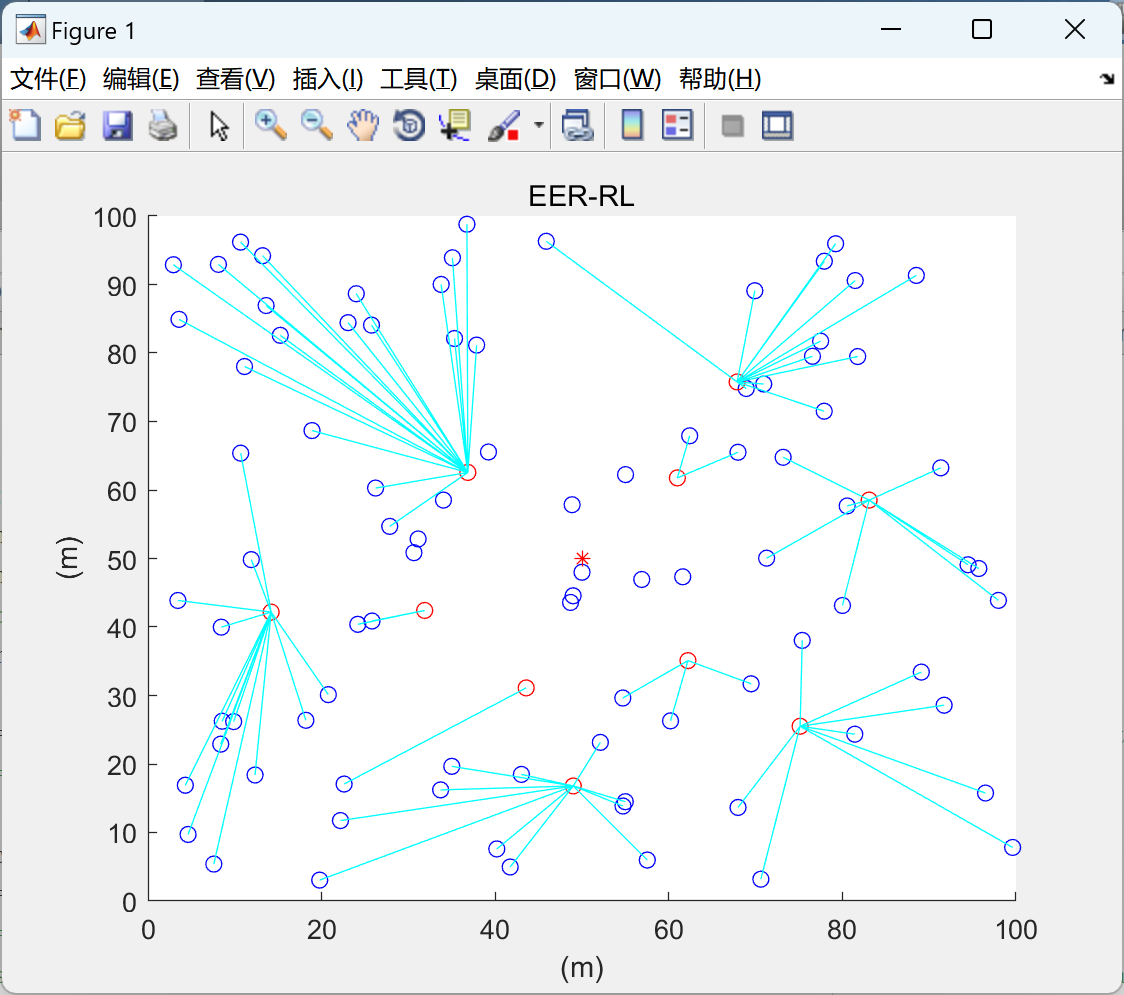
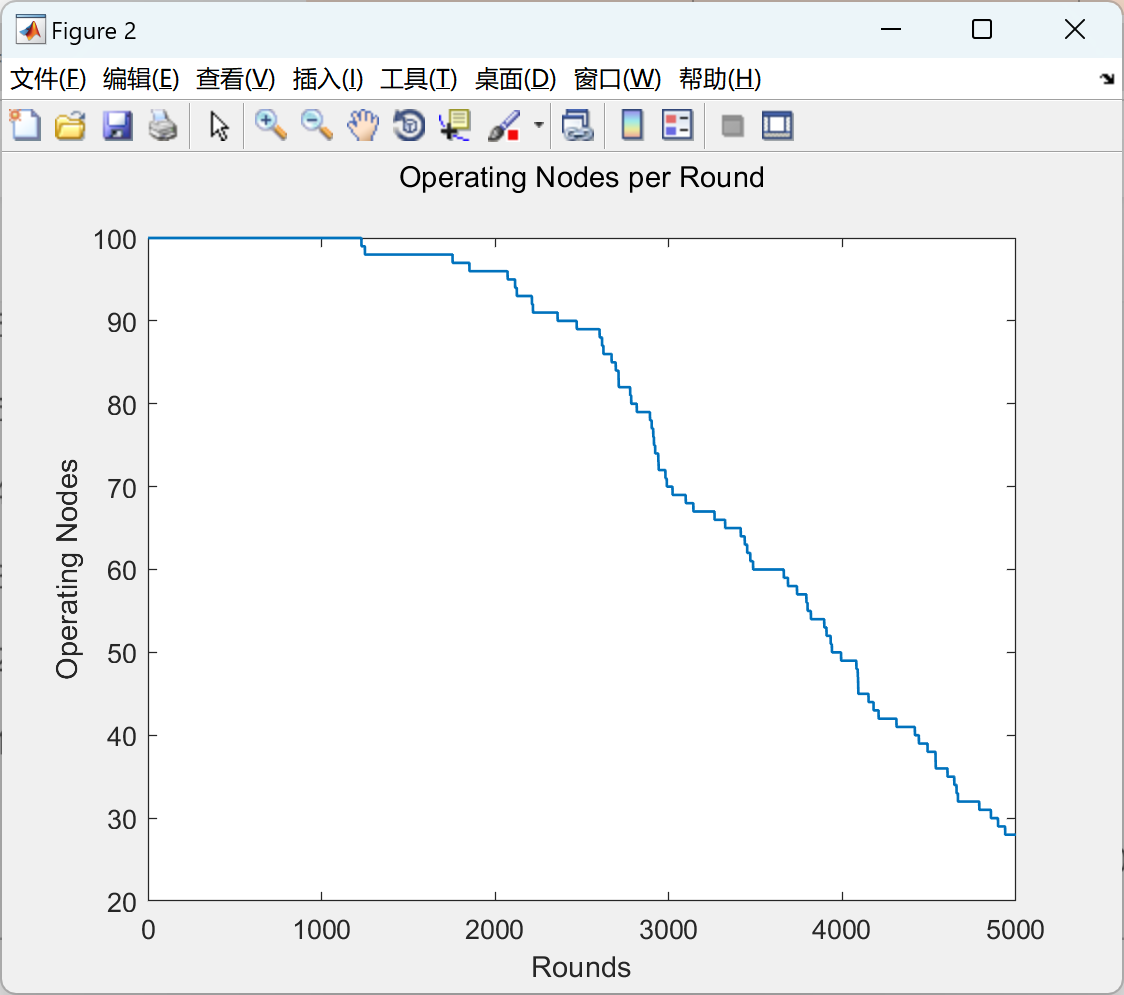
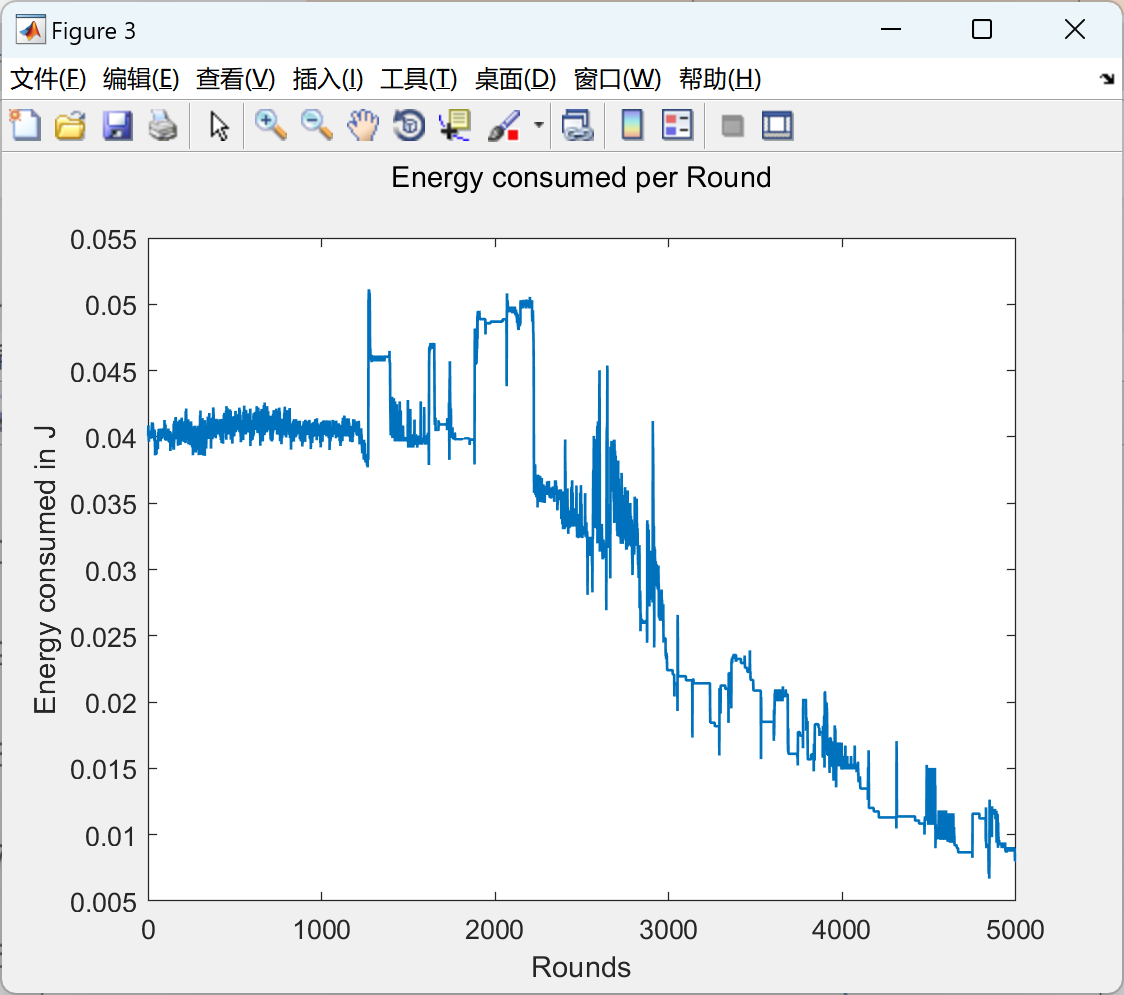
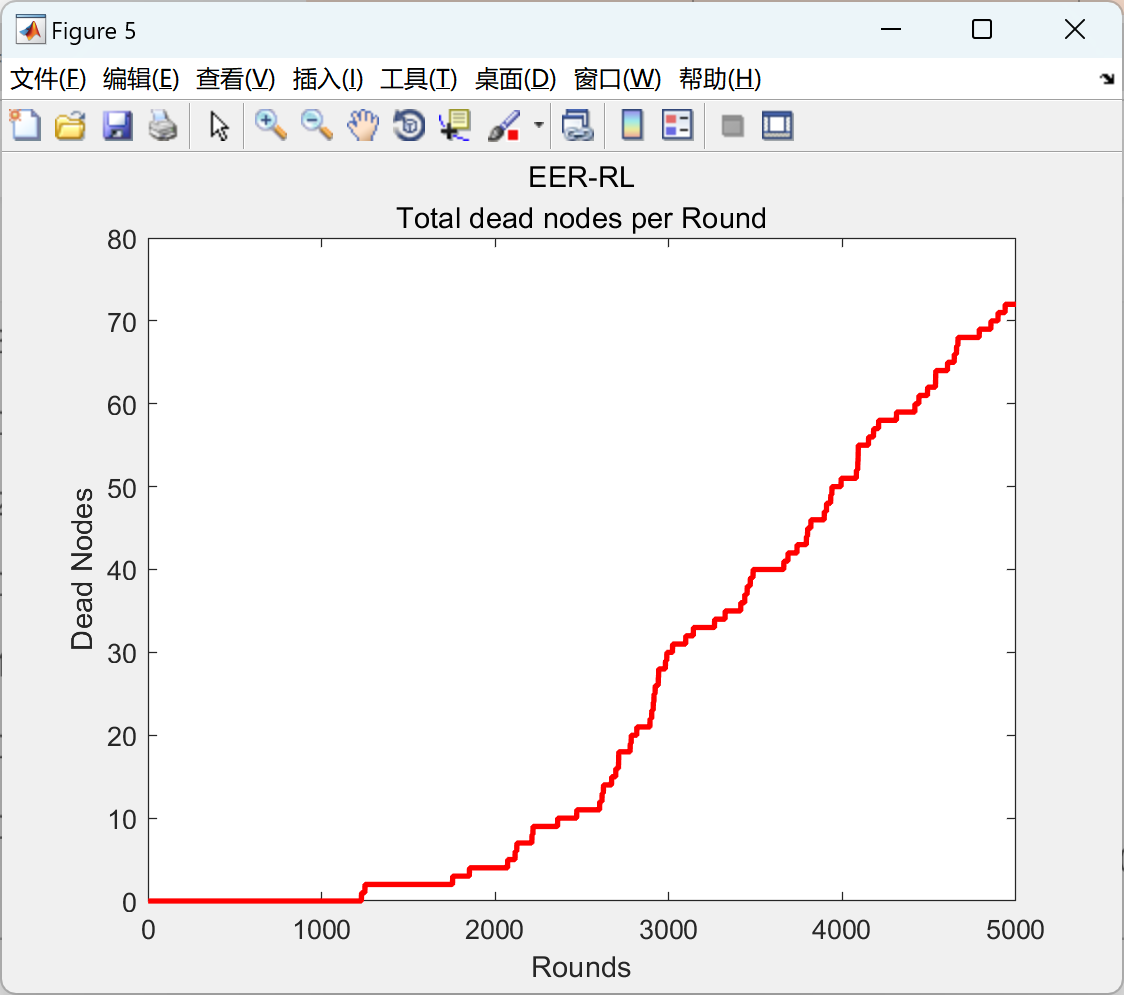
部分代码：

%%% Energy parameters %%%
Eo=2; % Initial Energy of nodes (in Joules)
% Energy required to run circuity (both for transmitter and receiver) %
Eelec=50*10^(-9); % units in Joules/bit
ETx=50*10^(-9); % units in Joules/bit
ERx=50*10^(-9); % units in Joules/bit
% Transmit Amplifier Types %
Eamp=100*10^(-12); % units in Joules/bit/m^2 (amount of energy spent by the amplifier to transmit the bits)
% Data Aggregation Energy %
EDA=5*10^(-9); % units in Joules/bit
% Size of data package %
k=4000; % units in bits 
% Round of Operation %
rnd=0;
tot_rnd=10000;
% Current Number of operating Nodes %
op_nodes=n; %Operating nodes
transmissions=0;
d(n,n)=0;
source=1;
flag1stdead=0;
range_C = 20; %Communication range
alpha=1; %Learning Rate
gamma = 0.8; % Discount Factor
p=0.7 % Energy's Probabilistic parameter
q1=0.3 % Hop count probabilistic parameter
%%%%%%%%%%%%%%%%%%%%%%%%%%% End of Network settings %%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%% WSN Creattiom %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Plotting the WSN %
for i=1:n
    
    
    NET(i).id=i;	% sensor's ID number
    NET(i).x=rand(1,1)*xm;	% X-axis coordinates of sensor node
    NET(i).y=rand(1,1)*ym;	% Y-axis coordinates of sensor node
    NET(i).E=Eo;     % nodes energy levels (initially set to be equal to "Eo"
    %NET(i).E = randi([2,6]); % For heterogeneous WNET
    NET(i).cond=1;   % States the current condition of the node. when the node is operational its value is =1 and when dead =0
    %NET(i).dts=0;    % nodes distance from the sink
    NET(i).dts= sqrt((sinkx-NET(i).x)^2 + (sinky-NET(i).y)^2);
    NET(i).hop=ceil(NET(i).dts/range_C); %Hop count estimate to the sink
    %NET(i).role=0;   % node acts as normal if the value is '0', if elected as a cluster head it  gets the value '1' (initially all nodes are normal)
    %NET(i).pos=0;
    %NET(i).first=0;  %Initial route available. If it the first time a node send a packet its value is 0, otherwise it's 1
    NET(i).closest=0;
    NET(i).prev=0;
    %NET(i).next=0;
    %NET(i).dis=0;	% distance between two nodes headin towards to the cluster head from position 1
    NET(i).sel=0;    % states if the node has already operated for this round or not (if 0 then no, if 1 then yes) 
    NET(i).rop=0;    % number of rounds node was operational
    %NET(i).tel=0;    % states how many times the node was elected as a Cluster Head
    %order(i)=0;
    hold on;
    figure(1);
    plot(x,y,xm,ym,NET(i).x,NET(i).y,'ob',sinkx,sinky,'*r');
    
    title 'RL-EBRP';
    xlabel '(m)';
    ylabel '(m)';
end
% find Neighbord nodes
%Compute Q-Value
min_E = min([NET.E]); 
max_E = max([NET.E]);
for i=1:n
    if(min_E ==max_E)
        Q(i) = 1 / NET(i).hop;
        NET(i).Q = Q(i);
    else
        Q(i) = (p*(NET(i).E - min_E)/(max_E-min_E)+(q1/NET(i).hop));
        NET(i).Q = Q(i);
        %CH = maxk(Q,10); %Find 10 strongest nodes 
    end

%%% Energy parameters %%%
Eo=2; % Initial Energy of nodes (in Joules)
% Energy required to run circuity (both for transmitter and receiver) %
Eelec=50*10^(-9); % units in Joules/bit
ETx=50*10^(-9); % units in Joules/bit
ERx=50*10^(-9); % units in Joules/bit
% Transmit Amplifier Types %
Eamp=100*10^(-12); % units in Joules/bit/m^2 (amount of energy spent by the amplifier to transmit the bits)
% Data Aggregation Energy %
EDA=5*10^(-9); % units in Joules/bit
% Size of data package %
k=4000; % units in bits 
% Round of Operation %
rnd=0;
tot_rnd=10000;
% Current Number of operating Nodes %
op_nodes=n; %Operating nodes
transmissions=0;
d(n,n)=0;
source=1;
flag1stdead=0;
range_C = 20; %Communication range
alpha=1; %Learning Rate
gamma = 0.8; % Discount Factor
p=0.7 % Energy's Probabilistic parameter
q1=0.3 % Hop count probabilistic parameter
%%%%%%%%%%%%%%%%%%%%%%%%%%% End of Network settings %%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%% WSN Creattiom %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Plotting the WSN %
for i=1:n
    
    
    NET(i).id=i;    % sensor's ID number
    NET(i).x=rand(1,1)*xm;    % X-axis coordinates of sensor node
    NET(i).y=rand(1,1)*ym;    % Y-axis coordinates of sensor node
    NET(i).E=Eo;     % nodes energy levels (initially set to be equal to "Eo"
    %NET(i).E = randi([2,6]); % For heterogeneous WNET
    NET(i).cond=1;   % States the current condition of the node. when the node is operational its value is =1 and when dead =0
    %NET(i).dts=0;    % nodes distance from the sink
    NET(i).dts= sqrt((sinkx-NET(i).x)^2 + (sinky-NET(i).y)^2);
    NET(i).hop=ceil(NET(i).dts/range_C); %Hop count estimate to the sink
    %NET(i).role=0;   % node acts as normal if the value is '0', if elected as a cluster head it  gets the value '1' (initially all nodes are normal)
    %NET(i).pos=0;
    %NET(i).first=0;  %Initial route available. If it the first time a node send a packet its value is 0, otherwise it's 1
    NET(i).closest=0;
    NET(i).prev=0;
    %NET(i).next=0;
    %NET(i).dis=0;    % distance between two nodes headin towards to the cluster head from position 1
    NET(i).sel=0;    % states if the node has already operated for this round or not (if 0 then no, if 1 then yes) 
    NET(i).rop=0;    % number of rounds node was operational
    %NET(i).tel=0;    % states how many times the node was elected as a Cluster Head
    %order(i)=0;

    hold on;
    figure(1);
    plot(x,y,xm,ym,NET(i).x,NET(i).y,'ob',sinkx,sinky,'*r');
    
    title 'RL-EBRP';
    xlabel '(m)';
    ylabel '(m)';
end

% find Neighbord nodes
%Compute Q-Value
min_E = min([NET.E]); 
max_E = max([NET.E]);
for i=1:n
    if(min_E ==max_E)
        Q(i) = 1 / NET(i).hop;
        NET(i).Q = Q(i);
    else
        Q(i) = (p*(NET(i).E - min_E)/(max_E-min_E)+(q1/NET(i).hop));
        NET(i).Q = Q(i);
        %CH = maxk(Q,10); %Find 10 strongest nodes 
    end

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码及文章