简单讲解 glm::mat4

---

前言

glm库是OpenGL的官方数学库，里面内置多种跟几何变换相关的函数，熟练掌握glm库可以省下很多麻烦。
因为最近在项目中主要使用了 glm::mat4 ，所以加上我自己的理解，想分享一下。

---

一、下载glm库

我下载的是：glm 0.9.9.8 版本。

二、基本数学知识

1. 三维中的 4 x 4 矩阵

在三维计算中，使用一个 4 x 4 的齐次矩阵可以表示旋转、位移和缩放。这个 4 x 4 的矩阵就是对应glm::mat4类型。注意：glm::mat4 是float类型。
具体的分析过程可以看：LearnOpenGL CN - 入门-变换 这一节的内容。下面是一些结论。

2.旋转

3. 位移

4. 缩放

5. 组合

---

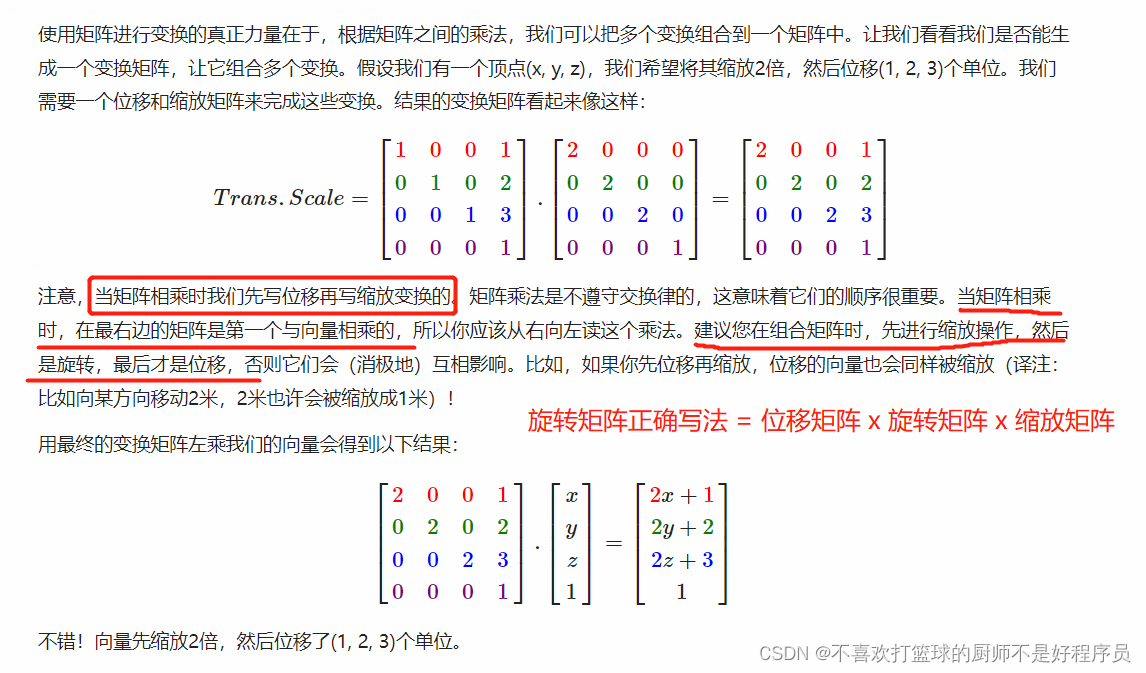
三、行向量或列向量

无论是上面的分析，还是现实生活中的数学计算，基本都是以行向量为主。但是，我们要知道，计算机本身的存储并没有方向之分，是我们自己的读取或者写入逻辑赋予了它顺序。
glm库在创建之时，为了兼容其他的东西（具体我忘了），导致它是以列向量的方向进行存储。这就与我们的常识相反。所以，就需要一些特殊的技巧，来避免转换错误。
具体看下面的代码：

#include 
#include 

int main()
{
#pragma region 1. 准备一个 4 * 4 的行向量矩阵
    /*
    *  1.0, 0.0, 0.0, 10.0
    *  0.0, 1.0, 0.0, 20.0
    *  0.0, 0.0, 1.0, 30.0
    *  0.0, 0.0, 0.0, 1.0
    */
    float mat0[4][4] = {
        {1.0f, 0.0f, 0.0f, 10.0f},
        {0.0f, 1.0f, 0.0f, 20.0f},
        {0.0f, 0.0f, 1.0f, 30.0f},
        {0.0f, 0.0f, 0.0f, 1.0f}
    };
#pragma endregion

#pragma region 2. 将 unit_mat 转换为 glm::mat4 类型
    glm::mat4 mat1{ 0.0f };
    for (int r = 0; r < 4; ++r)
    {
        for (int c = 0; c < 4; ++c)
        {
            mat1[r][c] = mat0[c][r];
        }
    }

    for (int r = 0; r < 4; ++r)
    {
        for (int c = 0; c < 4; ++c)
        {
            std::cout << mat1[c][r] << " ";      // 列向量，所以第一个[]代表的是列，第二个[]代表的是行
        }
        std::cout << std::endl;
    }
    /* 输出
    * 1 0 0 10
    * 0 1 0 20
    * 0 0 1 30
    * 0 0 0 1
    */
#pragma endregion

#pragma region 3. 将 glm::mat4 转回 列向量 的 float[4][4]
    float mat2[4][4]{ 0.0f };
    for (int r = 0; r < 4; ++r)
    {
        for (int c = 0; c < 4; ++c)
        {
            mat2[r][c] = mat1[r][c];
        }
    }

    for (int r = 0; r < 4; ++r)
    {
        for (int c = 0; c < 4; ++c)
        {
            std::cout << mat2[c][r] << " ";      
        }
        std::cout << std::endl;
    }
    /* 输出
    * 1 0 0 10
    * 0 1 0 20
    * 0 0 1 30
    * 0 0 0 1
    */
#pragma endregion
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

---

四、总结

总而言之，无论是使用 glm::mat4，还是float[4][4]，还是float[16]，你都要先想用行向量表示出来你的矩阵，然后再去转换，这样就一定没错！