• [PyTorch][chapter 55][WGAN]

    前言：

             前面讲到GAN 在训练生成器的时候，如果当前的Pr 和 Pg 的分布不重叠场景下：

    JS散度为一个固定值，梯度为0，导致无法更新生成器G

             WGAN的全称是WassersteinGAN，它提出了用Wasserstein距离（也称EM距离）去取代JS距离，这样能更好的衡量两个分布之间的divergence。

    目录：

    1.      GAN 数据分布问题
    2.      GAN JS 散度问题
    3.      EM 距离
    4.      WGAN
    5.      WGAN-GP
    6.      伪代码分析

    一  GAN 数据分布问题

           在大部分场景 :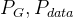P_G,P_{data} 分布不重叠

            原因1 ：数据空间的维度

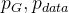
                       如下图   p_G,p_{data}

                       在低维空间是个有重叠的流形 ，

                       在高维空间展开就是不重叠的 线或者平面

                       图片可以认为是高维的空间

                 

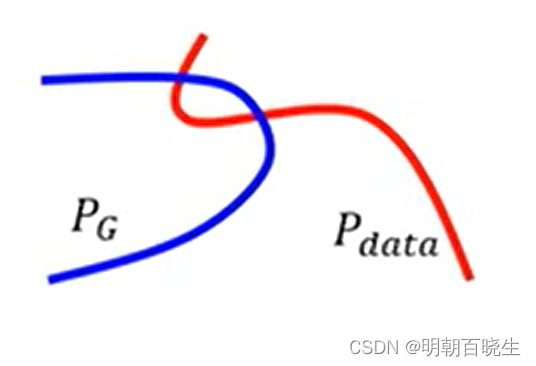
              原因2: 采样

                     我们生成器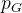p_G 和真实的数据 p_{data} 虽然有重叠

    但是实际采样的时候,生成的图片和真实图片分布

    不一定重叠，如下

        

                   

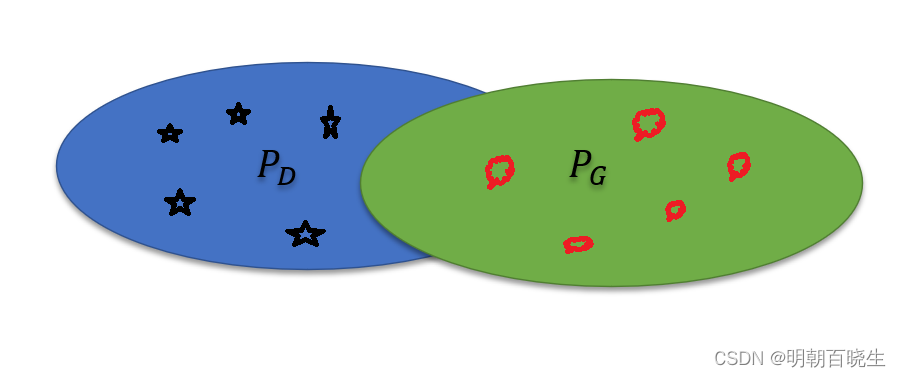
    二   GAN JS 散度问题

          2.1  JS 散度问题

                   前面讲过, 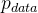p_{data} 和 生成器生成的分布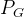 P_{G}

          不重叠的时候,JS 散度为常数 log2, 此刻梯度为0.

           导致生成器无法更新。

                  因为生成器G很弱,制作出来的数据很假,鉴别器D 很容易

            鉴别出,导致鉴别器D也无法更新。

          

               2.2    Least Square Gan

                   针对JS 散度为常数问题，梯度为0，早期提出了用linear 替代

    sigmoid 来分类，解决该问题。

    三 EM 距离

         WGAN 里面采用了EM 距离。

         3.1 简介

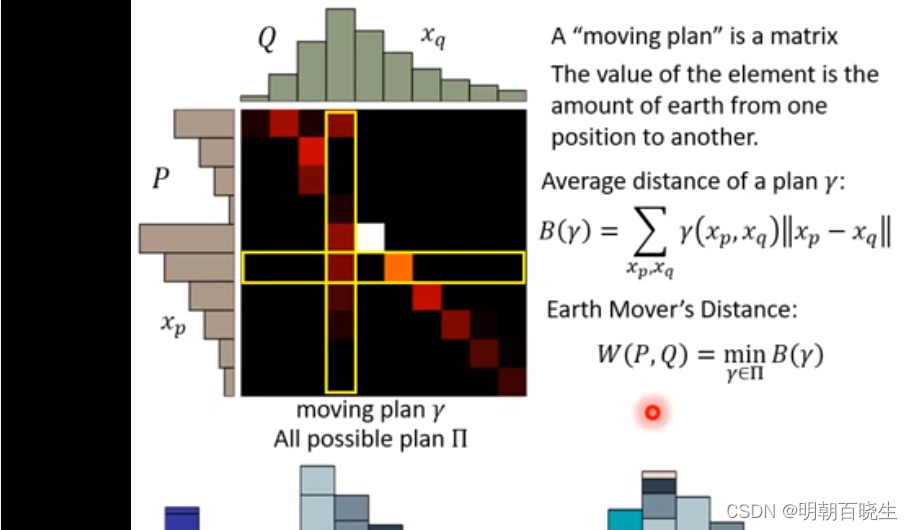
             Wasserstein 距离又叫Earth-Mover（EM）距离，又叫推土机距离。

            如下图1维空间里面两个分布，P,Q,如果把P 移动到Q,则需要d步。

                 

     

          把P 分布变成Q 分布,有不同的铲土方案.

          穷举所有的可能方案，其中铲土距离最小的，称为Wasserstein 距离。

          

         

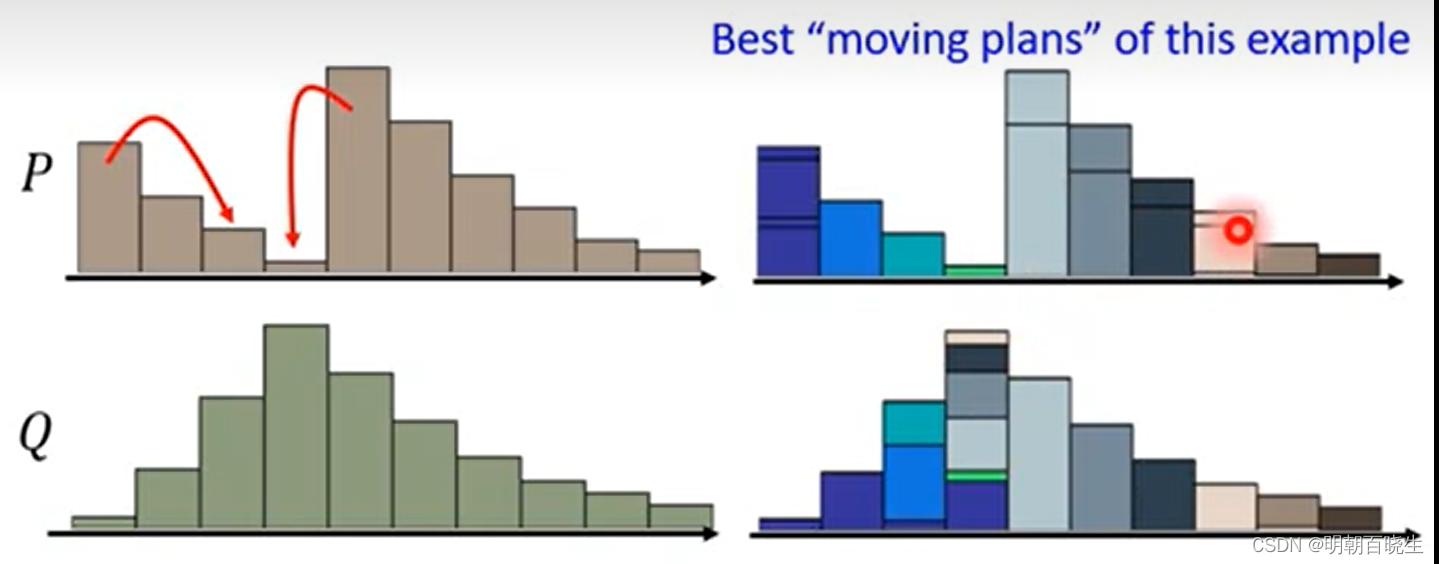
    3.2   EM 距离矩阵表示

            如下图,把分布P 移动到分布Q.

    有不同的移动的方案,每一种方案称为r.

    矩阵里面每个元素的值 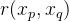r(x_p,x_q) 代表移动的土量。

    用不同颜色表示,颜色越深值越大。

      P 上每个位置的值： 等于矩阵当前行的值，

      Q 上每个位置的值 ： 等于矩阵当前列的值

            

    3.2 EM 距离的优势

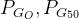
             如下图：P_{G_O},P_{G_{50}}

                       JS 散度： 都是一样 log2,无法分辨出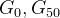G_0,G_{50} 哪个生成器更好

                       EM 距离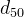： d_{50} 距离更小，通过训练，可以把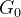G_0 训练成G_{50}

      

         。

                

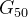
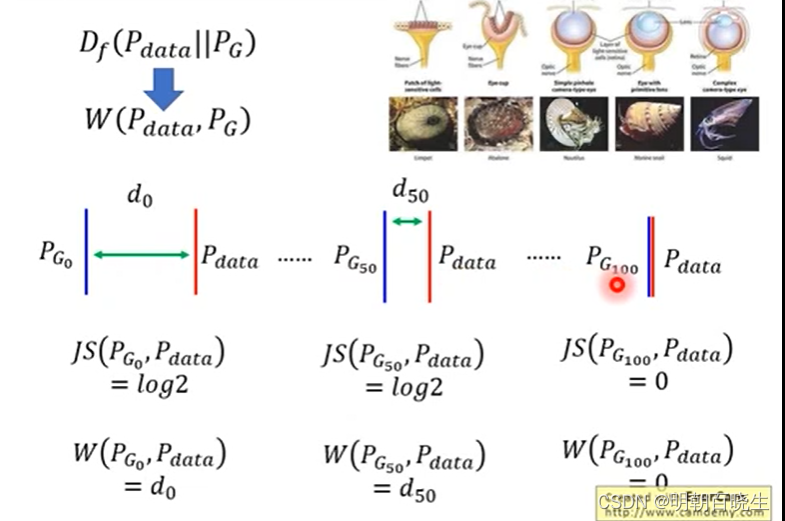           KL散度和JS散度是突变的，要么最大要么最小，Wasserstein距离却是平滑的，如果我们要用梯度下降法优化这个参数，前两者根本提供不了梯度，Wasserstein距离却可以。

           在高维空间中如果两个分布不重叠或者重叠部分可忽略，则KL和JS既反映不了远近，也提供不了梯度，但是Wasserstein却可以提供有意义的梯度。   

    四     WGAN 

        4.1  优化目标：

       GAN 里面 wassertein 距离度量方法如下：

      针对鉴别器我们期望： 

              E_{x \sim p_{data}}[D(x)] 越大越好

              E_x{x \sim p_G}[D(x)] 越小越好

        4.2 问题：

            对D(x)没有约束的时候，，会导致训练的时候，无法收敛。

             E_{x\sim p_{data}} [D(x)] \mapsto\infty

                E_{x \sim p_G} [D(x)] \mapsto -\infty

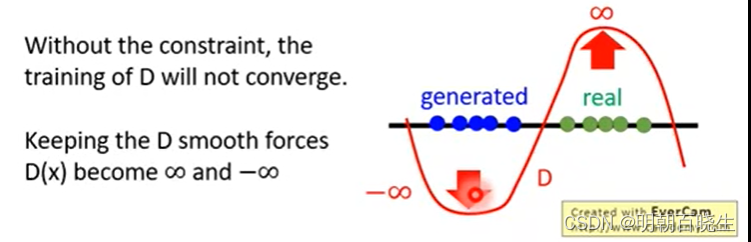
     4.3 解决方案

         加入了Lipschitz 约束，要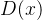D(x) 变化不是很大，在一个约束范围内，该约束条件称为

    Lipschitz。

         Lipschitz 定义

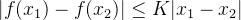
          |f(x_1)-f(x_2)|\leq K|x_1-x_2|

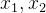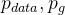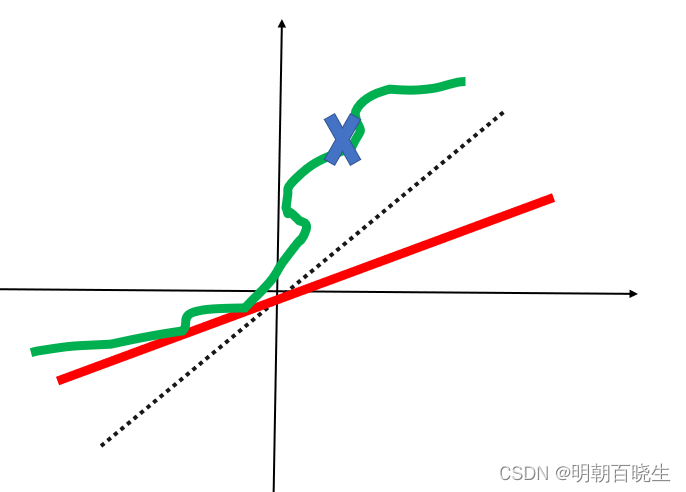
         WGAN 里面，f 相当于 D， x_1,x_2相当于p_{data},p_g sample出来的样本

         当k =1 ，称为1-Lipschitz。如下图的红线符合1-Lipschitz，

    绿线不符合 1-Lipschitz 条件

    4.4 Weight Clip

               早期解决方案：

                 当w >c, w=c

                 当 w<-c, w=-c

           约束参数的变化，但是并不能满足1-Lipschitz，只是发现实际工程效果比较好

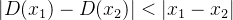
         |D(x_1)-D(x_2)|<|x_1-x_2|

    五   WGAN-GP

        前面讲过1-Lipschitz

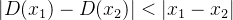
        |D(x_1)-D(x_2)|<|x_1-x_2|

        等价于在每个位置

       

         5.1 优化目标

               增加了Penalty 项

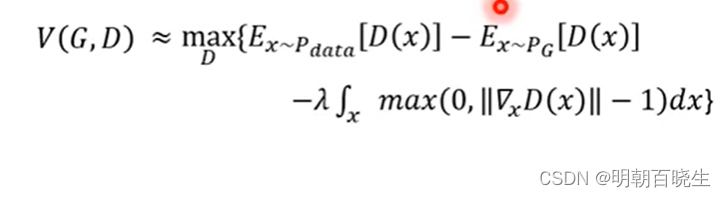
        问题

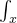        \int_x  没办法计算，所有可能的x 进行积分

        5.2  解决方案

          假设 x 是从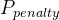P_{penalty} 里面采样出来的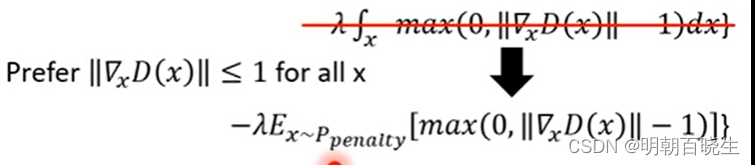

         

       5.3 penalty 采样

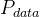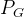            P_{data},P_{G} 两点相连接，在连接线上随机采样一个点，称为penalty中的x

           

      在每个位置强制的Lipschitz条件是不可能的，通过Penalty 机制，在蓝色的区域进行

    满足Lipschitz，实验上效果也很好

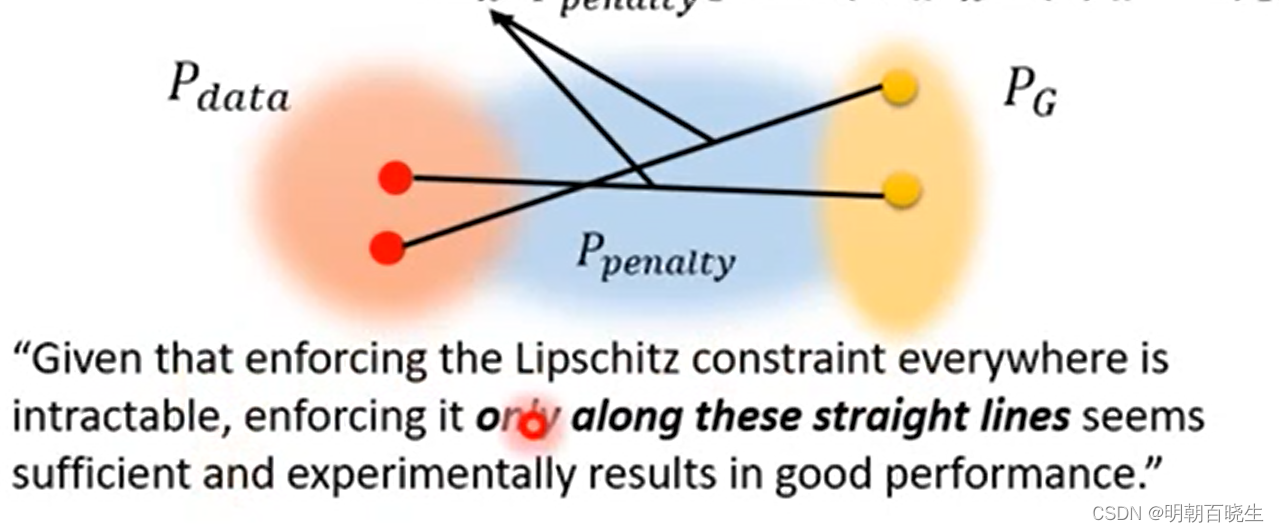
    5.4 penalty 方案2

       如下图，也可以用绿色的代表penalty,即使Norm 小于1 也进行Penalty,

    有点类似SVM 思想，强制要求在-1,1 超平面上。

      

    5.5 Spectrum Norm

              在每个地方都满足gradient <1

    六  GAN伪代码分析

         6.1 训练鉴别器D,训练K次

        

          6.2  训练生成器G

                

    七  WGAN 伪代码

        4处不一样

        7.1 训练D

      

         注意要使用Weight Clipping or Gradient Penalty

       7.2 训练G

          

    注意训练D的时候要使用Weight Clipping or Gradient Penalty

    参考：

    课时130 WGAN-GP实战_哔哩哔哩_bilibili

    什么是利普希茨条件？ - 知乎

    https://www.cnblogs.com/breadcake/p/16861792.html

    令人拍案叫绝的Wasserstein GAN - 知乎

    WGAN 李-哔哩哔哩_Bilibili

    GAN Lecture 6 (2018): WGAN, EBGAN_哔哩哔哩_bilibili

  • 相关阅读:
    中台框架模块开发实践-用 Admin.Core 代码生成器生成通用代码生成器的模块代码
    常见排序算法要点
    （黑马出品_02）SpringCloud+RabbitMQ+Docker+Redis+搜索+分布式
    【线性代数】P2 余子式与代数余子式&异乘变零定理
    MySQL 从入门到实战讲解，京东 T5 大咖学习笔记分享，看完我哭了
    CentOS 7 中安装Kafka
    Vue中实现清空数组和清空el-table
    聊聊我认为的 “Kotlinic“
    解决redis在centos上部署
    ECCV2022|时尚领域的多模态预训练预训练模型FashionViL，在五个下游任务中SOTA！
  • 原文地址：https://blog.csdn.net/chengxf2/article/details/133037783