-
机器学习---BP算法
1. 多级网络
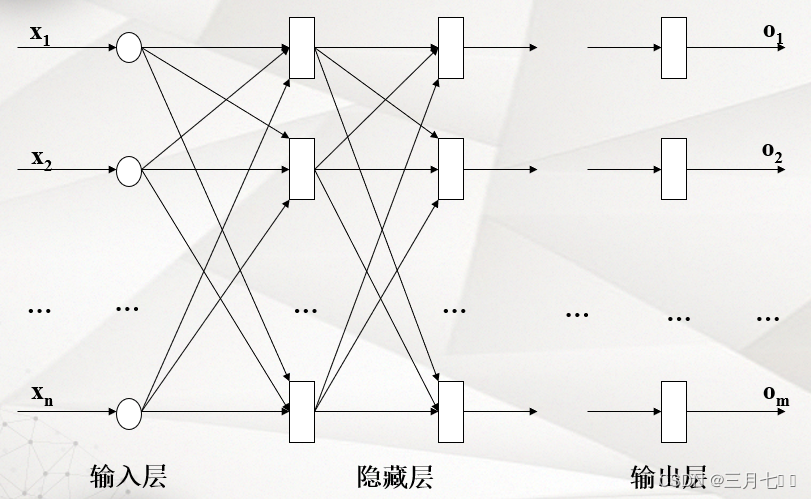
层号确定层的高低:层号较小者,层次较低,层号较大者,层次较高。
输入层:被记作第0层。该层负责接收来自网络外部的信息。
第j层:第j-1层的直接后继层(j>0),它直接接受第j-1层的输出。
输出层:它是网络的最后一层,具有该网络的最大层号,负责输出网络的计算结果。
隐藏层:除输入层和输出层以外的其它各层叫隐藏层。隐藏层不直接接受外界的信号,也不直接向
外界发送信号。
输出层的层号为该网络的层数:n层网络,或n级网络。
第j-1层到第j层的联接矩阵为第j层联接矩阵,输出层对应的矩阵叫输出层联接矩阵。
2. BP算法
BP网络主要用于:
1)函数逼近:用输入向量和相应的输出向量训练一个网络逼近一个函数。
2)模式识别:用一个特定的输出向量将它与输入向量联系起来。
3)分类:把输入向量 以所定义的合适方式进行分类。
4)数据压缩:减少输出向量维数以便于传输或存储。
基本原理:利用输出误差来估计输出层的直接前导层的误差,在用这个误差估计更前一层的误
差,如此一层一层的反传下去,就获得了所有其他各层的误差估计,利用此误差更新权重。
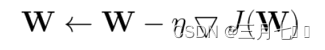
W是网络的参数,J是目标函数。
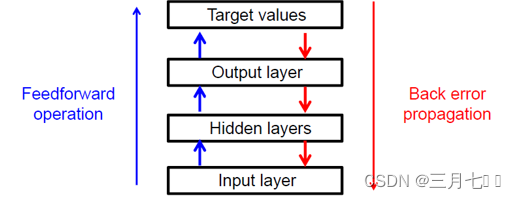
基本学习过程:神经网络在外界有导师输入样本的刺激下,不断改变网络的连接权值,以使网络的
输出不断接近期望的输出。
学习的本质:对各连接权值的动态调整。
学习规则:将误差分摊给各层的所有单元——各层单元的误差信号,修正各层连接权值。
信号前馈:输入样本-->输入层-->各隐层-->输出层。
判断是否转入反向传播阶段:若输出层的实际输出与期望输出(教师信号)不符。
误差反传:误差以在各层表达,并借此来修正各层单元的权值,网络输出的误差减少到可接受的程
度或进行到预先设定的学习次数为止。
一个隐含层(也可以看成3层BP网络):
①期望输出:
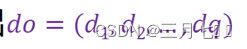
②误差函数e(第K个样本):
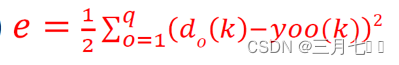
③激活函数f(.)
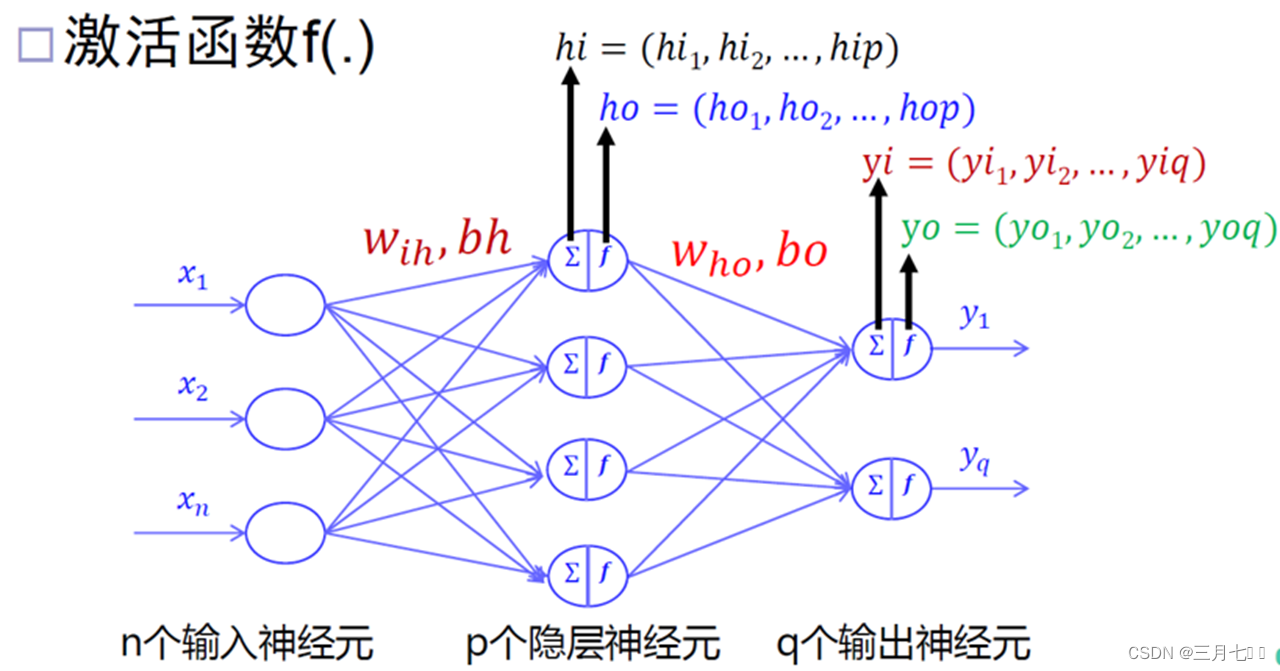
激活函数必须处处可导,比如:sigmoid函数
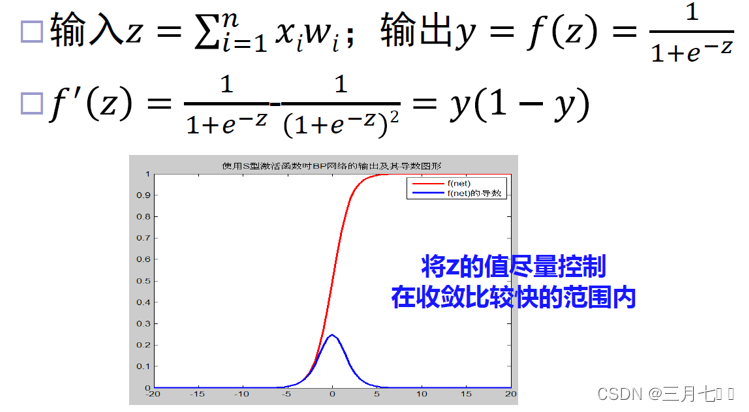
BP算法步骤:
①网络初始化:给各连接权值赋一个区间(-1,1)内的随机数,设定误差函数e,给定计算精确度
ε和最大学习次数M。
②随机选取第K个输入样本,及对应期望输出
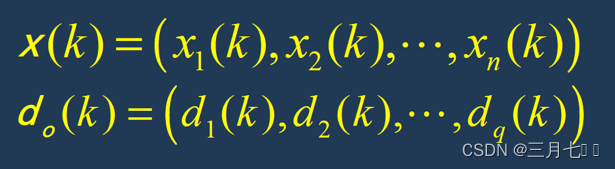
③计算各层各神经元的输入和输出

④计算误差函数对输出层权重的偏导数---链式微分法则
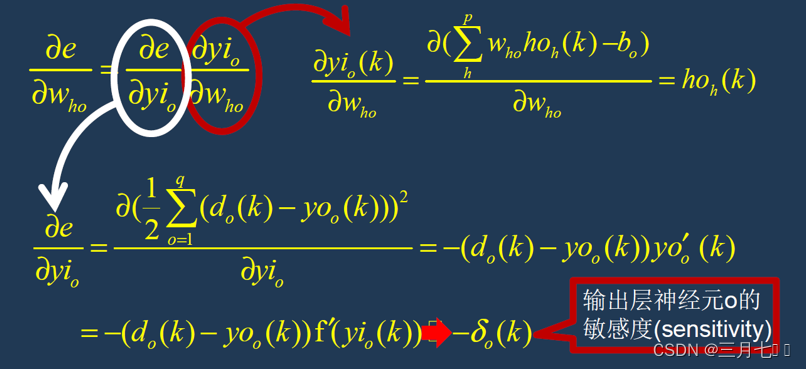

⑤计算误差函数对隐藏层权值的偏导数δ(k)
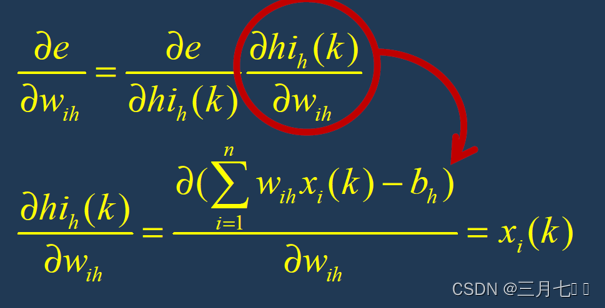

⑥修正隐藏层---输出层连接权值w(k)
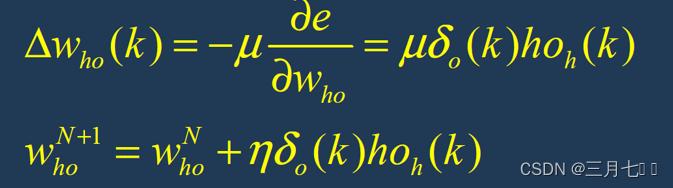
⑦修正输入层---隐藏层连接权值
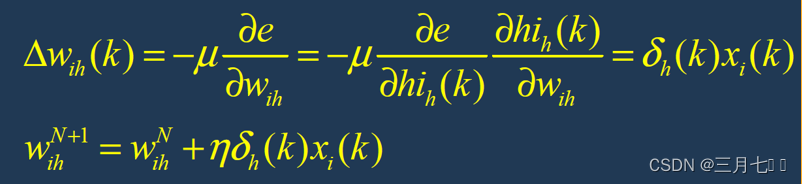
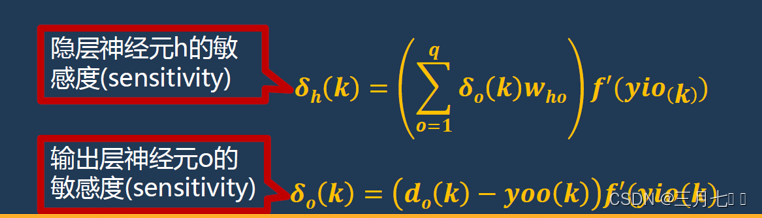
⑧计算全局误差
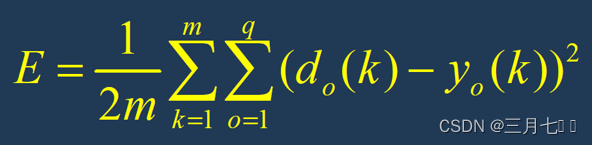
⑨判断网络误差是否满足要求
当误差达到预设精度或者学习次数大于设定的最大次数,则结束算法;
否则,选取下一个学习样本及对应的期望输出,返回到第三步,进入下一轮学习。
BP算法的直观解释:
①当误差对权值的偏导数大于0时,权值调整量为负,实际输出大于期望输出,权值向减少方向调
整,使得实际输出与期望输出的差减少。
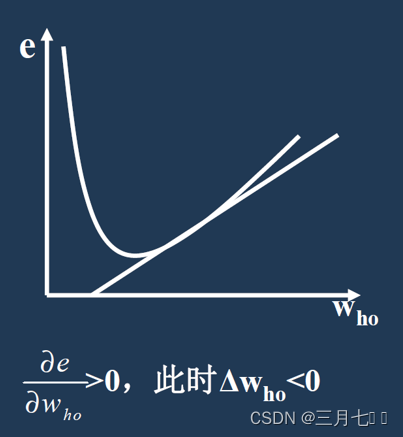
②当误差对权值的偏导数小于0时,权值调整量为正,实际输出小于期望输出,权值向增大方向调
整,使得实际输出与期望输出的差减少。

训练过程概述:
样本:(输入向量,理想输出向量)
①向前传播阶段
从样本集中取一个样本(Xp,Yp),将Xp输入到网络;
计算相应的实际输出Op:
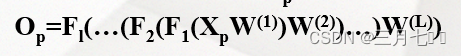
②向后传播阶段,误差传播阶段
计算实际输出Op与相应的理想输出Yp的差; 按极小化误差的方法调整权值矩阵。
网络中关于第p个样本的误差:
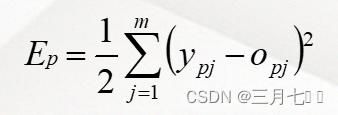
网络中关于整个样本集的误差:
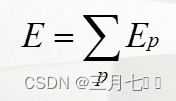
误差传播分析:
①输出层权的调整
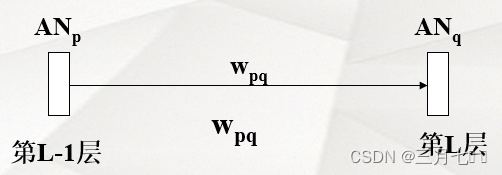

②隐藏层权的调整
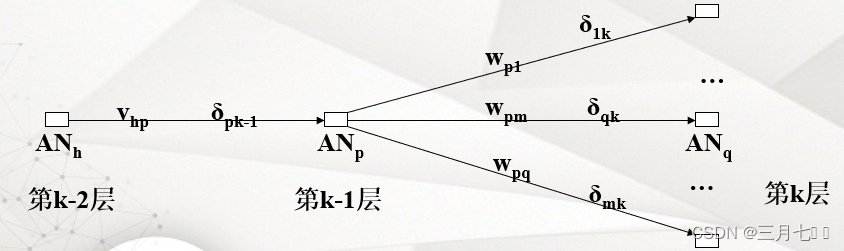
δpk-1的权值和δ1k、δ2k......δmk有关,不妨认为δpk-1通过权Wp1对δ1k做出贡献, 通过权Wp2对
δ2k做出贡献.......通过权Wpm对δmk做出贡献。
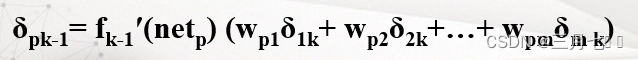
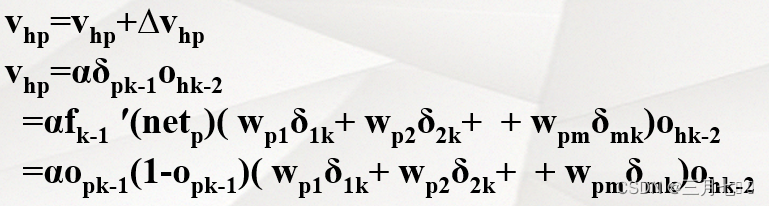
当ANj为输出层神经元时:

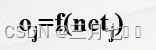
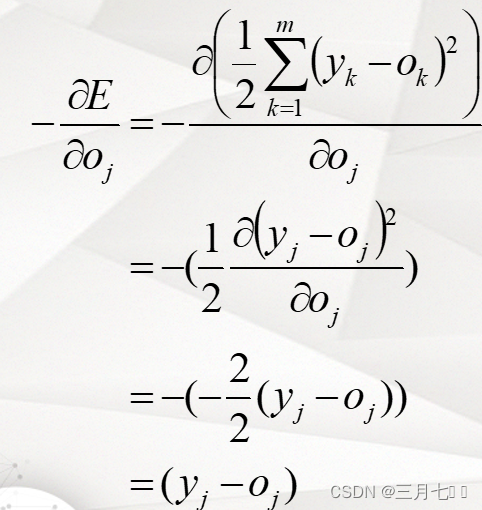
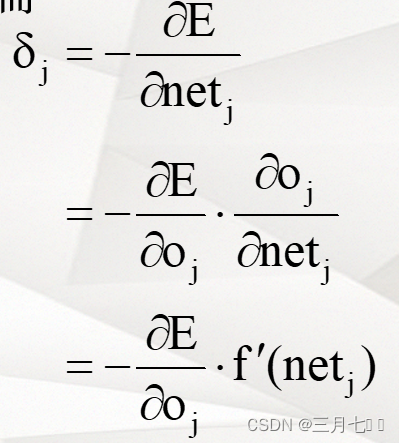
当ANj为隐藏层神经元时:


NETk是Oj下一级的神经元的网络输入。

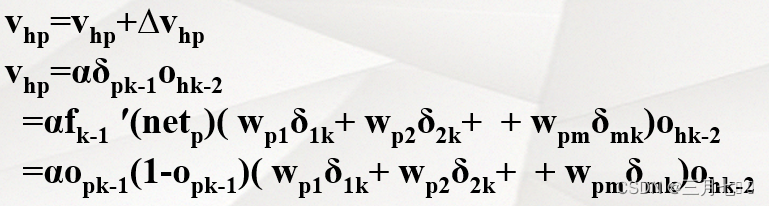
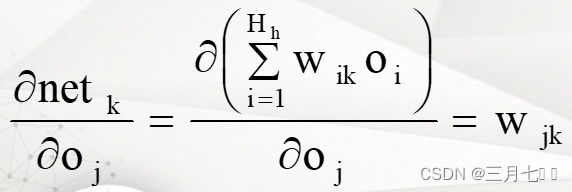
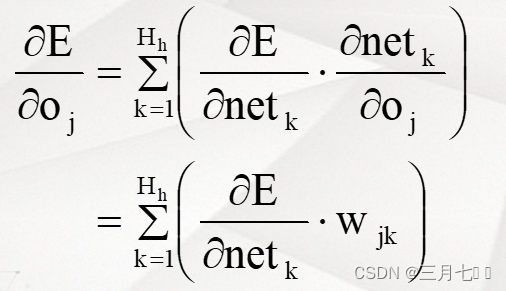
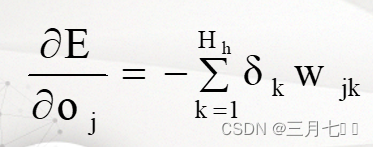
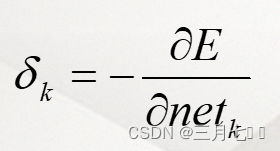
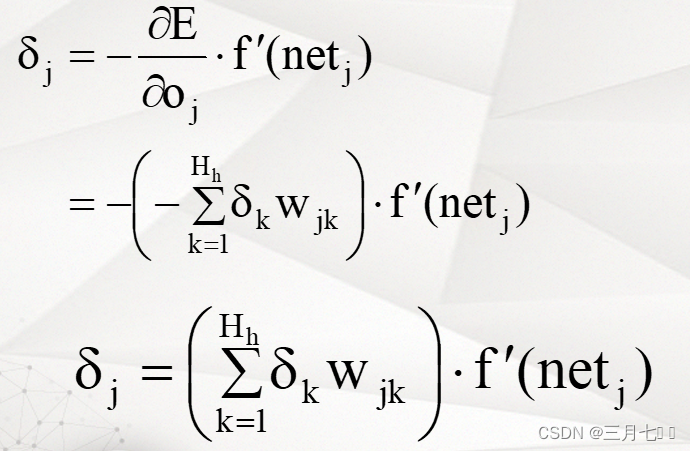
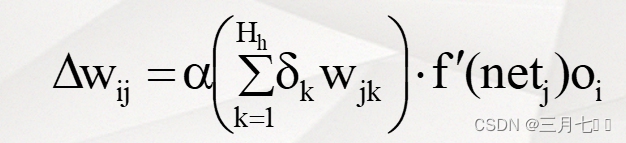
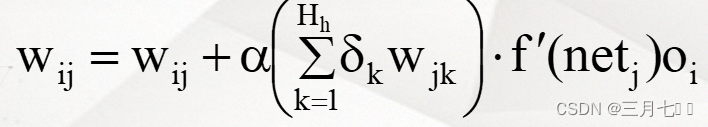
-
相关阅读:
第七章Redis_Jedis_测试
弱鸡记录一道模拟题
AWS SAA-C03 #152
虚拟机与主机(win10之间的通信)
热门Java开发工具IDEA入门指南——如何配置IDE
C++ 把类封装成静态链接库
IDEA中使用注解Test
cas:216300-12-8|1-丙基-3-甲基咪唑六氟磷酸盐[C3MIm]PF6离子液体分子量:125
驱动开发,udev机制创建设备节点的过程分析
十四.镜头知识之镜头色差
- 原文地址:https://blog.csdn.net/weixin_43961909/article/details/133386845