-
【C语言】快速排序

一、hoare版本
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
算法思想:
- 定义一个keyi存入随机一个数key的下标换到数组首元素,这里先直接默认key为数组首元素
- 定义一个left和一个right,分别存入数组首元素和尾元素的下标,用来移动交换
- 排升序我们让右边right先向左移动,找到比key的值小的元素则停下来换到left移动
- left向右移动,找到比key的值大的元素则停下
- 交换下标为left和right的元素
- 重复以上操作直到left与right相遇(相等)
- 交换key和下标为left的元素
- 此时key的左边都是比它小的数,右边都是比它大的数
- 再分别对左右序列进行以上的单趟排序,反复操作直到左右序列只有一个或者没有元素时停止操作,数列即可有序
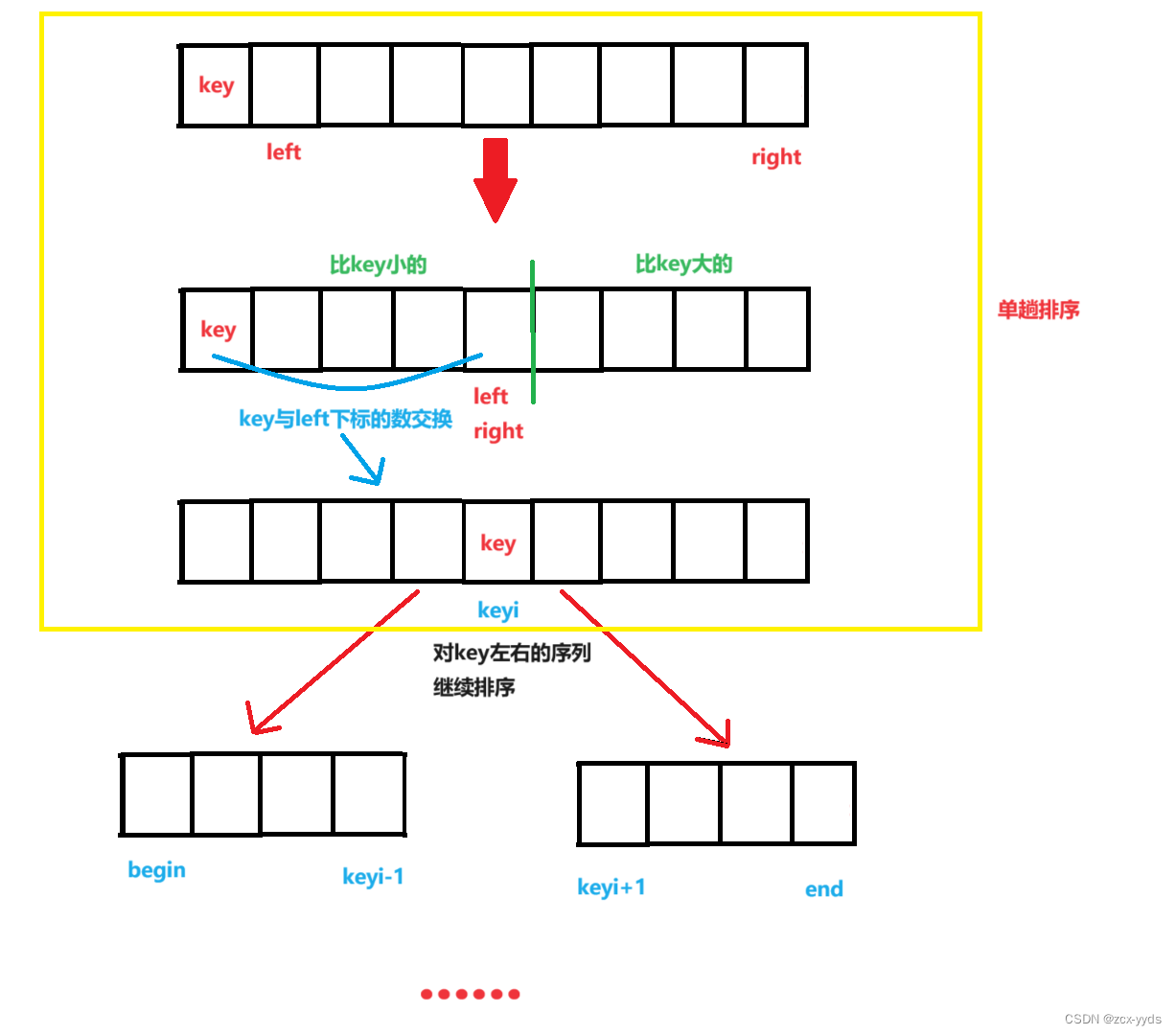
hoare版本单趟排序图示:

hoare版本代码:
//交换 void Swap(int* a, int* b) { int tmp = *a; *a = *b; *b = tmp; } //hoare版本 void QuickSort1(int* a, int begin, int end) { //递归结束条件 if (begin >= end) { return; } int keyi = begin; int left = begin; int right = end; //每趟排序直到左右相遇 while (left < right) { //右边先走,找到比key值小的 while (left < right && a[right] >= a[keyi]) { right--; } //right找到比key值小的之后换到left走,找到比key值大的 while (left < right && a[left] <= a[keyi]) { left++; } //交换 Swap(&a[left], &a[right]); } //将key值换到中间 Swap(&a[keyi], &a[left]); //更新key keyi = left; //对左右序列继续排序 QuickSort1(a, begin, keyi - 1); QuickSort1(a, keyi + 1, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
整体流程图:
二、挖坑法
挖坑法思想:
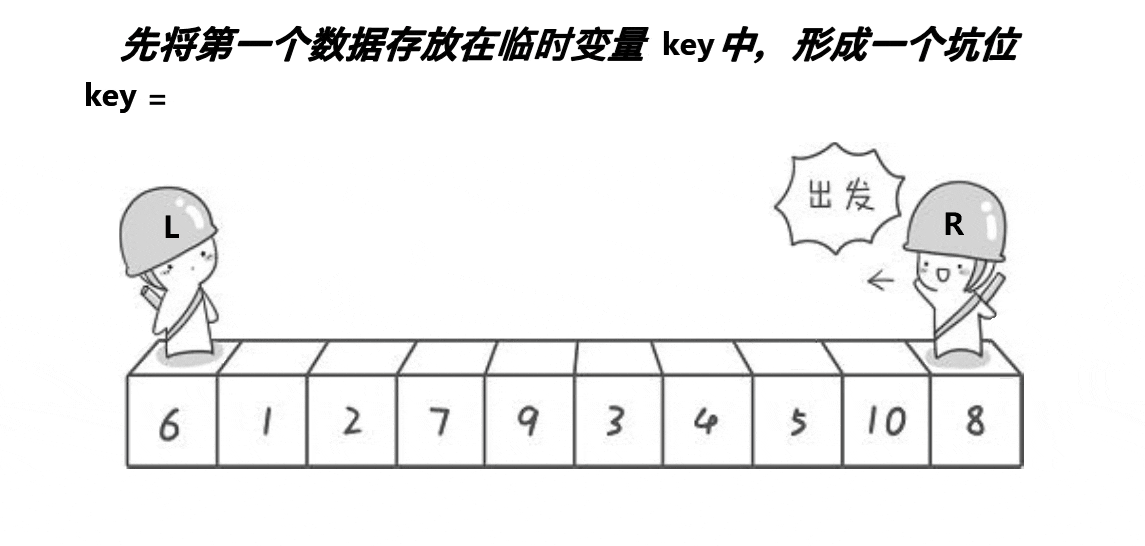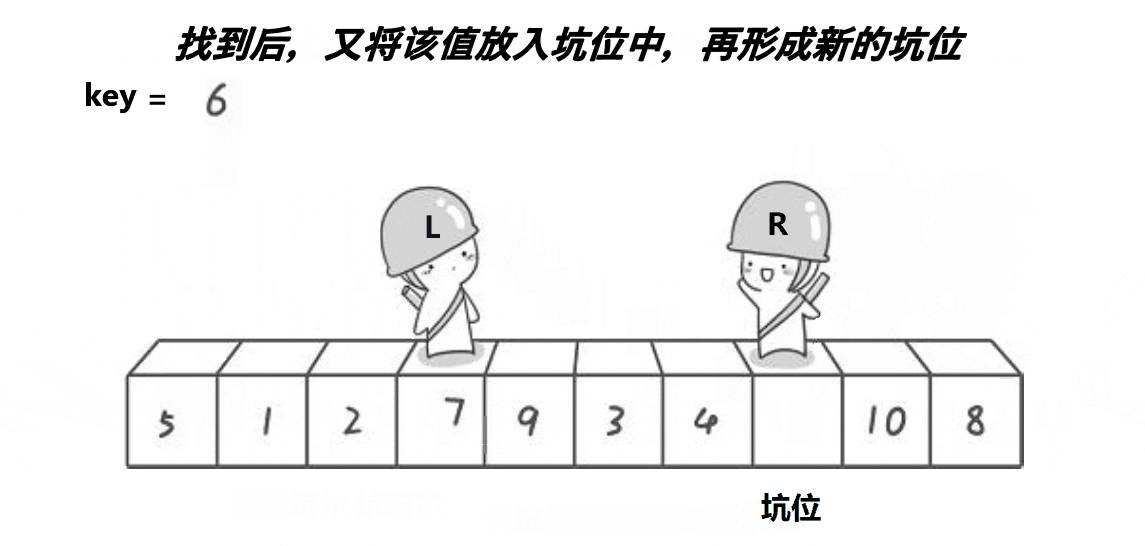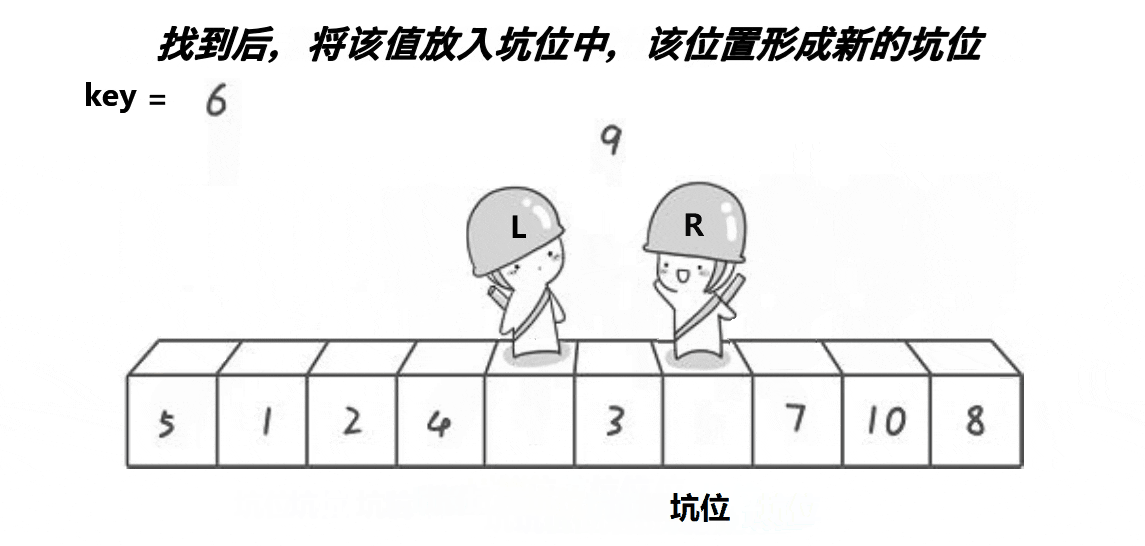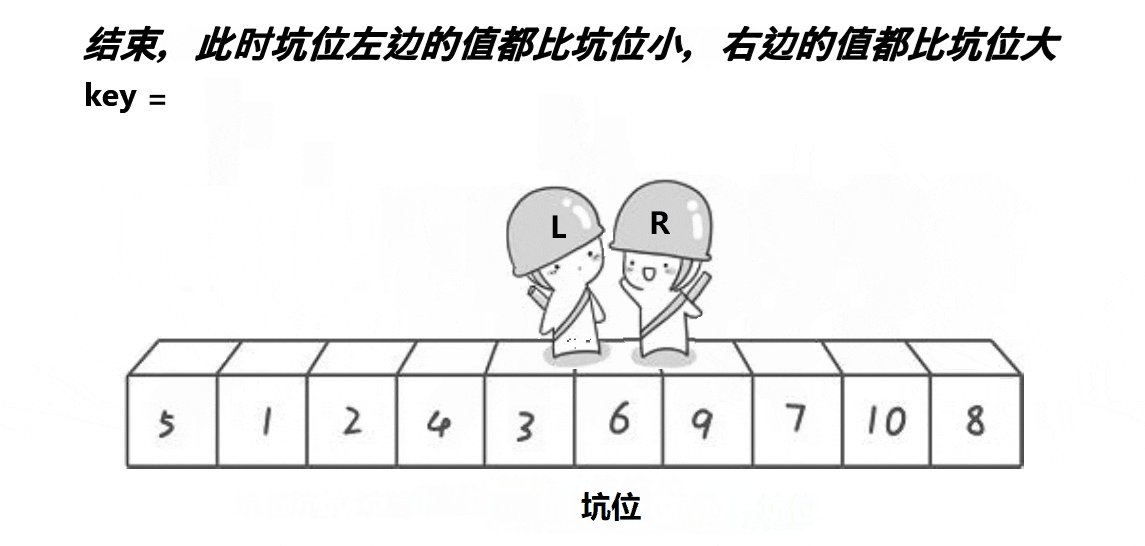
- 先将第一个数据存在变量key中,将此处作为最开始的坑位,用下标hole记录
- 然后right开始向前走,找到比key值小的元素后停下,将此元素放进坑里(下标为hole处),然后此处变为坑,hole变为此时的right
- 然后left开始向后移动,找到比key值大的元素后停下,将此元素放进坑里(下标为hole处),然后此处变为坑,hole变为此时的left
- 然后又换回right移动,如此反复直到left与right相遇(left与right相遇的地方一定是坑)
- 然后将key放入left与right相遇的位置,也就是坑的位置,此时hole左边都是小于等于它的,右边都是大于等于它的
- 如此单趟排序便结束,然后继续对hole左右序列继续反复执行以上操作,直到左右序列只有一个或者没有元素时停止操作,数列即可有序
挖坑法单趟排序图示:
挖坑法代码:
//挖坑法 void QuickSort2(int* a, int begin, int end) { //递归结束条件 if (begin >= end) { return; } int left = begin; int right = end; int key = a[left]; //坑最初与left一样在开始位置 int hole = left; //每趟排序直到左右相遇 while (left < right) { //右边先走,找到比key值小的 while (left < right && a[right] >= key) { right--; } //将right找到的比key小的元素放进坑中 a[hole] = a[right]; //更新坑的位置 hole = right; //然后左边走找到比key值大的元素停下来 while (left < right && a[left] <= key) { left++; } //将left找到的比key大的元素放进坑中 a[hole] = a[left]; //更新坑的位置 hole = left; } //将key放入坑中 a[hole] = key; //对左右序列继续排序 QuickSort2(a, begin, hole - 1); QuickSort2(a, hole+1, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
三、前后指针法
前后指针法思想:
- 定义一个keyi存入随机一个数key的下标换到数组首元素,这里先直接默认key为数组首元素
- 定义一个prev为开头元素的下标,定义一个cur为prev下一个元素的下标
- cur下标处的值与key比较,直到cur找到比key小的值则停下来
- prev下标后移一位然后与cur下标处的值交换,然后cur后移一位(prev相当于前面比key小的那些数的最后一个的下标,所以要先后移一位再交换)
- cur继续寻找比key小的值,反复执行直到cur的值大于n
- 将key与prev下标处的值交换,此时key左边都是小于等于它的,右边都是大于等于它的
- 如此单趟排序便结束,然后继续对key左右序列继续反复执行以上操作,直到左右序列只有一个或者没有元素时停止操作,数列即可有序
前后指针法单趟排序图示:

前后指针法代码:
//交换 void Swap(int* a, int* b) { int tmp = *a; *a = *b; *b = tmp; } //前后指针 void QuickSort3(int* a, int begin, int end) { //递归结束条件 if (begin >= end) { return; } int keyi = begin; int prev = begin; int cur = begin + 1; //每趟排序直到cur下标大于end while (cur <= end) { //cur找比key小的值 if (a[cur] < a[keyi] && ++prev != cur) { Swap(&a[cur], &a[prev]); } cur++; } //将key换到中间 Swap(&a[keyi], &a[prev]); //更新key的下标 keyi = prev; //对左右序列继续排序 QuickSort3(a, begin, keyi - 1); QuickSort3(a, keyi + 1, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
快速排序是一种不稳定的排序,它的时间复杂度为O(N*logN),但最坏可以达到O(N2) ,它的空间复杂度为O(logN)
四、非递归快排
以上三种方法都是采用了分治法递归实现的快排,其实快速排序也可以非递归实现,非递归实现快排需要利用栈来实现
思路:
将数组首尾下标存入栈中,在循环中依次取出作为left和right对数组进行排序,然后对得到的key的左右两边序列也进行相同的操作,其中左边为left到keyi-1,右边为keyi+1到right,这些下标的入栈顺序需要看取出的顺序,如下面代码中是先取出后面元素下标的,所以入栈时要先入后面的,因为栈的特点是先入后出。
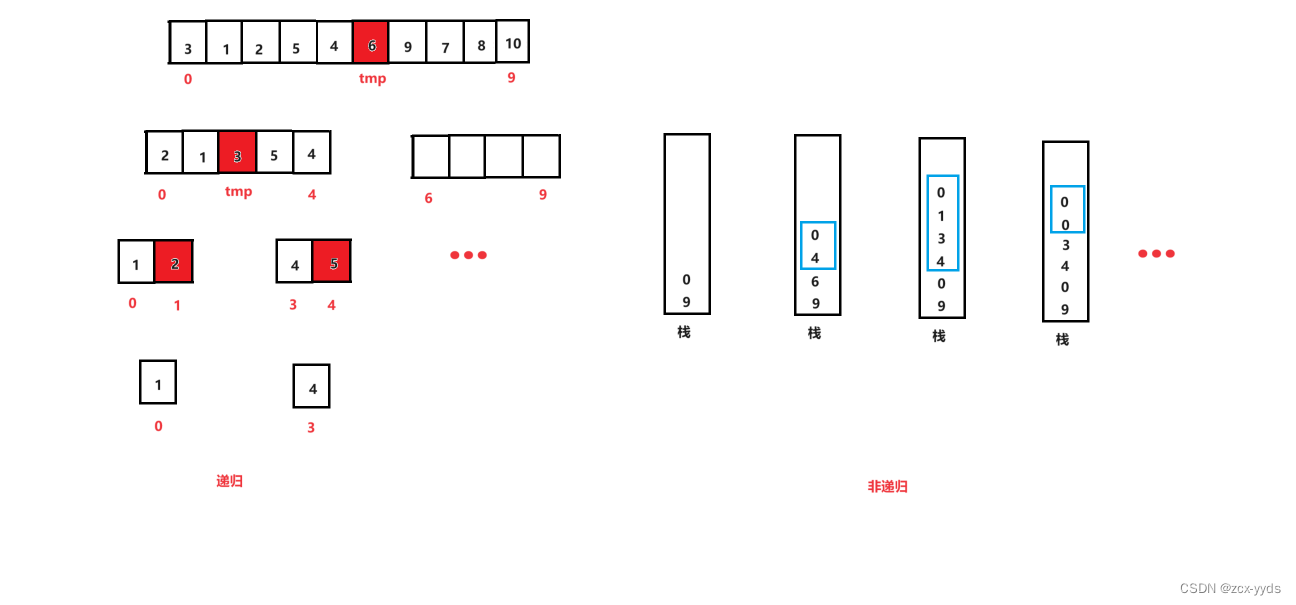
非递归快排代码:
(该代码中用到的栈需自己实现,C语言实现栈可参考:栈的实现)
//非递归快速排序 void QuickSortNonR(int* a, int begin, int end) { //创建一个栈 ST st; //初始化栈 STInit(&st); //插入尾元素下标 STPush(&st, end); //插入首元素下标 STPush(&st, begin); //栈为空停下 while (!STEmpty(&st)) { //取出栈顶元素作为left int left = STTop(&st); //取出后在栈中删除 STPop(&st); //取出栈顶元素作为right int right = STTop(&st); //取出后在栈中删除 STPop(&st); int keyi = begin; //每趟排序直到左右相遇 while (left < right) { //右边先走,找到比key值小的 while (left < right && a[right] >= a[keyi]) { right--; } //right找到比key值小的之后换到left走,找到比key值大的 while (left < right && a[left] <= a[keyi]) { left++; } //交换 Swap(&a[left], &a[right]); } //将key值换到中间 Swap(&a[keyi], &a[left]); //更新key的下标 keyi = left; // 当前数组下标样子 [left,keyi-1] keyi [keyi+1, right] //右边还有元素,按顺序插入right和keyi+1 if (keyi + 1 < right) { STPush(&st, right); STPush(&st, keyi + 1); } //左边还有元素,按顺序插入keyi-1和left if (left < keyi - 1) { STPush(&st, keyi - 1); STPush(&st, left); } } STDestroy(&st); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
五、快速排序优化
1、三数取中选key值
前面三种快速排序的方法起初都要随机选取一个值作为key,我们之前是直接默认为数组首元素的,这样不够随机,容易出现最坏的情况,使得它的时间复杂度接近O(N2),所以我们可以写一个函数来选取这个key,使得它比较随机,而不是直接为首元素。
三数取中:
在一个数组最前面、最后面,中间这三个位置的数中选出大小处于中间的数
// 三数取中 int GetMidi(int* a, int left, int right) { int mid = (left + right) / 2; if (a[left] > a[right]) { if (a[right] > a[mid]) { return right; } else if(a[mid]>a[right]&&a[mid]<a[left]) { return mid; } else { return left; } } else { if (a[left] > a[mid]) { return left; } else if (a[mid] > a[left] && a[mid] < a[right]) { return mid; } else { return right; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
在快排时用三数取中法选取key值再将它换到数组开头,可以有效避免出现最坏的情况,大大提升算法效率
2、小区间优化
当递归到数据较小时可以使用插入排序,使得小区间不再递归分割,降低递归次数
六、代码测试
//打印数组 void PrintArray(int* a, int n) { for (int i = 0; i < n; i++) { printf("%d ", a[i]); } printf("\n"); } void TestQuickSort1() { int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 }; QuickSort1(a, 0, sizeof(a) / sizeof(int) - 1); printf("hoare版本快速排序:\n"); PrintArray(a, sizeof(a) / sizeof(int)); } void TestQuickSort2() { int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 }; QuickSort2(a, 0, sizeof(a) / sizeof(int) - 1); printf("挖坑法快速排序:\n"); PrintArray(a, sizeof(a) / sizeof(int)); } void TestQuickSort3() { int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 }; QuickSort3(a, 0, sizeof(a) / sizeof(int) - 1); printf("前后指针法快速排序:\n"); PrintArray(a, sizeof(a) / sizeof(int)); } int main() { TestQuickSort1(); TestQuickSort2(); TestQuickSort3(); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38

-
相关阅读:
什么是特洛伊木马病毒?
应变计在工程中的角色:精准监测与安全保障的得力助手
Java泛型详解
《机器学习》- 第3章 线性模型
MES生产管理系统与供应链协同管理
Android---GC回收机制与分代回收策略
Redis缓存击穿、雪崩、穿透
PHPExcel 字母列不够用,针对 AA、AB、AC ... ZZ 这样的列
HTML期末大作业:基于HTML+CSS+JavaScript新能源汽车资讯门户网站
java运行linux命令时报错
- 原文地址:https://blog.csdn.net/zcxyywd/article/details/133270717
