【LeetCode算法系列题解】第71~75题

LeetCode 71. 简化路径（中等）

【题目描述】

给你一个字符串 path，表示指向某一文件或目录的 Unix 风格绝对路径（以 '/' 开头），请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点（..）表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，'//'）都被视为单个斜杠 '/'。 对于此问题，任何其他格式的点（例如，'...'）均被视为文件/目录名称。

请注意，返回的规范路径必须遵循下述格式：

• 始终以斜杠 '/' 开头。
• 两个目录名之间必须只有一个斜杠 '/'。
• 最后一个目录名（如果存在）不能以 '/' 结尾。
• 此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的规范路径。

【示例1】

输入：path = "/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。 
1
2
3

【示例2】

输入：path = "/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根目录是你可以到达的最高级。
1
2
3

【示例3】

输入：path = "/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。
1
2
3

【示例4】

输入：path = "/a/./b/../../c/"
输出："/c"
1
2

【提示】

$1\le path.length\le 3000$
path 由英文字母，数字，'.'，'/' 或 '_' 组成。
path 是一个有效的 Unix 风格绝对路径。

【分析】

---

文件结构是一个树结构，文件路径其实就是一个树上递归的过程，我们可以用栈的思想来模拟这个过程。若 path 的末尾不是 /，我们先添加一个 /，这样就能统一进行遍历处理，当遍历到 / 时对前面扫过的目录名 name 进行处理，一共会有以下几种情况：

• name == ".."：说明需要返回上级目录，则将结果目录结尾的 /xxx 删去；
• name == "." || name == ""：不需要进行任何操作；
• name == "xxx"：将 /xxx 添加至结果目录的末尾。

需要注意当最后的结果为空串时说明在根目录，需要返回 /。

---

【代码】

class Solution {
public:
    string simplifyPath(string path) {
        if (path.back() != '/') path += '/';
        string res, name;  //name为每两个'/'之间的字符串
        for (auto &c: path)
        {
            if (c != '/') { name += c; continue; }
            if (name == "..")
            {
                while (res.size() && res.back() != '/') res.pop_back();
                if (res.size()) res.pop_back();  // 删去'/'
            }
            else if (name != "." && name != "")  // 不为'.'和空串说明为文件名
                res += '/' + name;
            name.clear();
        }
        if (res.empty()) return "/";
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

LeetCode 72. 编辑距离（困难）

【题目描述】

给你两个单词 word1 和 word2，请返回将 word1 转换成 word2 所使用的最少操作次数。

你可以对一个单词进行如下三种操作：

• 插入一个字符；
• 删除一个字符；
• 替换一个字符。

【示例1】

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
1
2
3
4
5
6

【示例2】

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
1
2
3
4
5
6
7
8

【提示】

$0\le word1.length,word2.length\le 500$
word1 和 word2 由小写英文字母组成

【分析】

---

首先我们需要分析一下可能的操作，能够确定的是肯定不会有多余的操作，例如插入一个字符然后再将这个字符删去，或者改变一个字符后再将其变回去；且我们在考虑操作的时候可以不考虑顺序，例如先插入一个字符后再修改另一个字符与先修改再插入效果一样。

现在我们分析状态转移方程：

状态表示：

f[i][j] 表示将 word1[1, i] 变成 word2[1, j] 的所有按顺序操作（只考虑最后一个字符）的方案中操作次数的最小值。

状态计算：

• 删除 word1 的最后一个（第 $i$ 个）字符，使得 word1 == word2：说明在删除之前已经有 word1[1, i - 1] == word2[1, j]，即 f[i][j] = f[i - 1][j] + 1；
• 在 word1 的末尾添加一个字符，使得 word1 == word2：说明在添加之前已经有 word1[1, i] == word2[1, j - 1]，即 f[i][j] = f[i][j - 1] + 1；
• 将 word1[i] 变为 word2[j]，使得 word1 == word2：说明在修改之前已经有 word1[i, i - 1] == word2[1, j - 1]，即 f[i][j] = f[i - 1][j - 1] + 1/0，如果 word1[i] 已经等于 word2[j] 则不需要修改，因此可能是加0；
• 同以上三种情况，对 word2 进行操作也有三种情况分别为：f[i - 1][j] + 1、f[i][j - 1] + 1、f[i - 1][j - 1] + 1/0，可以发现与上面的情况重合了，因此最后只有三种转移方程。

注意，初始化的时候如果 word1 为空，word2 长度为 $j$，那么需要操作的最少次数为 $j$，同理反之也一样。

---

【代码】

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.size(), m = word2.size();
        word1 = ' ' + word1, word2 = ' ' + word2;
        vector<vector<int>> f(n + 1, vector<int>(m + 1));
        for (int i = 0; i <= n; i++) f[i][0] = i;
        for (int i = 0; i <= m; i++) f[0][i] = i;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
            {
                f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
                f[i][j] = min(f[i][j], f[i - 1][j - 1] + (word1[i] != word2[j]));  // 两个字符不相等时加1否则加0
            }
        return f[n][m];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

LeetCode 73. 矩阵置零（中等）

【题目描述】

给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。请使用原地算法。

【示例1】

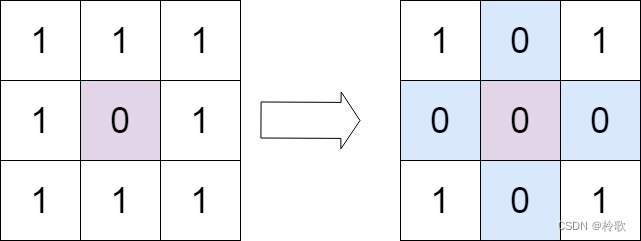
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
1
2

【示例2】

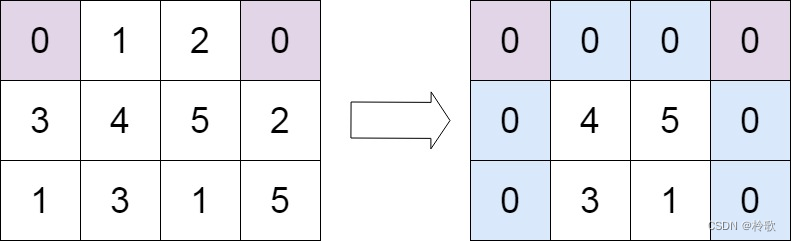
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
1
2

【提示】

$m==matrix.length$
$n==matrix[0].length$
$1\le m,n\le 200$
$-2^{31}\le matrix[i][j]\le 2^{31}-1$

【分析】

---

我们需要用原矩阵的第一行来记录每一列是否有0，用第一列来记录每一行是否有0。但是第一行与第一列是否有0的信息无法保存，因此还需要使用两个额外的变量来记录第一行与第一列是否有0。

---

【代码】

class Solution {
public:
    void setZeroes(vector<vector<int>>& g) {
        bool r0 = false, c0 = false;  // 第一行或者第一列是否有0
        for (int i = 0; i < g[0].size(); i++)  // 判断第一行是否有0
            if (!g[0][i]) { r0 = true; break; }
        for (int i = 0; i < g.size(); i++)  // 判断第一列是否有0
            if (!g[i][0]) { c0 = true; break; }
        for (int i = 1; i < g.size(); i++)  // 判断其余行是否有0
            for (int j = 1; j < g[0].size(); j++)
                if (!g[i][j]) { g[i][0] = 0; break; }
        for (int i = 1; i < g[0].size(); i++)  // 判断其余列是否有0
            for (int j = 1; j < g.size(); j++)
                if (!g[j][i]) { g[0][i] = 0; break; }
        for (int i = 1; i < g[0].size(); i++)  // 遍历第一行，将为0的元素所在的列置零
            if (!g[0][i])
                for (int j = 1; j < g.size(); j++)
                    g[j][i] = 0;
        for (int i = 1; i < g.size(); i++)  // 遍历第一列，将为0的元素所在的行置零
            if (!g[i][0])
                for (int j = 1; j < g[0].size(); j++)
                    g[i][j] = 0;
        if (r0) for (int i = 0; i < g[0].size(); i++) g[0][i] = 0;  // 第一行置零
        if (c0) for (int i = 0; i < g.size(); i++) g[i][0] = 0;  // 第一列置零
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

LeetCode 74. 搜索二维矩阵（中等）

【题目描述】

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非递减顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target，如果 target 在矩阵中，返回 true；否则，返回 false。

【示例1】

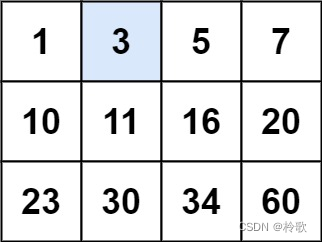
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true
1
2

【示例2】

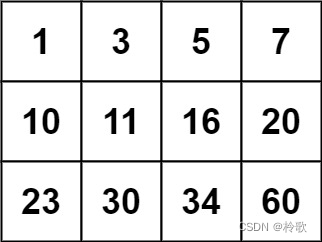
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false
1
2

【提示】

$1\le matrix.length,matrix[i].length\le 100$
$-10^4\le matrix[i][j],target\le 10^4$

【分析】

---

根据题意，该矩阵可以看成是一个一维的非递减数组，使用二分找出大于等于 target 的最小的数，然后判断是否等于 target 即可。

Tips：若原二维数组的行数与列数分别为 $n$ 和 $m$，则其一维数组形式下的下标 $idx$ 所对应的二维下标为 $[idx/m,idx\%m]$。

---

【代码】

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n = matrix.size(), m = matrix[0].size();
        int l = 0, r = n * m - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (matrix[mid / m][mid % m] >= target) r = mid;
            else l = mid + 1;
        }
        if (matrix[r / m][r % m] == target) return true;
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

LeetCode 75. 颜色分类（中等）

【题目描述】

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
我们使用整数 0、1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。

【示例1】

输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]
1
2

【示例2】

输入：nums = [2,0,1]
输出：[0,1,2]
1
2

【提示】

$1\le nums.length\le 300$
nums[i] 为 0、1 或 2

【分析】

---

本题的思路具有跳跃性，本质上是一个三指针算法，使用两个指针 $i,j(i>j)$ 从左往右扫描，还有一个指针 $k$ 从右往左扫描，然后我们要使得 nums[0, j - 1] 都为0，nums[j, i - 1] 都为1，nums[k + 1, n - 1] 都为2。

我们使用指针 $i$ 进行遍历，nums[i] 有以下三种情况：

• nums[i] == 0：由于 nums[j] == 1，因此我们交换 nums[i] 和 nums[j]，然后分别将指针 $i$ 和 $j$ 向后移动一位；
• nums[i] == 1：直接将指针 $i$ 向后移动一位即可；
• nums[i] == 2：交换 nums[i] 和 nums[k]，但是此时从 $k$ 交换过来的数不一定是1，因此指针 $i$ 无需移动，将 $k$ 向前移动一位即可。

---

【代码】

class Solution {
public:
    void sortColors(vector<int>& nums) {
        for (int i = 0, j = 0, k = nums.size() - 1; i <= k;)
        {
            if (nums[i] == 0) swap(nums[i++], nums[j++]);
            else if (nums[i] == 1) i++;
            else swap(nums[i], nums[k--]);
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11