重要采样的原理与实现

重要采样的原理与实现

1. 引言

在雷达系统性能仿真时，由于雷达系统对虚警概率的要求，实现一定精度的仿真，所需要的Monte-Carlo实验次数将非常地高。重要采样可以在保障精度的前提下，大大降低Monte-Carlo实验次数。

网上有很多关于重要采样的原理介绍，但总体感觉过于抽象，很不好理解。有幸检索到钱键民在1984年写的一篇文章，以雷达从业者的角度介绍了重要采样。他的介绍非常的直观，下面就将该论文的内容做一简单的介绍，希望能够帮助到需要有朋友。

2. 雷达虚警概率模拟及模拟精度

雷达的虚警概率是指雷达只接收噪声时却报告存在目标的概率，即目标是虚假的概率。假设目标不存在时的雷达视频信号的概率密度函数为，检测门限为，则虚警概率为

$p_{fa}=\int_T p(y)dy$

也就是说，虚警概率是噪声高于检测门限的概率。

模拟雷达系统的虚警概率时，通常是根据概率密度函数产生一个随机数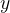，将其与检测门限进行比较，得到一个新的随机变量

$Z_T(y)=\left\{\begin{array}{ll} 1 & y\geqslant T\\ 0 & y <T \end{array}\right.$

所以，的数学期望为

$E[Z_T(y)]=p_{fa}$

又因为

$E[Z_T^2(y)]=p_{fa}$

所以，的方差为

$D[Z_T(y)]=p_{fa}-p_{fa}^2\approx p_{fa}$

数学期望的无偏估计为

$\hat{p}_{fa}=\frac{1}{N}\sum_{n=1}^NZ_T(y_n)$

因此，可以获得估计 $\hat{p}_{fa}$ 的均值与方差分别为

$E[\hat{p}_{fa}]=p_{fa}\\ D[\hat{p}_{fa}]=\frac{1}{N}D[Z_T(y)]=\frac{1}{N}p_{fa}$

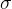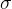反映一个估计量优劣的标准有两个：一个是准确度，或称可信度，由估计量的数学期望与真值之间的差值来反映；另一个是精确度，也叫可靠度，由估计量的标准差 $\sigma$ 来反映， $\sigma$ 描述了估计量在其均值附近的散布程度。

对于虚警概率估计 $\hat{p}_{fa}$ ，其是 $p_{fa}$ 的无偏估计，因此从准确度的角度，该估计量是最佳的。从精确度的角度，通常要求估计量的标准差比被估计量的标准差小一个数量级，即

$\frac{\sqrt{D[\hat{p}_{fa}]}}{\sqrt{D[Z_T(y)]}}=10^{-1}$

将上式整理可得
相关阅读:
Open3D 泊松盘网格采样
 C++版本的OpenCV 5.x编译生成opencv-python==5.x(GPU版本)接口并进行调用
 关于Ubuntu18.04安装后没有gcc、make、网卡驱动的问题总结以及解决办法
 构建 App 的方法
 【神印王座】两位新老婆登场！龙皓晨神勇救美，采儿却大发醋意！
一文搞懂 MySQL 日志
 （仿牛客社区项目）Java开发笔记7.8：将文件上传至服务器
 MFC绘制二维图形【1】—— 使用映射模式函数自定义坐标系
 unity3d-Animation&&Animator接口（基本使用）
ip伪装..
原文地址：https://blog.csdn.net/weixin_42428226/article/details/133173639

1. 引言

2. 雷达虚警概率模拟及模拟精度