数值微分比较

对于序列 { x n } = x 1 , x 2 , ⋯   , x n \{x_n\}= x_1, x_2, \cdots, x_n {xn​}=x1​,x2​,⋯,xn​，求其导数 { x n ′ } \{x'_n\} {xn′​}。

一、精度 $O(h)$

$$x_k^{\prime }=\{\begin{array}{l}\frac{x_2-x_1}{h},k=1\\ \frac{x_k-x_{k-1}}{h},k=2,3,\cdots ,n\end{array}$$

其中，对$k=1$时进行处理，保证导数序列长度也为 $n$。

二、精度 $O(h^2)$

也即中心微分算法

$$x_k^{\prime }=\{\begin{array}{l}\frac{x_2-x_1}{h},k=1\\ \frac{x_{k+1}-x_{k-1}}{2h},k=2,3,\cdots ,n-1\\ \frac{x_n-x_n-1}{h},k=n\end{array}$$

三、精度 $O(h^4)$

$$x_k^{\prime }=\{\begin{array}{l}\frac{x_2-x_1}{h},k=1\\ \frac{x_3-x_1}{2h},k=2\\ \frac{-x_{k+2}+8x_{k+1}-8x_{k-1}+x_{k-2}}{12h},k=3,\cdots ,n-2\\ \frac{x_n-x_{n-2}}{2h},k=n-1\\ \frac{x_n-x_n-1}{h},k=n\end{array}$$

四、比较

设 $x=\sin (t)$，真实导数为 $\cos (t)$，离散采样作比较。当 $T_s=0.1$ 时如下，可见直接微分精度较低。

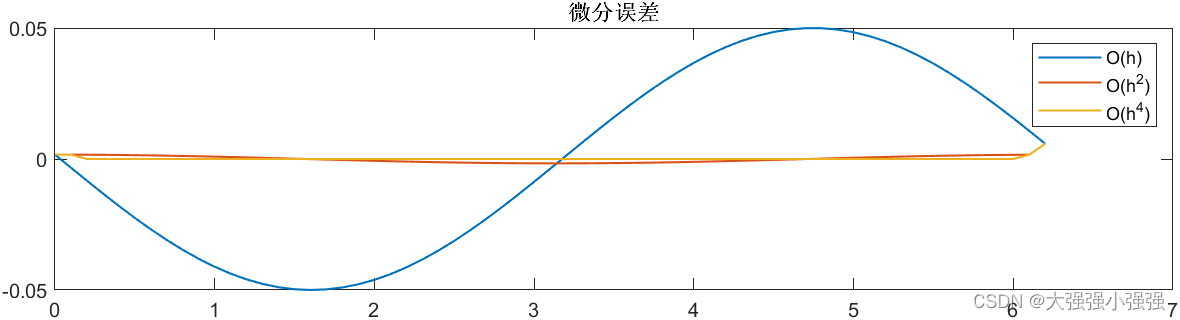
采样时间为 $T_s=1$ 时如下

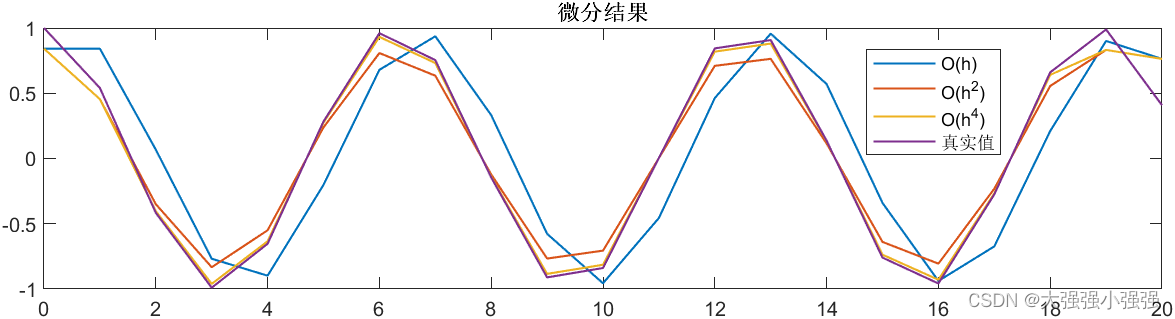
结论：很多时候中心微分就够了

代码如下

Ts = 1;
t = 0:Ts:20;
N = length(t);
t = reshape(t, [N,1]);

x = sin(t);
dx = cos(t);

dx1 = diff_1st(x, Ts);
dx2 = diff_2nd(x, Ts);
dx3 = diff_4th(x, Ts);


subplot(211);plot(t, dx1, t, dx2, t, dx3, t, dx, 'linewidth',1)
legend('O(h)', 'O(h^2)', 'O(h^4)', '真实值')
title('微分结果')

subplot(212);plot(t, dx-dx1, t, dx-dx2, t, dx-dx3, 'linewidth',1)
legend('O(h)', 'O(h^2)', 'O(h^4)')
title('微分误差')

function dx = diff_1st(x, dt)
    dx = (x(2:end) - x(1:end-1)) / dt;
    dx = [dx(1); dx];
end

function dx = diff_2nd(x, dt)   
    dx = (x(3:end) - x(1:end-2)) / (2*dt);
    dx1 = (x(2)-x(1)) / dt;
    dxend = (x(end)-x(end-1)) / dt;
    dx = [dx1; dx; dxend];
end

function dx = diff_4th(x, dt)
    dx = (-x(5:end) + 8 * x(4:end-1) - 8 * x(2:end-3) + x(1:end-4)) / (12 * dt);
    dx2 = (x(3) - x(1)) / (2*dt);
    dx1 = (x(2) - x(1)) / dt;
    dx_end2 = (x(end) - x(end-2)) / (2*dt);
    dx_end1 = (x(end) - x(end-1)) / dt;

    dx = [dx1; dx2; dx; dx_end2;dx_end1];
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42