回归预测 | MATLAB实现RUN-XGBoost龙格库塔优化极限梯度提升树多输入回归预测

回归预测 | MATLAB实现RUN-XGBoost多输入回归预测

预测效果

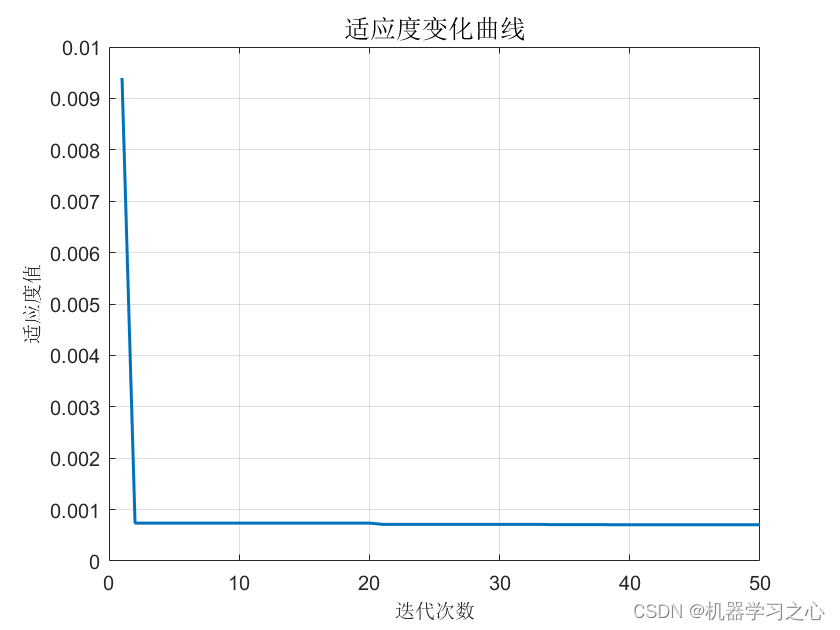
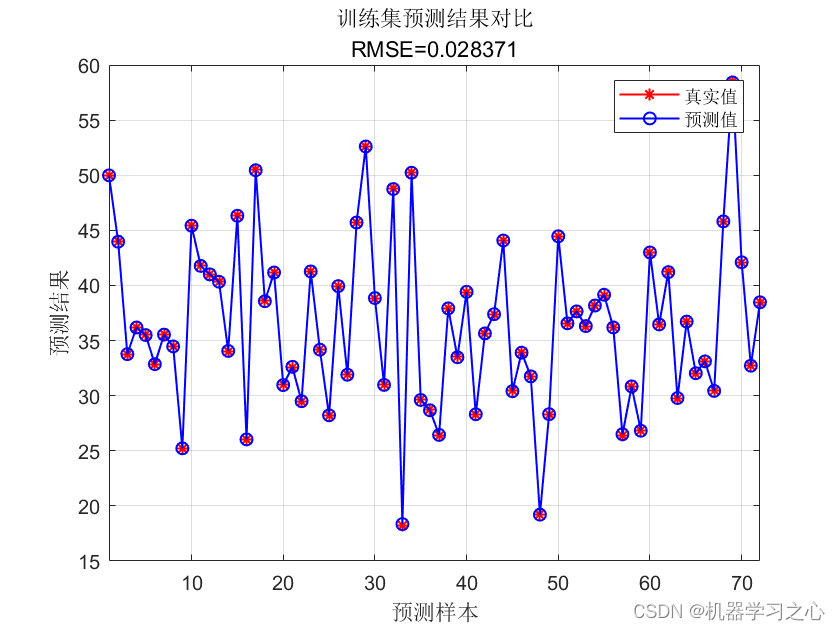
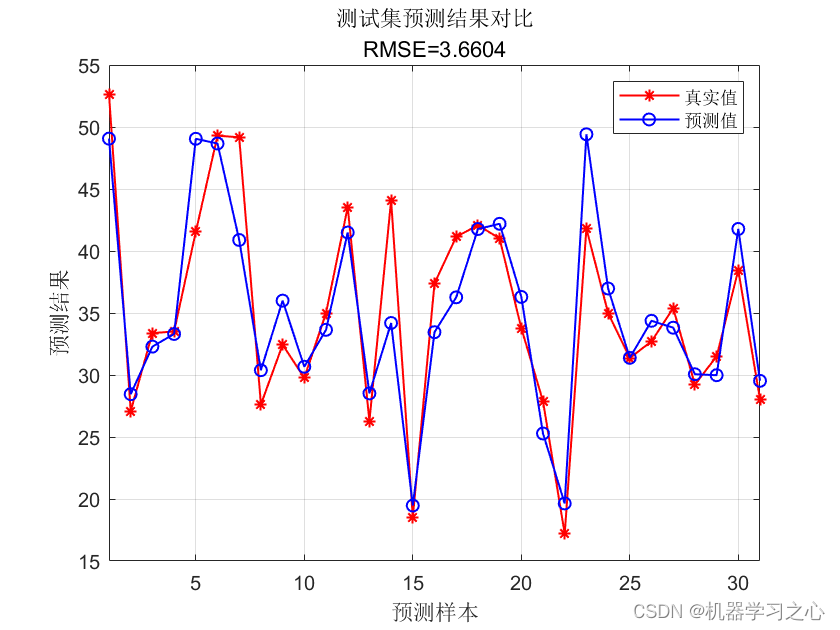
基本介绍

MATLAB实现RUN-XGBoost多输入回归预测（完整源码和数据）
1.龙格库塔优化XGBoost，数据为多输入回归数据，输入7个特征，输出1个变量,程序乱码是由于版本不一致导致，可以用记事本打开复制到你的文件。
2.运行环境MATLAB2018b及以上。
3.附赠案例数据可直接运行main一键出图～
4.注意程序和数据放在一个文件夹。
5.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。

程序设计

• 完整源码和数据获取方式（资源出下载）：MATLAB实现RUN-XGBoost多输入回归预测。

%% Main Loop of RUN 
it=1;%Number of iterations
while it<Max_iteration
    it=it+1;
    f=20.*exp(-(12.*(it/Max_iteration))); % (Eq.17.6) 
    Xavg = mean(X);               % Determine the Average of Solutions
    SF=2.*(0.5-rand(1,pop)).*f;    % Determine the Adaptive Factor (Eq.17.5)
    
    for i=1:pop
            [~,ind_l] = min(Cost);
            lBest = X(ind_l,:);   
            
            [A,B,C]=RndX(pop,i);   % Determine Three Random Indices of Solutions
            [~,ind1] = min(Cost([A B C]));
            
            % Determine Delta X (Eqs. 11.1 to 11.3)
            gama = rand.*(X(i,:)-rand(1,dim).*(ub-lb)).*exp(-4*it/Max_iteration);  
            Stp=rand(1,dim).*((Best_pos-rand.*Xavg)+gama);
            DelX = 2*rand(1,dim).*(abs(Stp));
            
            % Determine Xb and Xw for using in Runge Kutta method
            if Cost(i)<Cost(ind1)                
                Xb = X(i,:);
                Xw = X(ind1,:);
            else
                Xb = X(ind1,:);
                Xw = X(i,:);
            end

            SM = RungeKutta(Xb,Xw,DelX);   % Search Mechanism (SM) of RUN based on Runge Kutta Method
                        
            L=rand(1,dim)<0.5;
            Xc = L.*X(i,:)+(1-L).*X(A,:);  % (Eq. 17.3)
            Xm = L.*Best_pos+(1-L).*lBest;   % (Eq. 17.4)
              
            vec=[1,-1];
            flag = floor(2*rand(1,dim)+1);
            r=vec(flag);                   % An Interger number 
            
            g = 2*rand;
            mu = 0.5+.1*randn(1,dim);
            
            % Determine New Solution Based on Runge Kutta Method (Eq.18) 
            if rand<0.5
                Xnew = (Xc+r.*SF(i).*g.*Xc) + SF(i).*(SM) + mu.*(Xm-Xc);
            else
                Xnew = (Xm+r.*SF(i).*g.*Xm) + SF(i).*(SM)+ mu.*(X(A,:)-X(B,:));
            end  
            
        % Check if solutions go outside the search space and bring them back
        FU=Xnew>ub;FL=Xnew<lb;Xnew=(Xnew.*(~(FU+FL)))+ub.*FU+lb.*FL; 
        CostNew=fobj(Xnew);
        
        if CostNew<Cost(i)
            X(i,:)=Xnew;
            Cost(i)=CostNew;
        end
%% Enhanced solution quality (ESQ)  (Eq. 19)      
        if rand<0.5
            EXP=exp(-5*rand*it/Max_iteration);
            r = floor(Unifrnd(-1,2,1,1));

            u=2*rand(1,dim); 
            w=Unifrnd(0,2,1,dim).*EXP;               %(Eq.19-1)
            
            [A,B,C]=RndX(pop,i);
            Xavg=(X(A,:)+X(B,:)+X(C,:))/3;           %(Eq.19-2)         
            
            beta=rand(1,dim);
            Xnew1 = beta.*(Best_pos)+(1-beta).*(Xavg); %(Eq.19-3)
            
            for j=1:dim
                if w(j)<1 
                    Xnew2(j) = Xnew1(j)+r*w(j)*abs((Xnew1(j)-Xavg(j))+randn);
                else
                    Xnew2(j) = (Xnew1(j)-Xavg(j))+r*w(j)*abs((u(j).*Xnew1(j)-Xavg(j))+randn);
                end
            end
            
            FU=Xnew2>ub;FL=Xnew2<lb;Xnew2=(Xnew2.*(~
                if rand<w(randi(dim)) 
                    SM = RungeKutta(X(i,:),Xnew2,DelX);
                    Xnew = (Xnew2-rand.*Xnew2)+ SF(i)*(SM+(2*rand(1,dim).*Best_pos-Xnew2));  % (Eq. 20)
                    
                    FU=Xnew>ub;FL=Xnew<lb;Xnew=(Xnew.*(~(FU+FL)))+ub.*FU+lb.*FL;
                    CostNew=fobj(Xnew);
                    
                    if CostNew<Cost(i)
                        X(i,:)=Xnew;
                        Cost(i)=CostNew;
                    end
                end
            end
        end
% End of ESQ         
%% Determine the Best Solution
        if Cost(i)<Best_score
            Best_pos=X(i,:);
            Best_score=Cost(i);
        end

    end
% Save Best Solution at each iteration    
curve(it) = Best_score;
disp(['it : ' num2str(it) ', Best Cost = ' num2str(curve(it) )]);

end

end


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501