-
机器学习西瓜书+南瓜书吃瓜教程学习笔记第四章决策树
1、算法原理
从逻辑角度,一堆if else语句的组合
从集合角度,根据某种准则划分特征空间
最终目的:将样本越分越“纯”
决策树是基于树结构来进行决策的
例如,我们对“这是好瓜吗?”这样的问题进行决策时,通常会进行一系列的判断或“子决策”:我们先看“它是什么颜色?”,如果是“青绿色”,则我们再看“它的根蒂是什么形态?”,如果是“蜷缩”,我们再判断“它敲起来是什么声音?”,最后,我们得出最终决策:这是个好瓜,这个决策过程如图:
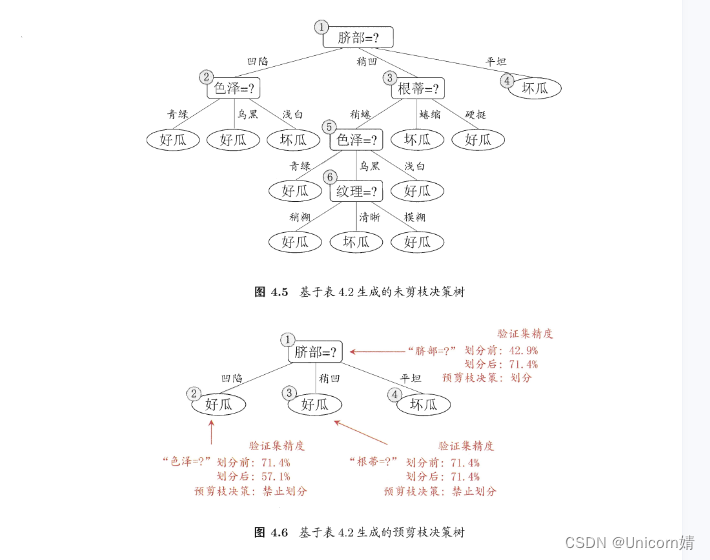
显然,决策过程是一个递归的过程其最终结论对应了我们所希望的判定结果,例如“是”或“不是”好瓜。
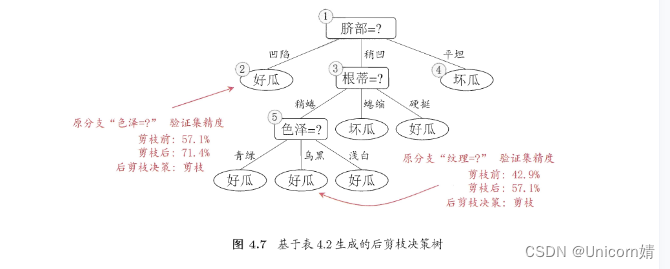
决策树学习的母的是为了产生一颗泛化能力强,即处理未见示例能力强,即处理未见示例能力强的决策树,其基本流程遵循简单且直观的“分而治之”策略。

信息熵(自信息的期望):度量随机变量X的不确定性,信息熵越大越不确定
H ( x ) = E [ I ( x ) ] = − ∑ x p ( x ) log b p ( x ) H\left( x\right) =E\left[ I\left( x\right) \right] =-\sum _{x}p\left( x\right) \log _{b}p\left( x\right) H(x)=E[I(x)]=−∑xp(x)logbp(x)

条件熵(Y的信息熵关于概率分布X的期望):在一直X后Y的不确定性
H ( Y ∣ X ) = ∑ x p ( x ) H ( Y ∣ X = x ) H\left( Y| X\right) =\sum _{x}p\left( x\right) H( Y| X= x) H(Y∣X)=∑xp(x)H(Y∣X=x)
在已知属性a的取值后,样本集合D的条件熵为:
∑ v = 1 ν ∣ D v ∣ ∣ D ∣ E n t ( D v ) \sum ^{\nu }_{v=1}\dfrac{\left| D^{v}\right| }{\left| D\right| }Ent\left( D^{v}\right) ∑v=1ν∣D∣∣Dv∣Ent(Dv)
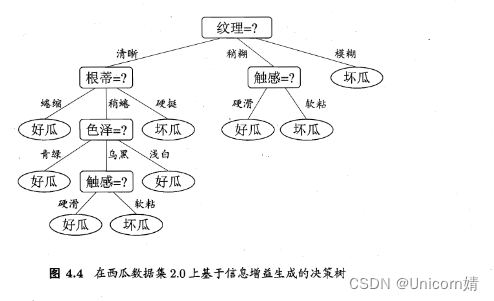
信息增益:在已知属性(特征)a的取值后y的不确定性减少的量,也即纯度的提升
G a i n ( D , a ) = E n t M − ∑ v = 1 v ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain\left( D,a\right) =EntM-\sum ^{v}_{v=1}\dfrac{\left| D^{v}\right| }{\left| D\right| }Ent\left( D^{v}\right) Gain(D,a)=EntM−∑v=1v∣D∣∣Dv∣Ent(Dv)
也就是信息熵(大)- 条件熵=信息增益

信息增益准则对可能取值数目较多的属性有所偏好(例如“编号”这个较为极端的例子,不过其本质原因不是取值数目过多,而是每个取值里面所包含的样本量太少),为减少这种偏好可能带来的不利影响,C4.5决策树选择使用“增益率”代替“信息增益”,增益率定义为
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain\_ ratio\left( D,a\right) =\dfrac{Gain\left( D,a\right) }{IV\left( a\right) } Gain_ratio(D,a)=IV(a)Gain(D,a)
其中

C4.5决策树并未完全使用“增益率”代替“信息增益”,而是采用一种启发式的方法:先选出信息增益高于平均水平的属性,然后再从中选择增益率最高的。



三种算法的比较
ID3:倾向于选择水平数量较多的变量(偏向数值比较多的特征),可能导致训练得到一个庞大且
深度浅的树;另外输入变量必须是分类变量(连续变量必须离散化)。
C4.5在ID3的基础上选择了信息增益率替代信息增益,它更偏心于数量较少的变量(属性)。同
时,采用二分法来处理连续值的特征,但是生成树浅的问题还是存在,且只能处理分类问题。
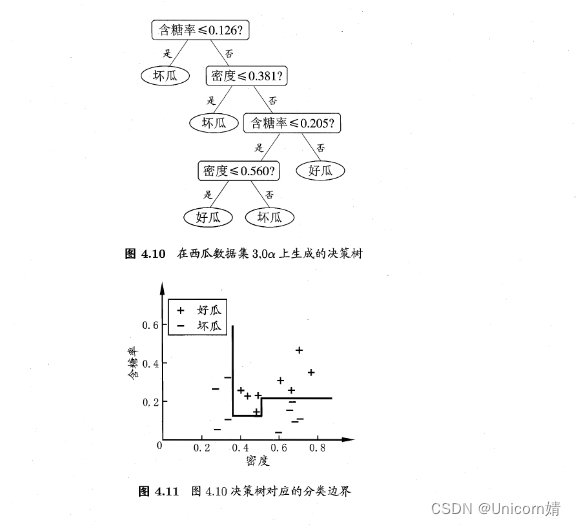
CART以基尼系数替代熵,划分规则是最小化不纯度而不是最大化信息增益(率)。同时只允许生
成二叉树,增加树的深度,而且可以处理连续特征和回归问题。
scikit-learn实现的决策树更默认是CRAT决策树,即判断标准默认为基尼系数。也可以手动修改,
比如节点的划分标准也可以选择采用熵来划分。 -
相关阅读:
亚信安慧AntDB数据并行加载工具的实现(二)
如何绘制思维导图
FW:HP笔记本type-c接口失效
数学分析:傅里叶三角级数
【LeetCode热题100】--74.搜索二维矩阵
【Proteus仿真】【STM32单片机】出租车计价器
Oracle技术分享 创建外键报错ORA-00906
贪心——区间问题
【数组】非递增的最小子序列 计数排序
231.2的幂
- 原文地址:https://blog.csdn.net/m0_68165821/article/details/133144793