Python深度学习入门 - - Transformers网络学习笔记

前言

---

一、Transformers架构原理

Transformer 架构与传统循环神经网络RNN、LSTM相比具有并行计算、自注意力机制、位置编码和多头注意力等方面的差异。这些差异使得 Transformer 在处理长序列、建模上下文关系和并行计算方面表现出更强的能力，成为自然语言处理和其他序列任务中的重要架构。

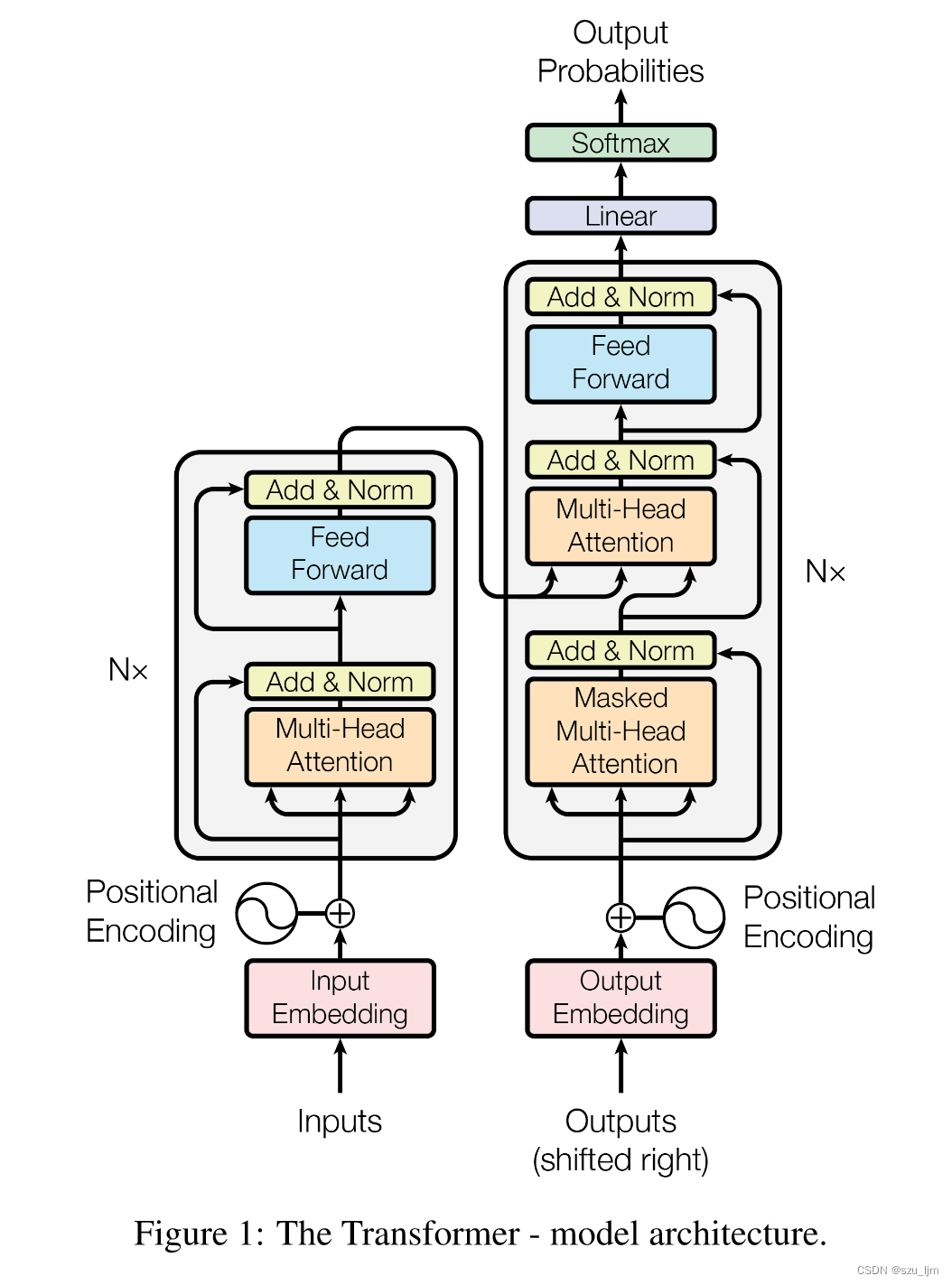
编码器由 6 个相同的层堆叠组成。每一层都有两个子层。第一个是多头自注意机制，第二个是简单的位置全连接前馈网络。我们在两个子层的每个周围都采用了残差连接，然后进行层归一化。

解码器也由6 个相同的层堆叠组成。除了每个编码器层中的两个子层外，解码器还插入了第三个子层，对编码器堆栈的输出执行多头关注。与编码器类似，我们在每个子层周围采用残差连接，然后进行层归一化。

1、自注意力层（Self-Attention）

Transformers架构中加入了自注意力层，自注意力层相比之前GRU（门控循环单元），能并行地关注更多序列信息，这使得Transformers网络不再简单地依据前后依赖关系来建模序列信息的相关性，Transformers网络能关注更远的序列信息，从而捕获建模更长的时序关系。

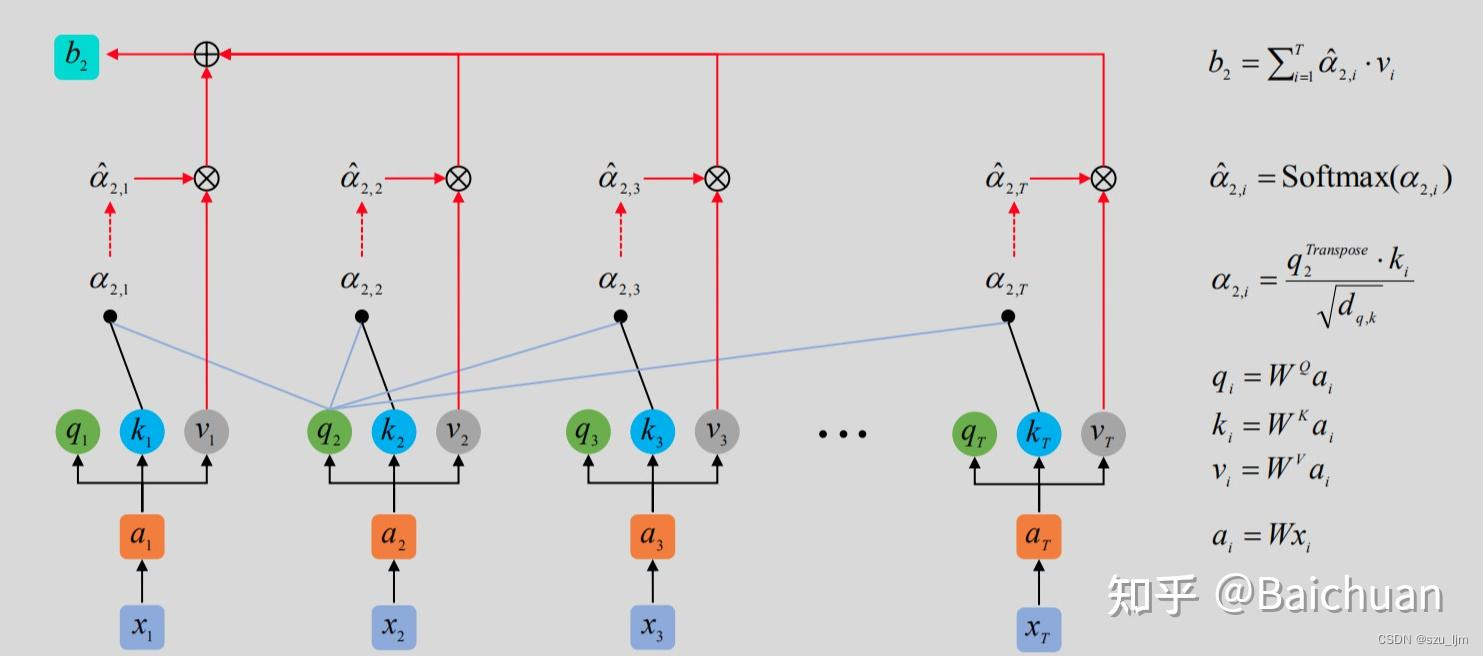
假设输入序列为 $X\in {\mathbb{R}}^{L\times d_{\text{model}}}$，其中 $L$ 表示序列长度，$d_{\text{model}}$ 表示隐藏层的维度。多头注意力机制将输入序列分别映射为 $h$ 个不同的查询（Query）、键（Key）和值（Value）序列，用于计算注意力分数。$Self-Attention$ 层的输入用矩阵 $X_i$ 进行表示，一般为词向量，则可以使用线性变换矩阵 $W^Q$，$W^K$，$W^V$用矩阵运算得到 $Q_i$，$K_i$，$V_i$。

$$a_i=W{x}_i$$
$$Q_i=W_{Q_i}{a}_i$$

$$K_i=W_{K_i}{a}_i$$

$$V_i=W_{V_i}{a}_i$$

每个注意力头都有自己的权重矩阵 $W_Q\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$、$W_K\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$ 和 $W_V\in {\mathbb{R}}^{d_{\text{model}}\times d_v}$，其中 $d_k$ 表示查询和键的维度，$d_v$ 表示值的维度。

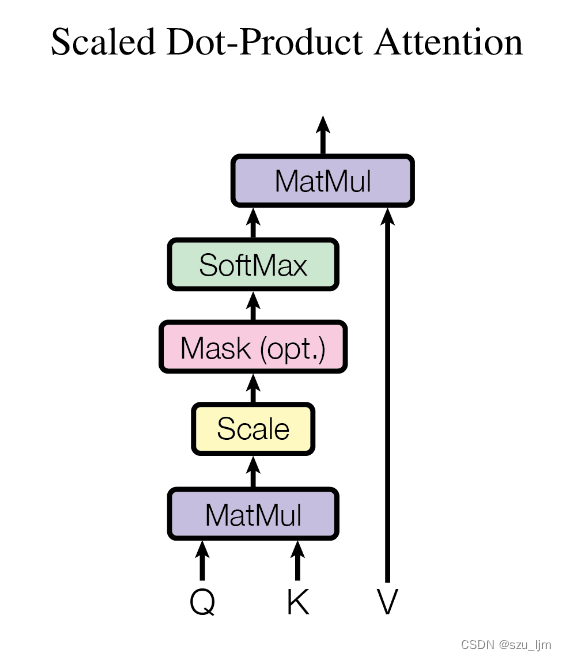
然后，针对每个注意力头，通过计算查询 $Q_i$、键 $K_i$ 和值 $V_i$ 的点积注意力得到注意力分数 $Attentio{n}_i$，其中$\sqrt{d_k}$ 是为了缩放注意力分数：

$$Attentio{n}_i=\text{softmax}\left(\frac{Q_i{K}_i^{\top }}{\sqrt{d_k}}\right)\cdot V_i$$

论文作者解释了自注意力机制的几个优势，一个是能减少计算的复杂度，并行计算序列输入会使模型训练更加高效，相比CNN和RNN这种串行计算效率更高。第二是能更加有效地建模长时序信息依赖关系，同时减少前向传播和反向传播在网络中的传播路径，提高网络参数的更新速率

2、多头注意力机制（Multi-Head Attention）

多头注意力机制允许模型同时关注输入序列中不同位置的信息，通过不同的权重矩阵学习不同的注意力表示。这有助于模型更好地捕捉序列中的关系和重要性，并提升模型的表示能力。将所有注意力头的输出拼接并经过线性变换，得到最终的多头注意力输出：

$$\text{MultiHead}(X)=\text{Concat}(A_1,A_2,\dots ,A_h)W_O$$

其中 $\text{Concat}$ 表示将所有注意力头的输出进行拼接，$W_O\in {\mathbb{R}}^{h{d}_v\times d_{\text{model}}}$ 是最终输出的线性变换权重矩阵。

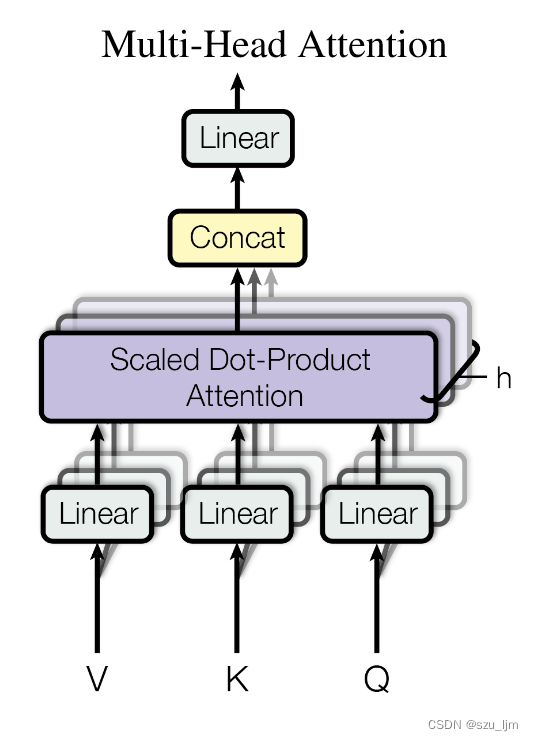
多头注意力机制跟人的注意力机制很像，比如我们在读一段很长的话时，我们有不同的注意力窗口，但其中有些则是更为重要的信息特征，多头注意力能让更多重要的信息特征关联起来，进行全局的信息补充和理解

3、位置编码（Positional Encoding）

在RNN（LSTM，GRU）中，时间步长的概念按顺序编码，因为输入/输出流一次一个。 对于Transformer，序列输入的时候是并行的，所以不能很好的衡量序列片段间的位置相关性，作者将时间编码为正弦波，作为附加的额外输入。 这样的信号被添加到输入和输出以表示时间的流逝。

$$\text{PE}(pos,2i)=\sin \left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$$

$$\text{PE}(pos,2i+1)=\cos \left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$$

$pos$ 是单词的位置，$d_{\text{model}}$是这个向量的维数。也就是说，PE的每一个维度对应一个正弦曲线。对于偶数(2i)我们使用正弦，对于奇数(2i + 1)我们使用余弦。通过这种方式，我们能够为输入序列的每个标记提供不同的编码，因此现在可以并行地传递输入。为什么用三角函数，为什么偶数维（2i）用sin，奇数维（2i+1）用cos？

由三角函数性质公式：
$$sin(\alpha +\beta )=sin\alpha cos\beta +cos\alpha sin\beta$$
$$cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta$$

代入上述公式有：
$$P{E}_{(M+N，2i)}=P{E}_{(M，2i)}\times P{E}_{(N，2i+1)}+P{E}_{(M，2i+1)\times PE(N，2i)}$$
$$P{E}_{(M+N，2i+1)}=P{E}_{(M，2i+1)}\times P{E}_{(N，2i+1)}-P{E}_{(M，2i)\times PE(N，2i)}$$

也就是说，$P{E}_{(M+N)}$ 可由 $P{E}_{(M)}$ 与 $P{E}_{(N)}$ 相互计算得到，即各个位置间可以相互计算得到，绝对位置编码中包含了相对位置的信息

二、Pytorch源码浅析

1. Attention

注意力层的思路就是，首先取Q矩阵最后一维的大小，将Q、K、V矩阵进行运算，除$\sqrt{d_k}$ 来缩放注意力分数，再用softmax归一化到[0, 1]，下面代码还做了剪枝和masked判断，用来降低模型参数复杂度

def attention(query, key, value, mask=None, dropout=None):

    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1))/math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn
1
2
3
4
5
6
7
8
9
10

2、MultiHeadedAttention

多头注意力集合多个Attention Layers，首先判断d-model%h是否有余数，如果有就报错，还有查看Q矩阵的第一维度size，决定后面attention映射计算和全连接层size。contiguous的作用是断掉拷贝之间的联系。forward函数最后又把矩阵转置回来，然后经过一层全连接最后返回出去。

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0                             
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)

        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2) for l, x in zip(self.linears, (query, key, value))]
        # 2) Apply attention on all the projected vectors in batch.
        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)

        # 3) "Concat" using a view and apply a final linear.
        x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
        return self.linears[-1](x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3、PositionalEncoding

PositionalEncoding是编码器位置向量的编码，首先根据权重矩阵维度构造PE列表，构造e指数函数和正余弦函数，register-buffer的作用是在内存中定一个常量方便写入和读出，像位置编码向量这种常用的共享向量。forward函数实现的就是字符embedding与位置embedding的加和

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
        return self.dropout(x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

4、Embeddings

torch中的nn.embedding做了一下拓展，按照权重矩阵维度进行嵌入

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)
1
2
3
4
5
6
7
8

5、LayerNormalization

归一化层就是标准化的计算公式，计算均值和方差进行归一化

class LayerNorm(nn.Module):
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2


class SublayerConnection(nn.Module):

    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        return x + self.dropout(sublayer(self.norm(x)))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

---

总结

以上就是Transformers网络学习笔记的全部内容，本文简单介绍了Transformers网络重要结构的数学原理以及简单分析一下Transformers的代码。Transformers 模型在自然语言处理（NLP）领域取得了巨大的成功，并在许多任务中取得了 state-of-the-art 的结果。后面研究人员也开始将其应用于计算机视觉（Computer Vision）领域，并取得了一些令人印象深刻的结果，像ViT（Vision Transformers）这种SOTA模型。