-
梯度下降法
梯度下降法
对于一个二元一次函数
y = ax + b,我们只需要知道两个(x,y)点即可获取到a、b的值,我们称其为精确解,如下图:
但是如果该函数中存在已知分布的噪声,那么又该如何求解:
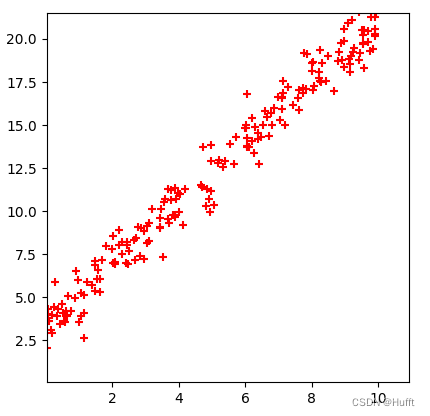
我们可以假设
a、b为任意值,则根据输入x有预测输出y',实际的y值与预测的y'的差距我们称为损失,对于已知的若干(x,y)点的损失则为损失函数:
l o s s = 1 n ∑ i = 1 n ( y i − y ′ i ) 2 loss = \frac{1}{n} \sum_{i=1}^n (y_i - {y'}_i)^2 loss=n1i=1∑n(yi−y′i)2我们最终的目的是求得
a、b使损失值最小,所以可以从当前的参数取值,一步步的按照损失函数下坡的方向下降,直到走到最低点。第一要保证 loss 是下降的,第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们:沿着梯度的反方向,是函数值下降最快的方向,所以只需要对损失函数求导,并且沿着导数的反方向逐步移动,则会找到最佳的a、b。我们称这种求解方法为梯度下降法,称该问题为线性回归问题。
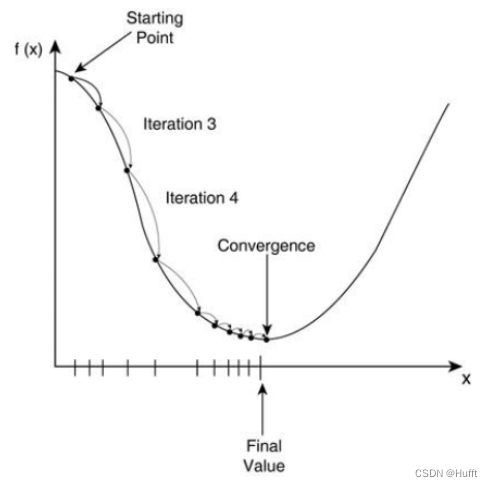
代码实现
对
a、b分别求偏导数:
l o s s = 1 n ∑ i = 1 n ( a x i + b − y i ) 2 loss = \frac{1}{n} \sum_{i=1}^n (ax_i + b - y_i)^2 loss=n1i=1∑n(axi+b−yi)2
∂ l o s s ∂ a = 2 n ∑ i = 1 n [ ( a x i + b − y i ) x i ] {\partial loss \over \partial a} = {2\over n}\sum_{i=1}^n [(ax_i+b-y_i)x_i] ∂a∂loss=n2i=1∑n[(axi+b−yi)xi]
∂ l o s s ∂ b = 2 n ∑ i = 1 n ( a x i + b − y i ) {\partial loss \over \partial b} = {2\over n}\sum_{i=1}^n (ax_i+b-y_i) ∂b∂loss=n2i=1∑n(axi+b−yi)# 线性回归模型 import numpy as np import matplotlib.pyplot as plt # 创建样本 y = ax+b,其中x = 1.72,b = 3.69 def create_sample(): # 生成 0-100 之间 200 个随机数 x = np.random.rand(200) * 10 y = x * 1.72 + 3.69 + (np.random.normal(size=200)) # 转换为 [[x1,y1],[x2,y2]...[xn,yn]] 的矩阵 return np.array(list(zip(x, y))) # 计算梯度,并更新 a,b 值 def gradient(a_cur, b_cur, points, learning_rate): a_gradient = 0 b_gradient = 0 points_length = len(points) # 计算梯度 for i in range(0, points_length): x = points[i, 0] y = points[i, 1] a_gradient += (2 / points_length) * x * (a_cur * x + b_cur - y) b_gradient += (2 / points_length) * (a_cur * x + b_cur - y) # 更新 a、b 值 new_a = a_cur - learning_rate * a_gradient new_b = b_cur - learning_rate * b_gradient return [new_a, new_b] # 计算损失 def computer_loss(a, b, points): points_length = len(points) loss = 0 for i in range(0, points_length): x = points[i, 0] y = points[i, 1] loss += (a * x + b - y) ** 2 loss /= points_length return loss points = create_sample() print("points", points) a = 0 b = 0 loss_list = list() for i in range(0, 100000): [a, b] = gradient(a, b, points, 0.001) loss_list.append(computer_loss(a, b, points)) #求得 a = 1.7219045715547612 b = 3.6145089870651086 print("a = {} b = {}".format(a, b)) # 绘制损失函数 plt.plot(loss_list) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
最终损失区域0
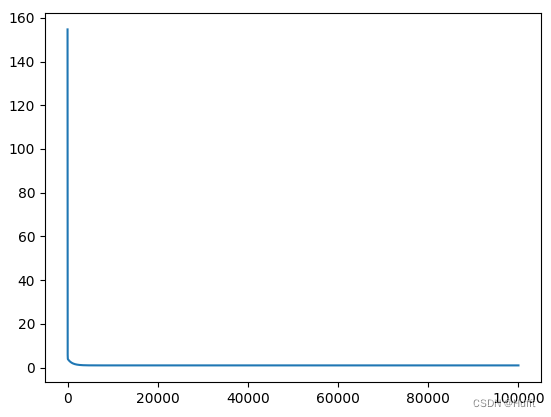
-
相关阅读:
[附源码]Python计算机毕业设计SSM健身房预约平台(程序+LW)
公路施工机械技术突破和创新后的实施影响
【笔者感悟】笔者的学习感悟【九】
MySQL高阶语句(一)
云原生SIEM解决方案
【GlobalMapper精品教程】063:线转面,面转线、线折点转点、面折点转点、点生成线、点生成面案例教程
Java异常03:自定义异常及经验小结
Java网络开发(Session)—— 从http请求 到 cookie 到 session & 用 session控制 删改数据的权限
每天一个数据分析题(三百九十七)- 逻辑回归
前端研习录(35)——ES6 对象解构赋值讲解及示例分析
- 原文地址:https://blog.csdn.net/stone_gentle/article/details/133099163
