-
博弈论——反应函数
反应函数
1 引言
谢老师的《经济博弈论》书中对反应函数并没有给出一般笼统的定义,而是将其应用与古诺模型并给出了相关解释:反应函数是指在无限策略的古诺博弈模型中,博弈方的策略有无限多种,因此各个博弈方的最佳对策也有无限种,它们之间往往构成一种连续函数的关系,把这个连续函数称为反应函数。
有趣的是百度百科对于反应函数的定义与谢老师书上的一致,但是在该词条正文中,还有一句话是:在经济学中,反应函数在博弈论古诺模型中有相应的应用,在假设竞争对手产生了给定产出水平的情况下,反应函数可以得出你的最佳产出水平。
这句话其实比较通俗易懂得解释了反应函数的定义,就是说:反应函数就是当一个企业做经营决策(如产量决策、价格决策等)时,对于给定的其他竞争企业的经营决策,所做出的反应,表明这一反应关系的函数。大白话就是,你做了决策后,我根据你的决策做出我的决策,那描述“根据你的决定,做出我的决定”的关系的函数,称为反应函数。2 反应函数
根据你的先手,决定对我最有利的后手,是反应函数最关键的地方。我们以前一篇文章的连续产量古诺模型为例:
在上述两寡头古诺模型中,对厂商2的任意产量q2 ,厂商1的最佳对策产量q1,是下面最大化问题的解:
m a x q 1 π 1 = m a x q 1 ( − q 1 2 − c q 1 − q 1 q 2 + 8 q 1 ) \underset{q_1}{max}π_1=\underset{q_1}{max}(-q_1^2-cq_1-q_1 q_2+8q_1) q1maxπ1=q1max(−q12−cq1−q1q2+8q1)
也就是给定 q 2 q_2 q2,求能让厂商1得到最优利润的 q 1 q_1 q1。令 π 1 π_1 π1对 q 1 q_1 q1求一阶导,并等于0,得到:
− 2 q 1 − c − q 2 + 8 = 0 -2q_1-c-q_2+8=0 −2q1−c−q2+8=0
即:
q 1 = 8 − c − q 2 2 q_1=\frac{8-c-q_2}{2} q1=28−c−q2
令:
q 1 = 8 − c − q 2 2 = R 1 ( q 2 ) q_1=\frac{8-c-q_2}{2}=R_1 (q_2) q1=28−c−q2=R1(q2)
得到的这个函数 R ( q 2 ) R(q_2) R(q2)是对于厂商2的每一个可能产量,厂商1最佳产量的计算公式。这个函数称为厂商1对厂商⒉产量的“反应函数”(reaction function)。
同理,可求出厂商2对厂商1产量 q 1 q1 q1的反应函数为:
q 2 = 8 − c − q 1 2 = R 2 ( q 1 ) q_2=\frac{8-c-q_1}{2}=R_2 (q_1) q2=28−c−q1=R2(q1)
显而易见, R 1 ( q 2 ) R_1 (q_2) R1(q2)、 R 2 ( q 1 ) R_2 (q_1) R2(q1)这两个反应函数都是线性函数(linear function),我们在坐标平面上用两条直线表示出来,更好得进行研究。3 图像
首先我们分别确定两个线性函数在坐标系上的两点,以数对 ( q 1 , q 2 ) (q_1,q_2) (q1,q2)表示。对于 q 1 = R 1 ( q 2 ) q_1=R_1 (q_2) q1=R1(q2),其经过 ( 8 − c 2 , 0 ) (\frac{8-c}{2},0) (28−c,0)、 ( 0 , 8 − c ) (0,8-c) (0,8−c)两点;对于 q 2 = R 2 ( q 1 ) q_2=R_2 (q_1) q2=R2(q1),其经过 ( 8 − c , 0 ) (8-c,0) (8−c,0)、 ( 0 , 8 − c 2 ) (0,\frac{8-c}{2}) (0,28−c)两点,如下图所示:
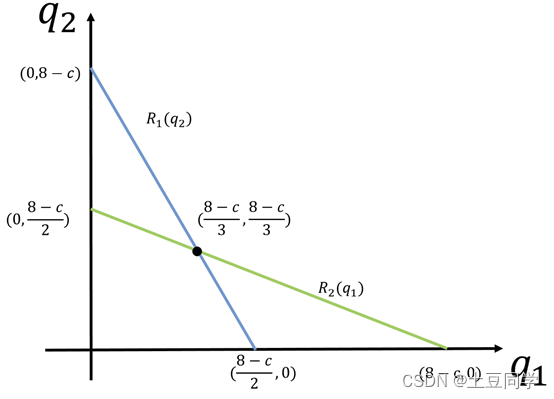
根据图像可以看出:
- 当一方产量选择为0时,另一方的最佳反应为 8 − c 2 \frac{8-c}{2} 28−c,这正是上篇文章中提到的实现市场总利益最大的产量,这时候等于一个厂商垄断市场;
- 当一方产量达到 8 − c 8-c 8−c时,另一方被迫生产0,因为后者坚持生产无利可图.
在两个反应函数对应的两条直线上,只有交点 ( 8 − c 3 , 8 − c 3 ) (\frac{8-c}{3},\frac{8-c}{3}) (38−c,38−c)代表的产量组合,才是由相互对对方的最佳反应构成的。
需要注意的是, q 1 = R 1 ( q 2 ) q_1=R_1 (q_2) q1=R1(q2)上其他所有点 ( q 1 , q 2 ) (q_1,q_2) (q1,q2)代表了只有 q 1 q_1 q1是对 q 2 q_2 q2的最佳反应, q 2 q_2 q2不是对 q 1 q_1 q1的最佳反应;而 q 2 = R 2 ( q 1 ) q_2=R_2 (q_1) q2=R2(q1)上其他点代表了只有 q 2 q_2 q2是对 q 1 q_1 q1的最佳反应, q 1 q_1 q1不是对 q 2 q_2 q2的最佳反应。因此,根据纳什均衡的定义,当 ( q 1 , q 2 ) = ( 8 − c 3 , 8 − c 3 ) (q_1,q_2)=(\frac{8-c}{3},\frac{8-c}{3}) (q1,q2)=(38−c,38−c),即 q 1 q_1 q1、 q 2 q_2 q2相互是对于对方的最佳反应,是该博弈唯一的纳什均衡。这与上篇文章通过数理推导得到的结论一致。4 结语
得益是策略多元连续函数的博弈,都可以求每个博弈方的反应函数,解出各博弈方反应函数的交点就是纳什均衡。这种用反应函数求纳什均衡的方法,称为“反应函数法”。
反应函数法是分析一般具有无限多种策略、连续策略空间博弈问题的基本方法,但并不是说反应函数可以解决一切有无限策略、连续策略空间的博弈。因为在有些博弈中,得益函数不是可微函数,无法用先求导数找各个博弈方的反应函数,再解联立方程组的方法求纳什均衡。而且即使得益函数可以求导,可以求出各个博弈方的反应函数,也并不意味着一定能找到均衡结果。因为在有些博弈问题中,博弈方的得益函数比较复杂,各自的反应函数也比较复杂,并不能够保证反应函数有交点,也不能保证有唯一交点。 -
相关阅读:
C_平均数_猴子吃桃问题
java计算机毕业设计健身俱乐部管理系统MyBatis+系统+LW文档+源码+调试部署
<HarmonyOS第一课>运行Hello World——闯关习题及答案
自定义注解
彻底搞懂Mybatis
Spark安装教程
vue学习笔记——简单入门总结(二)
ES性能优化最佳实践- 检索性能提升30倍!
项目管理VS项目治理,初级项目经理的你肯定弄混过
【python入门篇】条件表达式、循环(5)
- 原文地址:https://blog.csdn.net/qq_43403025/article/details/133251749