HJ65 查找两个字符串a,b中的最长公共子串

题目：

HJ65 查找两个字符串a,b中的最长公共子串

题解：

一、暴力枚举

1. 枚举求出较短串的所有子串
2. 遍历所有子串，判断长串是否包含子串
3. 记录最长子串

    private String getMaxSubString2(String s1, String s2) {
        String longgerString = s1.length() > s2.length() ? s1 : s2;
        String shorterString = s1.length() > s2.length() ? s2 : s1;
 
        char[] chars1 = shorterString.toCharArray();
        List subStringSet = new ArrayList<>();
        for (int i = 0; i < chars1.length; i++) {
            for (int j = i+1; j <= chars1.length; j++) {
                subStringSet.add(shorterString.substring(i, j));
            }
 
        }
 
        String result = "";
        for (String s : subStringSet) {
            if (longgerString.contains(s) && s.length() > result.length()) {
                result = s;
            }
        }
 
        return result;
    }

时间复杂度：O()

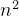二、滑动窗口

1. 遍历段串，每个字符作为子串起始字符
2. 从长串中找到对应字符，依次向后遍历
3. 记录相同子串长度，遇到字符不相等就枚举下个字符作为起始字符

private String getMaxSubString(String s1, String s2) {
        if (s1.length() > s2.length()) {
            String temp = s1;
            s1 = s2;
            s2 = temp;
        }
 
        char[] chars1 = s1.toCharArray();
        char[] chars2 = s2.toCharArray();
 
        String result = "";
        for (int i = 0; i < chars1.length; i++) {
            char char1 = chars1[i];
            for (int j = 0; j < chars2.length; j++) {
                char char2 = chars2[j];
                if (char1 != char2) {
                    continue;
                }
 
                int index1 = i;
                int index2 = j;
                while (index1 < chars1.length && index2 < chars2.length && chars1[index1] == chars2[index2]) {
                    index1++;
                    index2++;
                }
 
                String substring = s1.substring(i, index1);
                if (substring.length() > result.length()) {
                    result = substring;
                }
            }
        }
 
        return result;
    }

时间复杂度：O(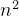*m)

三、动态规划

设dp[i][j]表示 s1 位置 i 与 s2 位置 j 之间最长子串长度，那么可得dp方程：

1. dp[i][j] = dp[i-1][j-1] + 1 (s1[i-1] == s2[j-1])
2. dp[i][j] = 0 (s1[i-1] != s2[j-1])

private String getMaxSubStringForDP(String s1, String s2) {
        if (s1.length() > s2.length()) {
            String temp = s1;
            s1 = s2;
            s2 = temp;
        }
 
        char[] chars1 = s1.toCharArray();
        char[] chars2 = s2.toCharArray();
        int len1 = chars1.length;
        int len2 = chars2.length;
 
        int[][] dp = new int[len1+1][len2+1];
        int maxLength = 0;
        int index = 0;
        for(int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (chars1[i-1] == chars2[j-1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                    if (dp[i][j] > maxLength) {
                        maxLength = dp[i][j];
                        index = i;
                    }
                }
            }
        }
 
        return s1.substring(index-maxLength, index);
    }

时间复杂度：O(n*m)