【国科大卜算】Radar Installation

Radar Installation

Problem description

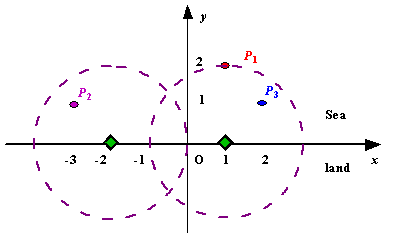
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.

The input is terminated by a line containing pair of zeros

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. “-1” installation means no solution for that case.

Sample

My understand

以海岛为圆心画圆

• 若为相交与x轴上，则无法安装雷达
• 若相交与x轴上，则求其交点，并对其进行排序操作，其次序按照由左交点从小到大，排序，若出现一次重合率最大的段，则+1

#include 
#include 
#include 

using namespace std;

struct point {
    double left;
    double right;
};

bool operator<(point p1, point p2) {
    return p1.left < p2.left;
}

int main() {
    int n, d, c = 0;
    point p[2010] = {};
    while (cin >> n >> d && (n != 0 && d != 0)) {
        int x, y, flag = 0, t = 0;
        for (int i = 0; i < n; ++i) {
            cin >> x >> y;
            if (d < fabs(y)) {
                flag = 1;
            } else {
                p[t].left = x - sqrt(d * d - y * y);
                p[t].right = x + sqrt(d * d - y * y);
                t++;
            }
        }
        if (flag) {
            cout << "Case " << ++c << ": -1" << endl;
        } else {
            sort(p, p + t);
            point temp = p[0];
            int m = 1;
            for (int i = 1; i < t; ++i) {
                if (p[i].left > temp.right) {
                    m++;
                    temp = p[i];
                } else if (p[i].right < temp.right) {
                    temp = p[i];
                }
            }
            cout << "Case " << ++c << ": " << m << endl;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48