【数据结构】二叉树的前序遍历（七）

 题目：二叉树的前序遍历

题目详情：给你二叉树的根节点 root ，返回它节点值的 前序 遍历；

我们先来看几个示例：

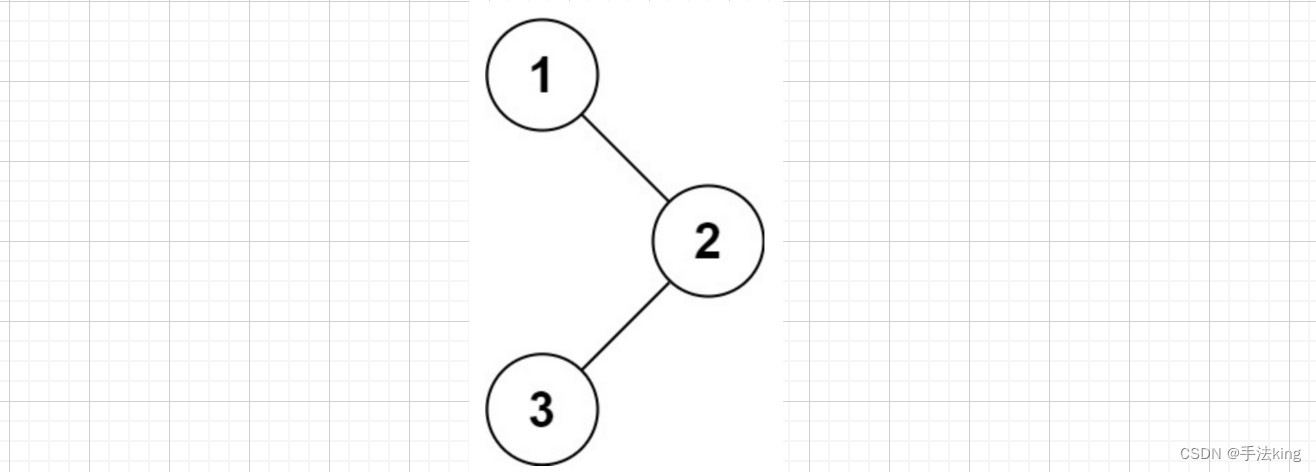
输入：root = [ 1，null，2，3 ]

输出：[ 1，2，3 ]

 示例2：

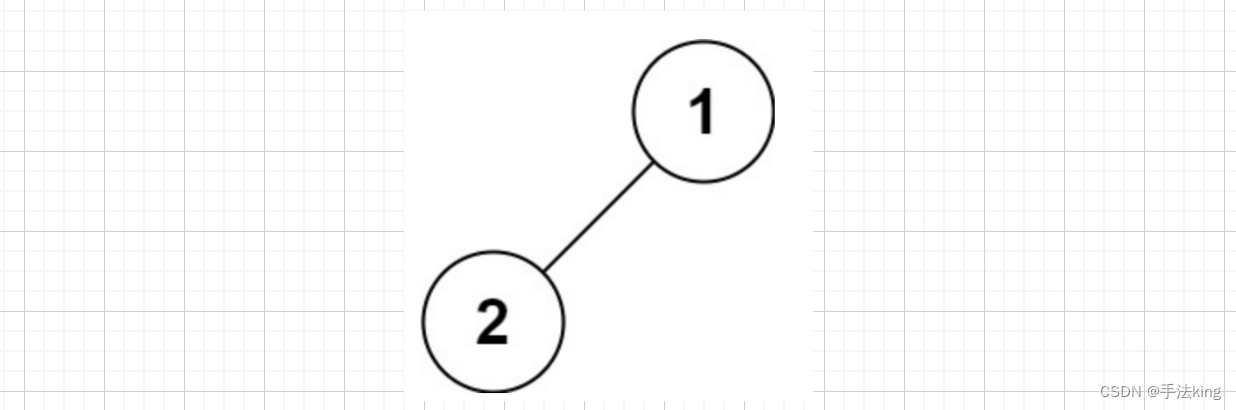
输入：root = [ 1，2 ]

输出：[ 1，2 ]

示例三：

输入：root = [  ]

输出：[  ]

提示：

树中结点数目在范围【0，100】内

-100 <= Node.val <= 100

开始分析：

通过以上的示例我们得知，这道题呢就是把一棵树用前序遍历的方式将结点的值赋给一个数组，然后返回这个数组的指针；

我们之前学过二叉树的前序遍历打印结点的值，现在是将结点的值储存起来，其实原理都一样；

这个是要实现的函数的基本信息；

int* preorderTraversal(struct TreeNode* root, int* returnSize)

思路实现：

我们首先要确定数组的大小，数组的个数等于树中结点的个数，所以我们要先计算树中结点的个数；

int TreeSize(struct TreeNode* root)
{
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}   
//算结点的个数
*returnSize=TreeSize(root);

这个计算树结点个数的函数之前有些过，大体思路就是树结点的总和等于 根结点本身加上左，右子树的结点个数；

然后数组的元素个数知道了就要开始申请动态空间来定义数组了；

//开辟动态空间
int* arr=(int*)malloc(sizeof(int)*(*returnSize));

直接一个 malloc 拿下，元素类型与树结点的值类型一致；

然后数组也有了我们就要对其赋值了；

易错点：

1，前序遍历是需要用递归来实现的，不能直接在主函数里递归，因为主函数里有开辟动态空间还挺大的，会造成堆溢出，所以我们需要用另外一个函数来进行赋值操作；

void _preorderTraversal(struct TreeNode* root,int* arr)
 {
     if(root==NULL)
     {
         return ;
     }
     int i=0;
     arr[i++]=root->val;
     _preorderTraversal(root->left,arr);
     _preorderTraversal(root->right,arr);
 } 
  
    //赋值
     _preorderTraversal(root,arr);

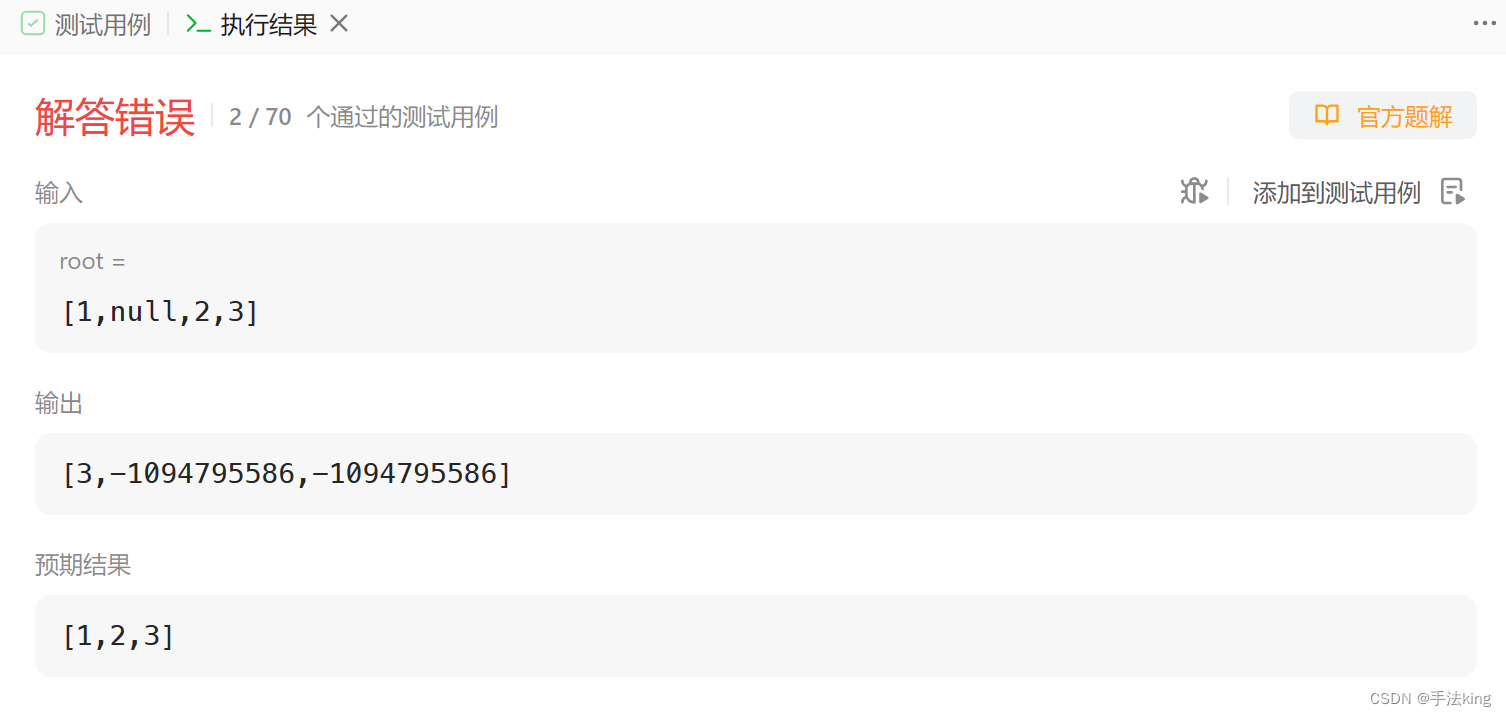
初学者们经常犯的错误，这里很明显错误的是下标 i 在递归调用函数时的不断重置，那我们把下标 i 放在主函数里是不是就可以解决呢？

void _preorderTraversal(struct TreeNode* root,int* arr,int i)
 {
     if(root==NULL)
     {
         return ;
     }
     arr[i++]=root->val;
     _preorderTraversal(root->left,arr,i);
     _preorderTraversal(root->right,arr,i);
 }   
int i=0;
//赋值
_preorderTraversal(root,arr,i);

这为什么也通过不了呢？很简单，每一次调用的下标 i 只是上一个函数的形参而已，形参的改变不会影响实参！

这有人就会问呀那也运行成功了一半呀！ 那是因为能运行成功的树都是【斜树】这种树都只有一边的，我前面也介绍过；

斜树图示：

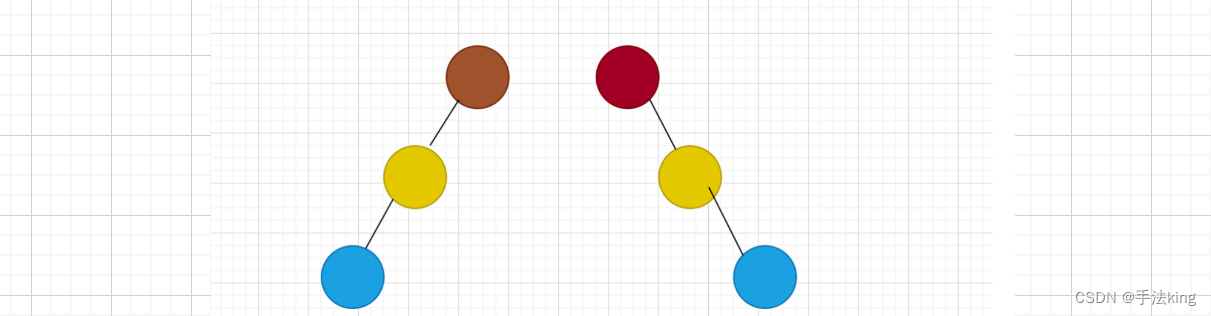
对，就是这种树才程序才可以通过，那为什么其他树不可以呢？因为像【斜树】这种每次的函数返回都是空并不涉及下标 i 的值的改变，但是其他树呢，就比如这棵树；

当函数走到 D 点的时候下标 i 为3，然后返回 B 开始给其右子树 E 赋值；

此时 E 中下标 i 的值是 4 吗？并不是！ D 中改变 i 的值出了函数就失效了，形参的改变不能影响实参，所以此时 E 中下标 i 的值还是 2 ，因此程序通过不了了；

所以既然传值不行，那我们就传地址嘛，这样下标 i 就可以灵活变通了；

void _preorderTraversal(struct TreeNode* root,int* arr,int* i)
 {
     if(root==NULL)
     {
         return ;
     }
     arr[(*i)++]=root->val;
     _preorderTraversal(root->left,arr,i);
     _preorderTraversal(root->right,arr,i);
 }  
 
 int i=0;
 //赋值
  _preorderTraversal(root,arr,&i);

这样就ok了，还有人说用全局变量也行，那我们来看看；

int i=0;
void _preorderTraversal(struct TreeNode* root,int* arr)
 {
     if(root==NULL)
     {
         return ;
     }
     arr[i++]=root->val;
     _preorderTraversal(root->left,arr);
     _preorderTraversal(root->right,arr);
 }    
 
//赋值
 _preorderTraversal(root,arr);

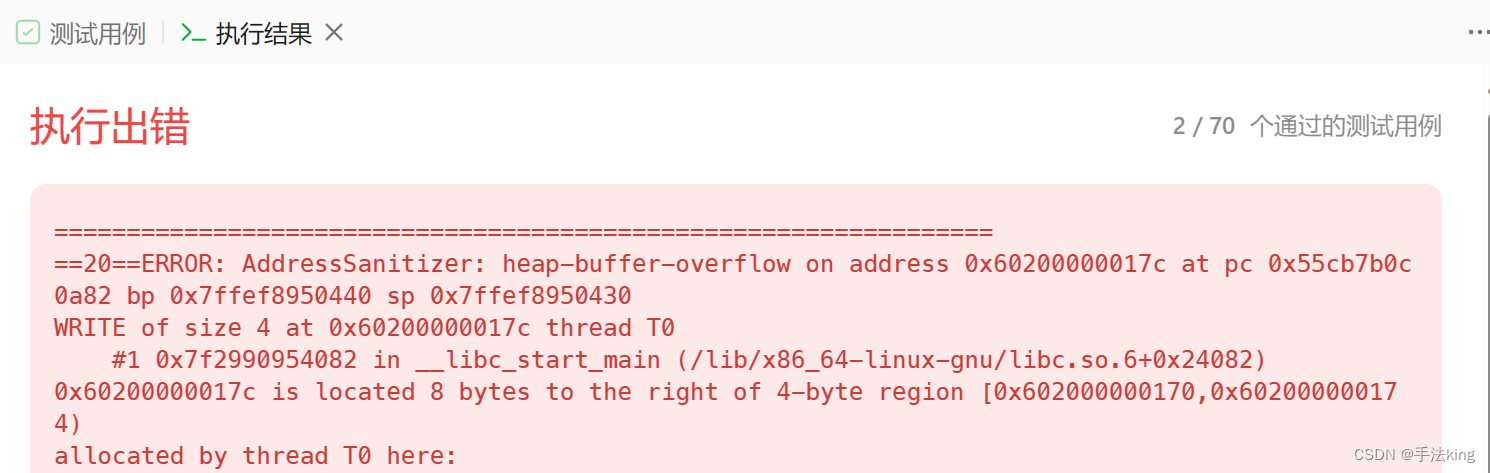
大家忽略了一个问题，这种方式只能是一次性的；

因为全局变量 i 的值会一直变化且保存的，而要通过的话是要进行大量测试的，要调用很多次函数，而每一次调用函数下标 i 的值都是在上个函数里调用过的值，并没有重置，所以调用多了下标 i 就会无限大就会越界访问了；

源代码：

void _preorderTraversal(struct TreeNode* root,int* arr,int* i)
 {
     if(root==NULL)
     {
         return ;
     }
     arr[(*i)++]=root->val;
     _preorderTraversal(root->left,arr,i);
     _preorderTraversal(root->right,arr,i);
 }
 
int TreeSize(struct TreeNode* root)
{
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
 
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    //算结点的个数
    *returnSize=TreeSize(root);
    //开辟动态空间
    int* arr=(int*)malloc(sizeof(int)*(*returnSize));
    int i=0;
    //赋值
     _preorderTraversal(root,arr,&i);
     return arr;
}

这就是这道题的解题思路以及易错点了，写程序还是得细心得全面，特别是递归问题考虑的东西就更多了；

这阶段也还是带大家刷一些常见且经典的题目，掌握算法形成思路！

后面博主会陆续更新；

如有不足之处欢迎来补充交流！

完结。

---