• 哈希(hash)——【C++实现】

    在这里插入图片描述

    本章gitee代码仓库：Hash

    文章目录

    💐1. 哈希概念

    我们对元素进行搜索有几种方式：

    1. 暴力查找，直接遍历元素，时间复杂度为O(N)

      image-20230917101056152

    2. 二分查找，时间复杂度为O(logN)

      但二分查找有2个弊端：

      • 必须为有序
      • 增删查改不方便

      这两个弊端导致二分查找只是一个理想的查找方式，并不是很现实

      image-20230917101700713

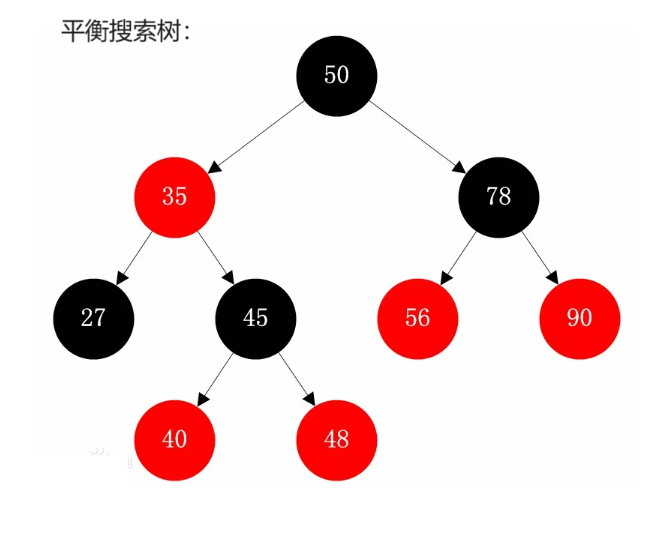
    3. 平衡搜索树，增删查改的时间复杂度都是O(logN)，总体性能都很不错

      image-20230917101710006

    这些结构中的元素关键码和存储位置都没有对应的关系，而有一种方法名为哈希（也叫散列），它提供了一种与这些完全不同的存储和查找方式，即将存储的值和存储的位置建立出一个对应的函数关系。

    有一种排序名为计数排序，将不同的值映射到对应的位置，这本质上就是哈希

    不了解的可以看下这篇文章——非比较排序——计数排序

    我们的通讯录，按照名字的首字母进行分类，本质也是哈希

    image-20230917103230972

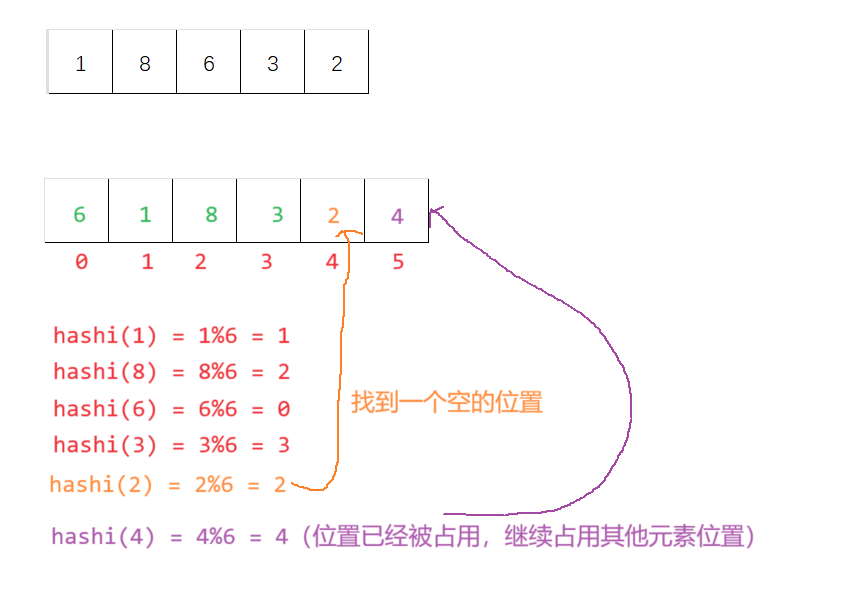
    以数组{1,8,6,3}为例，假设hashi = key % 6 ，那则有如下对应关系

    image-20230917104706750

    这样就能通过取模直接定位到该元素的位置

    但是如果进行插入元素，例如插入2，2%6=2，这就会导致和8的位置一样

    🌻2. 哈希冲突

    不同的关键字通过哈希函数计算出了相同的地址，值和位置出现了多对一的关系，这种线性称之为哈希冲突（哈希碰撞）。

    解决方案：

    1. 选择合理的哈希函数
    2. 拟定冲突方案

    🌼3. 哈希函数

    出现哈希碰撞的原因之一可能就是哈希函数设计的不合理

    🌸3.1 哈希函数设计原则

    • 哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域必须是[0,m-1]之间
    • 哈希函数计算出来的地址能均匀分布在整个空间中
    • 哈希函数较为简单，能在较短时间内计算出结构

    🌸3.2 常见哈希函数

    1. 直接定址法（值的范围集中）

      取某个线性函数作为散列的地址：Hash(key) = A*key + B

    2. 除留余数法（值的范围分散）

      设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，

      按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址

    🪴4. 哈希冲突解决方案

    🌱4.1 闭散列——开放定址法

    如果当前位置被占用，按照规则找到下一个位置（占用其他元素的位置）

    image-20230917112017514

    我们删除元素通常都不是直接删除，而采用覆盖的方式，而这里无法很好的覆盖

    例如我们删除元素1，如果挪动后面的数据，这就导致映射关系全部乱了，如果不直接覆盖，那么之后又元素插入进来的时候，1这个位置还是有元素的，无法插入

    所有这里采用状态的方式进行标记：

    • 存在——EXIST
    • 空——EMPTY
    • 删除——DELETE
    🌿4.11 负载因子

    哈希表定义了一个载荷因子：α = 填入表中元素个数 / 哈希表的长度，这个是表示哈希表装满长度的标志因子

    如果负载因子设计的大，那么哈希冲突的概率就越大（空间利用率高）

    如果负载因子设计的小，那么哈希冲突的概率就越小（空间利用率低）

    对于开放定址法，经过测算，负载因子应该控制在0.7 ~ 0.8，下面代码实现采用0.7

    🌿4.12 字符串哈希算法

    面对字符串的哈希函数，我们采用BKDRHash函数

    有兴趣可查看此篇文章——各种字符串Hash函数

    🌿4.13 代码实现
    template<class K>
struct DefaultHashFunc
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};
//模板特化
template<>
struct DefaultHashFunc<string>
{
	size_t operator()(const string& str)
	{
		//BKDR hash
		size_t hash = 0;
		for (auto ch : str)
		{
			hash *= 131;
			hash += ch;
		}
		return (size_t)str[0];
	}
};


//开放定址法
namespace open_address
{
	enum STATE
	{
		EXIST,
		EMPTY,
		DELETE
	};

	template<class K, class V>
	struct HashDate
	{
		pair<K, V> _kv;
		STATE _state = EMPTY;
	};

	template<class K, class V, class HashFunc = DefaultHashFunc<K>>
	class HashTable
	{
	public:
		HashTable()
		{
			_table.resize(10);	//预先开好10个空间
		}

		bool Insert(const pair<K, V>& kv)
		{

			if (Find(kv.first))
				return false;

			//扩容
			if (_n * 10 / _table.size() >= 7)	//设负载因子为0.7
			{
				size_t newSize = _table.size() * 2;
				//扩容之后关系改变，需要重新映射
				HashTable<K, V> newHT;
				newHT._table.resize(newSize);

				//旧表数据插入到新标
				for (size_t i = 0; i < _table.size(); i++)
				{
					if (_table[i]._state == EXIST)
					{
						newHT.Insert(_table[i]._kv);
					}
				}
				//新标和旧表交换
				_table.swap(newHT._table);
			}

			//不能取模capacity，虽然空间有，但访问还是要看size的大小，不然会发生越界
			HashFunc hf;
			size_t hashi = hf(kv.first) % _table.size();
			while (_table[hashi]._state == EXIST)
			{
				//线性探测
				hashi++;
				hashi %= _table.size();
			}
			_table[hashi]._kv = kv;
			_table[hashi]._state = EXIST;
			++_n;
			return true;
		}

		HashDate<const K, V>* Find(const K& key)
		{
			HashFunc hf;
			size_t hashi = hf(key) % _table.size();
			while (_table[hashi]._state != EMPTY)
			{
				if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
				{
					return (HashDate<const K, V>*) & _table[hashi];
				}
				++hashi;
				hashi %= _table.size();
			}
			return nullptr;
		}

		bool Erase(const K& key)
		{
			HashDate<const K, V>* ret = Find(key);
			if (ret)
			{
				ret->_state = DELETE;
				--_n;
				return true;
			}
			return false;
		}

	private:
		vector<HashDate<K, V>> _table;	//哈希表
		size_t _n = 0;	//有效元素个数
	};
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126

    线性探测会导致一片拥堵，为此还有一种方法为二次探测

    例如线性探测是：

    hashi = key % n;
//如果有值了 i>=0
hashi+=i;

    • 1
    • 2
    • 3

    而二次探测则是：

    hashi = key % n;
//如果有值 i>=0
hashi + i^2;

    • 1
    • 2
    • 3

    这样就能在一定程度上减少拥堵

    🌱4.2 开散列——哈希桶

    开放定址法的缺陷就是冲突会相互影响。而哈希桶的做法是，设置一个指针数组，如果发现冲突，则内部消化

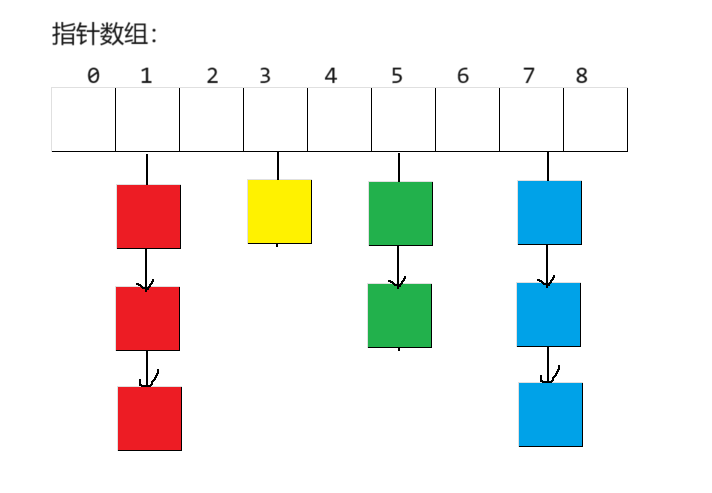
    image-20230917141822713

    这里桶的结构其实就是链式结构，对每个桶的管理就相当于对于链表的管理，下面的代码采用的是单链表

    这里也是需要进行扩容，如果不扩容，就会导致在某种情况下，桶越来越长，这样查找数据就变成了对链表数据的查找，时间复杂度为O(N)，所以还是需要进行扩容。

    这里的负载因子可以适当放大一点，一般负载因子控制在1，平均下来每个桶都有数据

    🌿4.21 代码实现

    这里的桶因为是自定义的链式结构，所以需要我们自己写拷贝构造和析构函数

    //哈希桶
namespace hash_bucket
{
	template<class K, class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K,V>* _next;

		HashNode(const pair<K, V>& kv)
			:_kv(kv)
			,_next(nullptr)
		{}
	};
	
	template<class K,class V,class HashFunc = DefaultHashFunc<K>>
	class HashTable
	{
		typedef HashNode<K, V> Node;

	public:
		HashTable()
		{
			_table.resize(10, nullptr);
		}

		~HashTable()
		{
			for (size_t i = 0; i <_table.size(); i++)
			{
				Node* cur = _table[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_table[i] = nullptr;
			}
		}
		//拷贝构造
		HashTable(const HashTable& ht)
		{
			_table.resize(ht._table.size(), nullptr);
			HashFunc hf;
			for (size_t i = 0; i < ht._table.size(); i++)
			{
				Node* cur = ht._table[i];
				while (cur)
				{
					Node* newNode = new Node(cur->_kv);
					size_t hashi = hf(cur->_kv.first) % ht._table.size();

					//头插
					newNode->_next = _table[hashi];
					_table[hashi] = newNode;

					cur = cur->_next;
				}
			}
			_n = ht._n;
		}

		void Print()
		{
			for (size_t i = 0; i < _table.size(); i++)
			{
				printf("[%d]->", (int)i);
				Node* cur = _table[i];
				while (cur)
				{
					cout << cur->_kv.first << "->";
					cur = cur->_next;
				}
				cout << "NULL" << endl;
			}
			cout << endl;
		}

		bool Insert(const pair<K, V>& kv)
		{
			if (Find(kv.first))
				return false;

			HashFunc hf;
			//扩容 -- 扩容的时候会稍微慢一点 ---^(扩容)-----^(扩容)----------^(扩容)-----.....
			//这里的扩容不能和开放定址法一样采用将旧表元素重新插入新表
			//因为这里涉及到开节点，新表开新节点，旧表释放旧节点，浪费
			if (_n == _table.size())
			{
				size_t newSize = _table.size() * 2;
				vector<Node*> newTable;
				newTable.resize(newSize,nullptr);

				//遍历旧表，将节点牵过来
				for (size_t i = 0; i < _table.size(); i++)
				{
					Node* cur = _table[i];
					while (cur)
					{
						Node* next = cur->_next;
						//头插到新表
						size_t newHashi = hf(cur->_kv.first) % newSize;
						cur->_next = newTable[newHashi];
						newTable[newHashi] = cur;

						cur = next;
					}
					_table[i] = nullptr;
				}
				_table.swap(newTable);
			}

			size_t hashi = hf(kv.first) % _table.size();
			//头插
			Node* newNode = new Node(kv);
			newNode->_next = _table[hashi];
			_table[hashi] = newNode;

			++_n;
			return true;
		}

		Node* Find(const K& key)
		{
			HashFunc hf;
			size_t hashi = hf(key) % _table.size();
			Node* cur = _table[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}
				cur = cur->_next;
			}
			return nullptr;
		}

		bool Erase(const K& key)
		{
			HashFunc hf;
			size_t hashi = hf(key) % _table.size();
			Node* prev = nullptr;
			Node* cur = _table[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					//头删
					if (prev == nullptr)
					{
						_table[hashi] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					--_n;
					delete cur;
					return true;
				}
				prev = cur;
				cur = cur->_next;
			}
			return false;
		}


	private:
		vector<Node*> _table;	//指针数组
		size_t _n = 0;	//有效元素
	};
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    • 168
    • 169
    • 170
    • 171
    • 172
    • 173
    • 174

    本次参考了《数据结构（用面向对象方法与C++语言描述）》，详细的内容可以参考此书

    那么本期的分享就到这里咯，我们下期再见，如果还有下期的话。

  • 相关阅读:
    词法分析基础
    常用的6款Go语言Web框架
    深入理解 python 虚拟机：令人拍案叫绝的字节码设计
    （附源码）ssm跨平台教学系统 毕业设计 280843
    运筹说 第76期 | 最短路问题
    APP自动化之weditor工具
    计算机毕业设计选什么题目好？springboot智慧养老中心管理系统
    【文章转载】Lance Martin的关于RAG的笔记
    Linux Netfilter框架之conntrack连接跟踪机制
    Pytest UI自动化测试实战实例
  • 原文地址：https://blog.csdn.net/Dirty_artist/article/details/133019231