-
【算法导论】堆排序
目录
2.4 以 A[1....n] 为堆的C语言MAX-HEAPIFY函数代码
1. 堆
1.1 堆的概念
堆是一个数组,它可以被看成一个近似的完全二叉树,树上的每一个节点对应数组中的一个元素。(堆也是一种存储结构,但这里讲的不是)
逻辑结构:

物理结构:

1.2 堆的分类
堆又可以分为:
- 大根堆: 父节点比子节点的值要大,A [PARENT( i )] ≥ A[ i ]
- 小根堆: 父节点比子节点的值要小,A [PARENT( i )] ≤ A[ i ]
1.3 堆的性质
1. 若存储堆的数组为A[1......n]则已知某节点 i 可求得其父节点为 ⌊i / 2⌋,左儿子节点为 2i,右儿子节点为 2i + 1.
2. 若存储堆的数组为A[0......n-1]则已知某节点 i 可求得其父节点为 ⌊(i-1) / 2⌋,左儿子节点为 2i+1,右儿子节点为 2i + 2.
1.4 堆的高度
在算法书中定义的堆的高度为:堆中某一结点的高度为该节点到叶节点最长简单路径上边的数目。
在数据结构书中定义堆的高度:从叶节点那一层到该节点所在层的层数。(比算法书定义的高度多1)
2. 维护堆的性质
2.1 大根堆的维护过程示意图
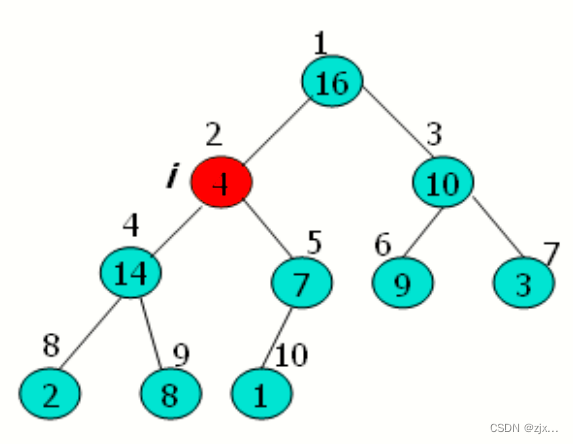
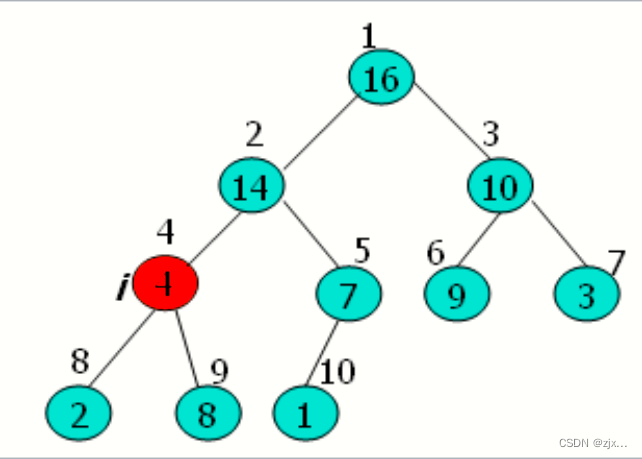

2.2 大根堆的维护思路
1. 维护大根堆性质的函数为MAX-HEAPIFY,在程序每一步中,从A [ i ]、A [ LEFT( i ) ]、A [RIGHT( i )]中选出最大的,并将其下标存储在largest中。
2. 如果A [ i ]是最大的,那么以 i 为根节点的子树已经是最大堆,程序结束。
3. 否则最大元素是 i 的某个孩子节点,则交换 A[ i ] 与 A [ largest ] 的值。从而使 i 及其孩子都满足大根堆的性质。
4. 在交换后,下标 largest 的结点的值是原来的 A [ i ],于是以该节点为根的字数又有可能违反大根堆性质。因此需要对该子树递归调用 MAX-HEAPIFY.
2.3 MAX-HEAPIFY函数伪代码
- MAX-HEAPIFY(A,i)
- l = LEFT(i) // 取该节点的左儿子节点
- r = RIGHT(i) // 取该节点的右儿子节点
- if l<=A.heap-size and A[l] > A[i]
- largest = l
- else
- largest = i
- if r<=A.heap-size and A[r] > A[largest]
- largest = r
- if largest ! = i
- exchange A[i] with A[largest]
- MAX-HEAPIFY(A,largest)
2.4 以 A[1....n] 为堆的C语言MAX-HEAPIFY函数代码
- void MAX_HEAPIFY(int A[], int i,int heap_size)
- {
- int l = i * 2;
- int r = i * 2 + 1;
- int largest = 0;
- if (l <= heap_size && A[l] > A[i])
- {
- largest = l;
- }
- else {
- largest = i;
- }
- if (r <= heap_size && A[r] > A[largest])
- {
- largest = r;
- }
- if (largest != i)
- {
- swap(A[i], A[largest]);
- MAX_HEAPIFY(A, largest, heap_size);
- }
- }
时间复杂度:O (h),其中 h 为树的高度。
3. 建堆
3.1 建堆思路
只需要找到最后一个有子节点的节点(T),然后从该节点到根节点逆向调用MAX_HEAPIFY函数即可。
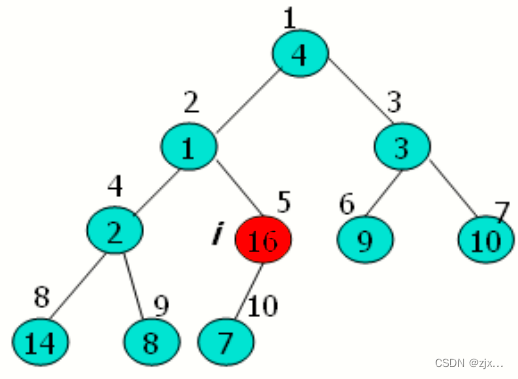
如上图所示,T节点即为元素值为16 的 5 号节点,然后遍历 4->3->2->->1 号节点执行MAX_HEAPIFY。
3.2 寻找最后一个父节点
二叉树的度(出度),就是该点所拥有的孩子数。可以分为 n0、n1、n2.
入度数(边数)= n0 + n1 + n2 − 1
出度数(边数)= 0∗n0 + 1∗n1 + 2∗n2
以上两式联立可得 n0 = n2 + 1 ---> n2 = n0 -1
总的节点数 n = n0 + n1 + n2,将 n2 = n0 -1 带入上式可得 n = n0 + n1 + n0 -1 = 2*n0 + n1 - 1
由此推得:
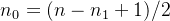
由于 n1 的数量等于1或0,所以 n0 = ⌈n / 2⌉,最后一个父节点的数量为 n - n0,综上可以得到最后一个父节点的下标为:⌊n / 2⌋
3.3 建堆算法
伪代码:
- BUILD-MAX-HEAP(A)
- Heap-size[A] ← Length[A]
- for i = ⌊Length[A]/2⌋ downto 1
- doMAX-HEAPIFY(A, i)
C 语言代码:
- void BUILD_MAX_HEAP(int A[],int A_length)
- {
- int heap_size = A_length;
- for (int i = A_length / 2; i >= 1; i--)
- {
- MAX_HEAPIFY(A, i, heap_size);
- }
- }
建堆所用时间:

3.4 建堆过程图示
以以下A数组为例:

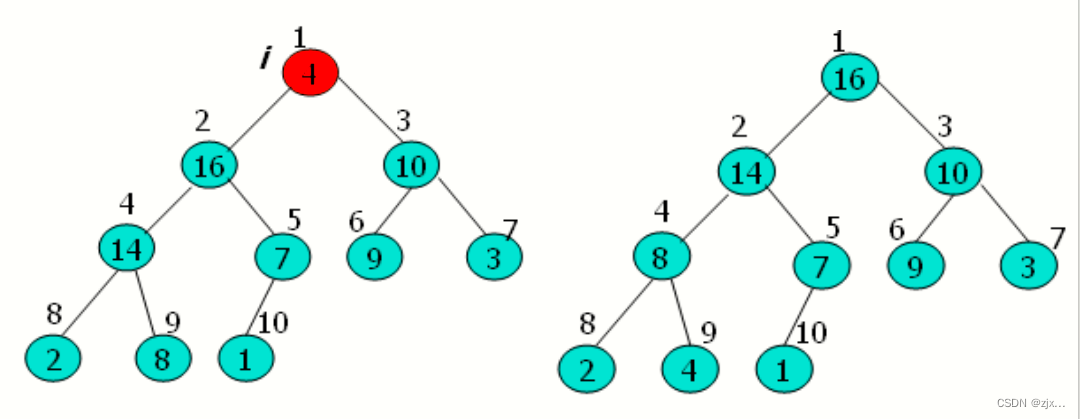


4. 堆排序
4.1 堆排序思路
1. 在完成大根堆建立的基础上,我们将 A[ 1 ] 的值与 A[ A.length ] 互换,然后在堆中去掉节点n(通过减少heap_size实现)。
2. 剩余节点中新的根节点可能会违背大根堆性质,然后我们通过调用MAX-HEAP函数构造一个新的大根堆。
3. 不断重复此过程,直到堆的大小从 n-1 降到 2。
4.2 堆排序过程示意图

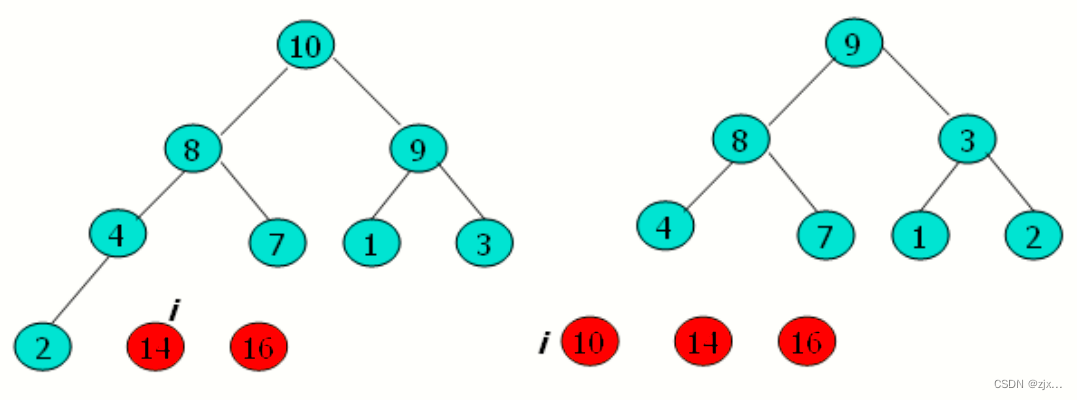

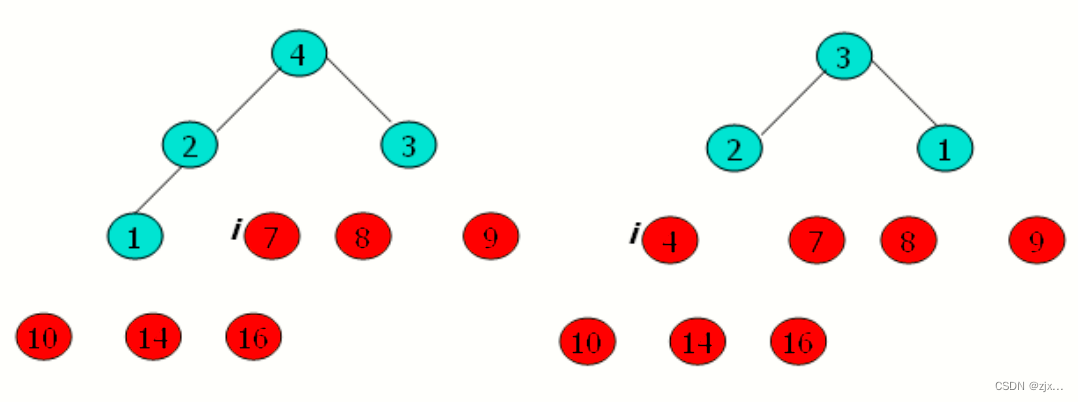

4.3 堆排序伪代码
- HEAPSORT(A)
- BUILD-MAX-HEAP(A)
- for i = A.length downto 2
- exchange A[1] with A[i]
- A.heap-szie = A.heap-size - 1
- MAX-HEAPIFY(A,1)
4.4 C语言完整堆排序代码
- # include
- using namespace std;
- void MAX_HEAPIFY(int A[], int i,int heap_size)
- {
- int l = i * 2;
- int r = i * 2 + 1;
- int largest = 0;
- if (l <= heap_size && A[l] > A[i])
- {
- largest = l;
- }
- else {
- largest = i;
- }
- if (r <= heap_size && A[r] > A[largest])
- {
- largest = r;
- }
- if (largest != i)
- {
- swap(A[i], A[largest]);
- MAX_HEAPIFY(A, largest, heap_size);
- }
- }
- void BUILD_MAX_HEAP(int A[],int A_length)
- {
- int heap_size = A_length;
- for (int i = A_length / 2; i >= 1; i--)
- {
- MAX_HEAPIFY(A, i, heap_size);
- }
- }
- void HEAPSORT(int A[],int A_length)
- {
- BUILD_MAX_HEAP(A, A_length);
- int heap_size = A_length;
- for (int i = A_length; i >= 2; i--)
- {
- swap(A[1], A[i]);
- heap_size = heap_size - 1;
- MAX_HEAPIFY(A, 1,heap_size);
- }
- }
- int main()
- {
- int A[11] = { 0,4,1,3,2,16,9,10,14,8,7 };
- int A_length = 10;
- HEAPSORT(A, A_length);
- cout << "heapsort result:";
- for (int i = 1; i <= 10; i++)
- {
- cout << A[i] << " ";
- }
- return 0;
- }
heapsort result:1 2 3 4 7 8 9 10 14 16
4.5 堆排序时间复杂度
调用 BUILD-MAX-HEAP 函数建堆时间花费 O( n ),每调用一次 MAX-HEAPIFY 函数维护堆花费 O(logn),共调用 n - 1次,故,堆排序的时间复杂度为 O(n*logn)。
5. 优先队列
5.1 优先队列简介
堆这一数据结构的基本操作有:
- 维护堆
- 建堆
- 堆排序
优先队列在堆的基本操作上又添加了:
- INSERT(S,x):向堆S中插入元素x
- MAXIMUM(S):返回堆中的最大值
- EXTRACT-MAX(S):删除并返回堆S中的最大元素
- INCREASE-KEY(S,x,k):将下标为x处的值改为k
数据结构包括:逻辑结构、物理结构、基本操作。
堆和优先队列的基本操作不同,所以堆和优先队列是两种不同的数据结构。
5.2 优先队列基本操作
INCREASE-KEY(A, i, key) :O( logn )
- INCREASE-KEY(A, i, key)
- if key < A[i]
- then error "new key is smaller than current key"
- A[i] ← key
- while i > 1 and A[PARENT(i)] < A[i]
- do exchange A[i] ↔ A[PARENT(i)]
- i ← PARENT(i)
INSERT( A , key ) :O( logn )- INSERT(A, key)
- heap-size[A] ← heap-size[A] + 1
- A[heap-size[A]] ← -∞
- INCREASE-KEY(A, heap-size[A], key)
MAXIMUM( A ) :O( 1 )- HEAP-MAXIMUM(A)
- return A[1]
EXTRACT-MAX( A ) :O( log n )- EXTRACT-MAX(A)
- if heap-size[A] < 1
- then error "heap underflow"
- max ← A[1]
- A[1] ← A[heap-size[A]]
- heap-size[A] ← heap-size[A] - 1
- MAX-HEAPIFY(A, 1)
- return max
INCREASE-KEY(A, i, 15)示意图:
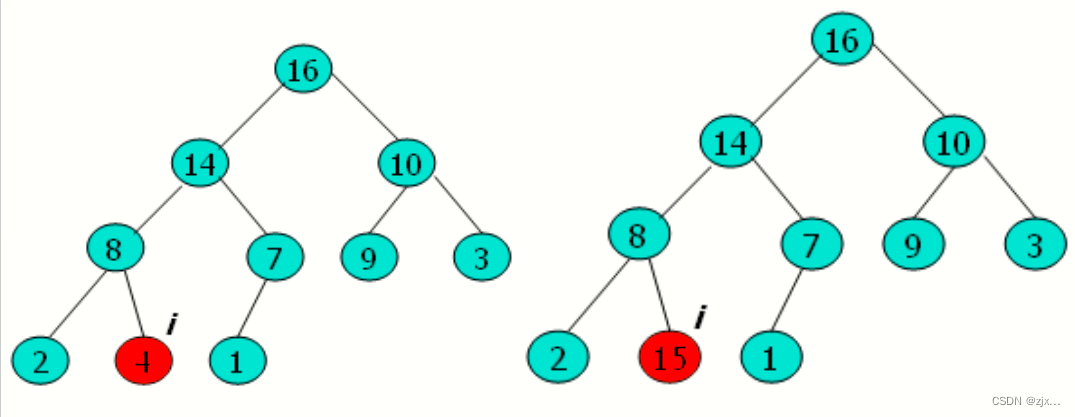
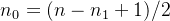
-
相关阅读:
华为OD机考算法题:分班
使用plugin DSL引用自定义gradle plugin
QML android 采集手机传感器数据 并通过udp 发送
图文并茂,让你一探究竟—— 二叉树(附有源码实现)
MyBatis(三、注解开发)
tACS恢复老年人认知控制能力的EEG功能和DTI结构网络机制
高精度室内定位技术,在智慧工厂安全管理的应用
client-go controller-runtime kubebuilder
Linux中mysql的安装、远程访问、基础操作、文件导入
C++17:static_assert实现
- 原文地址:https://blog.csdn.net/qq_64585761/article/details/133042288
