-
2023研究生数学建模D题思路
一、变量的选取
碳排放影响因素的相关性分析,显示第二产业比重与二氧化碳排放之间存在一定的相关关系,同时第二产业比重与地区生产总值之间存在高度的相关;单位GDP 能耗与二氧化碳排放之间存在一定的相关关系,同时单位 GDP 能耗、 能源结构与能源消费总量之间存在相关性, 而单位 GDP能耗、能源结构之间也存在相关关系。因此,为避免在面板数据回归分析的过程中,变量之间多重共线性对回归结果产生影响,同时借鉴已有的影响因素模型,特别是 Kaya 模型、 IPAT 模型,将人口、地区生产总值、能源消费总量作为解释变量,而将第二产业比重、单位 GDP 能耗、能源结构作为控制变量。对人口、地区生产总值、能源消费总量与二氧化碳排放量进行回归分析,分析人口、地区生产总值、能源消费总量、城市化率对二氧化碳排放量的影响。同时,对第二产业比重、单位 GDP 能耗、能源结构、能源价格与人口、地区生产总值、能源消费总量之间进行回归分析,分析第二产业比重、单位 GDP 能耗、能源结构对解释变量的影响。
二、碳排放影响因素模型的回归分析
(1)模型构建


( 2)模型形式选择
一般采用 Hausman 检验法来判断面板数据模型应该选用固定效应还是随机效应模型。 Hausman 检验法的原假设与备择假设设定如下:H0:随机效应回归模型
H1:固定效应回归模型
如果 Hausman 检验的 P 值大于 0.05,则接受假设 H0,选择随机效应回归模型,若 P 值小于 0.05,则拒绝假设 H0,接受假设 H1,选择固定效应回归模型。利用 Eviews6.0 软件进行 Hausman 检验的结果显示, Hausman 检验的 P 值为0.0001,小于 0.05,说明在 5%的显著水平下拒绝原假设为随机效应模型的假设,应该选用固定效应模型进行回归分析。(3)回归分析
依据平稳性检验和 Hausman 检验的分析结果,以及式 4-3 的模型形式,利用Eviews6.0 软件对建立的碳排放影响因素模型进行最小二乘法回归分析。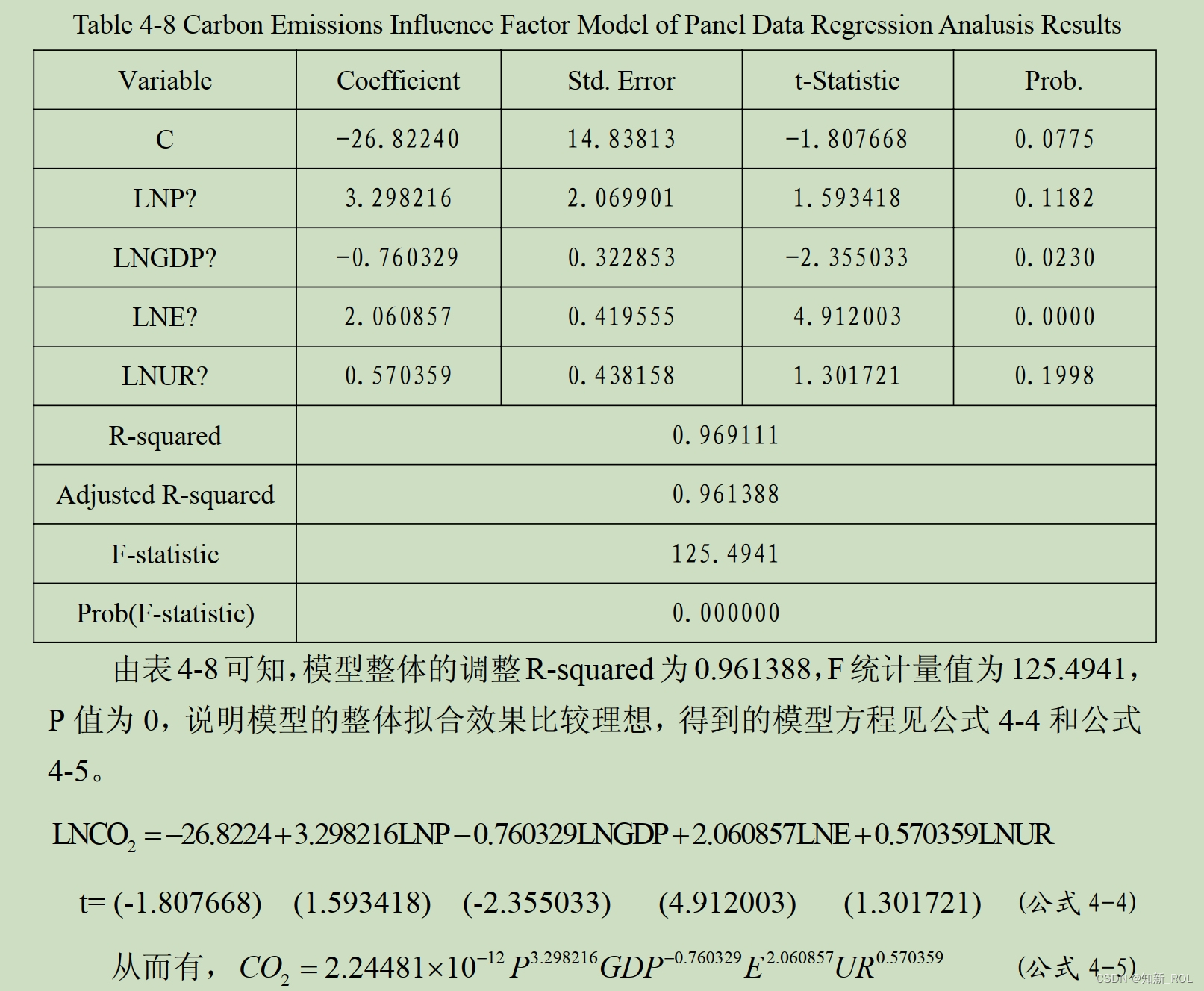
回归结果显示:人口因素 LNP 对 CO2 总量的回归系数为 3.298216,其 t 统计量值为 1.593418, p 值为 0.1182,大于 0.05,说明在 5%的显著水平下,人口因素对 CO2 总量的正向影响并不显著;地区生产总值 LNGDP 对 CO2 总量的影响系数为-0.760329,其 t 统计量值为-2.355033, p 值为 0.0230,小于 0.05,说明在 5%的显著水平下, GDP 对 CO2 总量存在着显著的负向影响; 能源消费总量 LNE 对 CO2总量的影响系数为 2.060857, 其 t 统计量值为 4.912003, p 值为 0.0000, 小于 0.05,说明在 5%的显著水平下,能源消费总量对 CO2 总量存在着显著的正向影响;城市化水平 LNUR 对 CO2 总量的回归系数为 0.570359,其 t 统计量值为 1.301721,p 值为 0.1998,大于 0.05,说明在 5%的显著水平下,城市化率对 CO2 总量的正向影响不显著。 虽然人口和城市化率两个变量在 0.05 显著水平下, 检验结果不显著,但是并未影响整个碳排放影响因素模型的回归结果,模型整体的拟合系数 R 为0.961388, F 统计量值为 125.4941, p 值为 0.0000,说明模型整体的拟合效果比较理想。
三、控制变量的回归分析为进一步分析影响二氧化碳排放的可能性因素,将第二产业比重、单位 GDP能耗、能源结构作为控制变量,利用面板数据回归分析控制变量与碳排放影响因素模型中人口、地区生产总值、能源消费总量之间的数量关系。由于控制变量是通过影响解释变量,间接地影响二氧化碳排放量,所以通过控制变量的面板数据回归,可以找到控制变量与城市二氧化碳排放量之间的关系,从而为干扰方案的设定模拟以及提出城市低碳化发展对策建议提供依据。依据上一节各种碳排放影响因素的相关性分析以及回归方程的结果,对控制变量与解释变量之间、控制变量与控制变量之间可能存在的关系,进行面板数据回归分析。面板数据回归的模型形式选择线性、二次、三次方程模型,通过比较回归方程的拟合优度 R,选择理想的回归方程。三种模型形式如公式 4-6、公式4-7 和公式 4-8 所示。
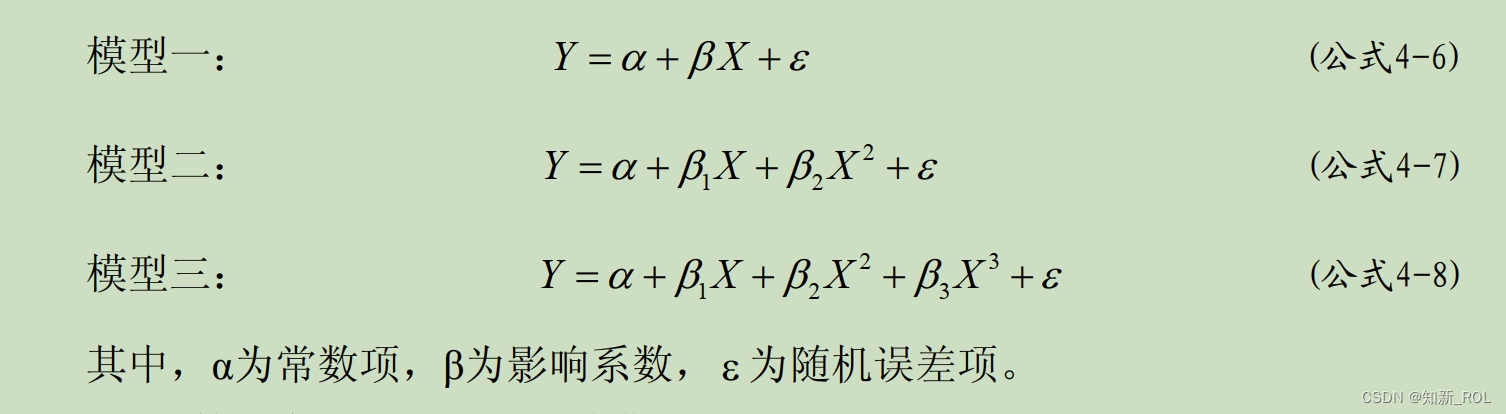
( 1)第二产业比重与能源消费总量
以第二产业比重为解释变量,能源消费总量为被解释变量,以 I 代表第二产业比重,以 E 代表能源消费总量。在分别进行 HUSMAN 检验的基础上,对三个模型进行面板回归分析,结果见表 4-9。
由表 4-9 可知,第二产业比重与能源消费总量三种模型回归的拟合优度 R 都偏低, 虽然二次方程模型的回归结果, 各个变量对被解释变量的影响都是显著的,但是拟合优度 R 只有 0.140739,说明回归结果不理想,这表明第二产业比重对能源消费总量不存在显著的影响。
( 2)第二产业比重与地区生产总值以第二产业比重为解释变量,地区生产总值为被解释变量,以 I 代表第二产
业比重,以 GDP 代表地区生产总值。在分别进行 HUSMAN 检验的基础上,对三
个模型进行面板回归分析,结果见表 4-10。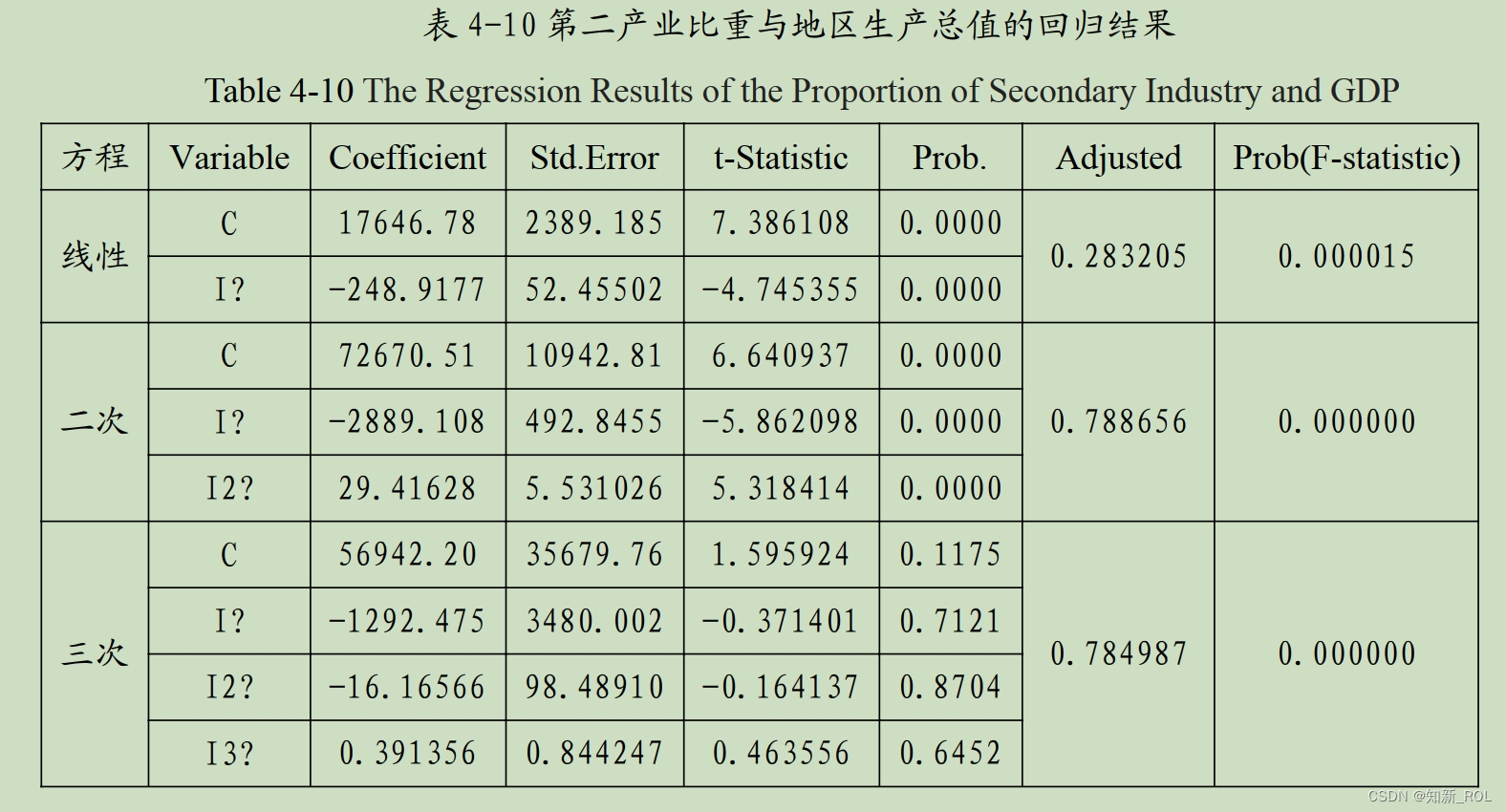
由表4-10可知,二次和三次方程模型回归的调整R方分别为0.788656和0.784987,大于0.7,对应的P值为0,说明两种模型的回归结果都比较理想。但是从变量的回归系数检验可知,在5%显著水平下,二次方程模型的影响系数都是显著的( P<0.05)。因此,应该选用二次方程模型的回归结果,得到的回归方程如公式4-9所示。
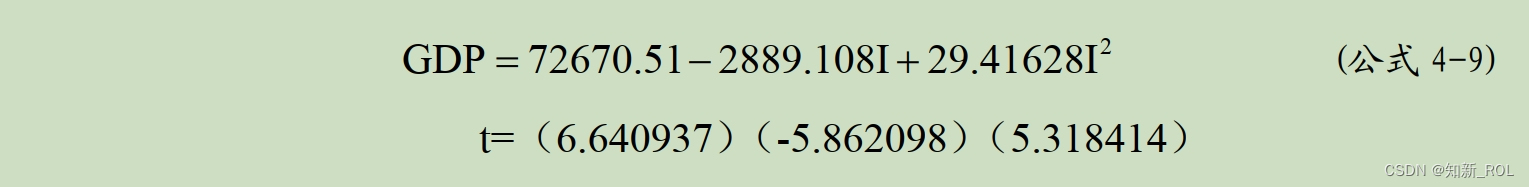
( 3)单位 GDP 能耗与能源消费总量
以单位 GDP 能耗为解释变量,能源消费总量为被解释变量,以 EI 代表单位GDP 能耗(能耗强度),以 E 代表能源消费总量。在分别进行 HUSMAN 检验的基础上,对三个模型进行面板回归分析,结果见表 4-11。
由表4-11可知,三次方程模型回归的调整R方分别为0.976006,最大且对应的P值为0,说明三次方程模型的回归结果比较理想。同时,由变量的回归系数检验可知,在5%显著水平下,三次方程模型的影响系数都是显著的( P<0.05)。因此,应该选用三次方程模型的回归结果,得到的回归方程见公式4-10。

由单位GDP能耗与能源消费总量的回归方程式4-10可知,单位GDP能耗对能源消费总量的影响系数为正,而单位GDP能耗的二次方对能源消费总量的影响为负向,系数为-21552.52,单位GDP能耗三次方对能源消费总量的影响为正向,系数为7609.628,说明整体上单位GDP能耗对能源消费总量存在正向作用。
( 4)能源结构与能源消费总量
以能源结构为解释变量,能源消费总量为被解释变量,以 ES 代表能源结构,以 E 代表能源消费总量。在分别进行 HUSMAN 检验的基础上,对三个模型进行面板回归分析,结果见表 4-12。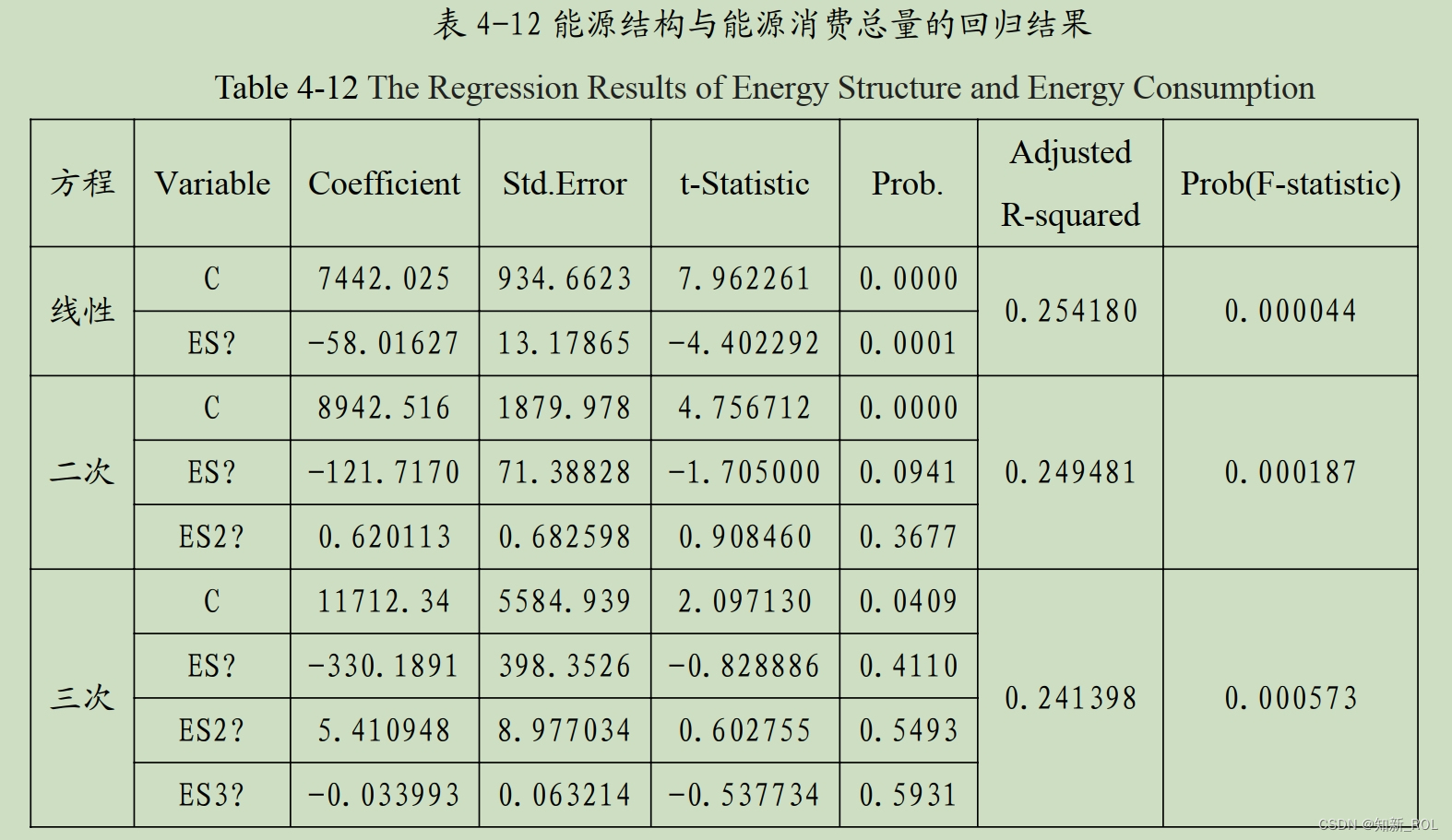
由表 4-12 可知,能源结构与能源消费总量三种模型回归的拟合优度 R 都偏低,三种方程模型回归后调整的 R 方都在 0.25 左右。同时在 5%显著水平下,三种方程变量的回归系数检验, 只有线性方程模型的影响系数都是显著的( P<0.05),而线性方程回归后的拟合优度 R 只有 0.25418,说明回归结果不理想,这表明能源结构对能源消费总量不存在显著的影响。
( 5)能源结构与单位 GDP 能耗
以能源结构为解释变量, 单位 GDP 能耗为被解释变量, 以 ES 代表能源结构,
以 EI 代表单位 GDP 能耗(能耗强度)。在分别进行 HUSMAN 检验的基础上, 对
三个模型进行面板回归分析,结果见表 4-15。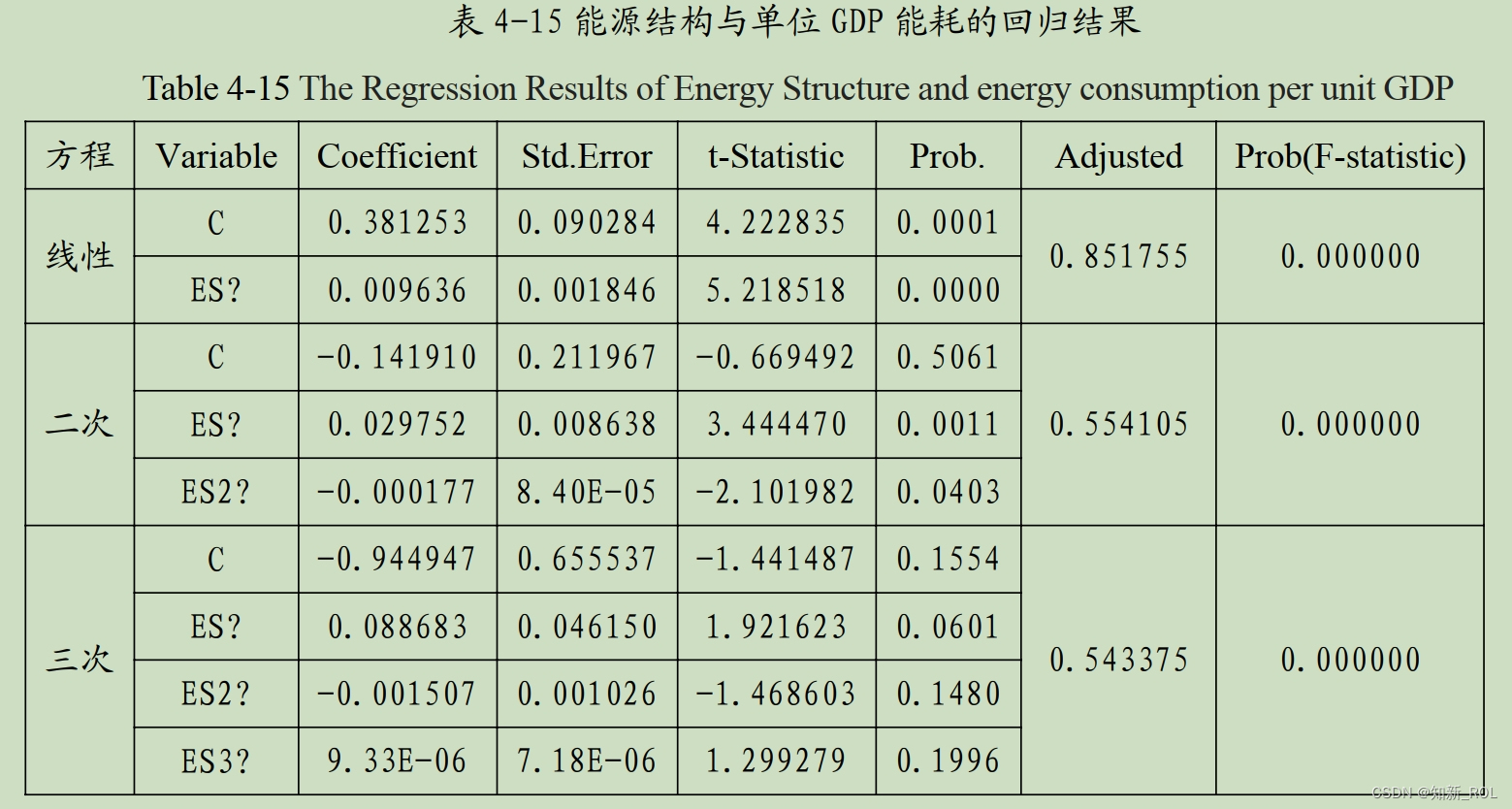
由表4-15可知,线性方程模型回归的调整R方分别为0.851755,最大且对应的P值为0,说明线性方程模型的回归结果比较理想。同时,由变量的回归系数检验可知,在5%显著水平下,线性方程模型的影响系数都是显著的( P<0.05)。因此,应该选择线性方程模型的回归结果,得到的回归方程见公式4-12。

由能源结构与单位GDP能耗的回归方程式4-12可知, 能源结构与单位GDP能耗之间存在着线性关系,且为正向关系,说明当能源结构中煤炭的比例增加时,单位GDP能耗也会增加。
综上所述,人口、地区生产总值、 能源消费总量和城市化率均对城市二氧化碳排放产生直接影响。 同时,依据控制变量的单个面板数据回归,得到第二产业比重与地区生产总值、单位GDP 能耗与能源消费总量、能源价格与能源消费总量的回归方程显示:虽然产业结构与城市二氧化碳排放之间不存在直接地影响,但是产业结构通过对地区生产总值的影响,间接地影响城市碳排放量;单位 GDP 能耗和能源价格与城市二氧化碳排放之间不存在直接影响,但通过对能源消费总量的影响,而间接地影响着城市碳排放量。此外,能源结构、能源价格与单位 GDP 能耗之间也存在着定量关系,面板数据的回归显示:能源结构与单位 GDP 能耗之间存在着正向关系,也就是能源结构中煤炭的比例增加,单位 GDP 能耗也会增加;能源价格与单位GDP 能耗之间存在着负向关系,也就是能源价格上升时,单位 GDP 能耗会下降。
-
相关阅读:
CVE-2022-22963 Spring Cloud Function SpEL命令注入
灯具行业MES解决方案,实现产品的正反向追溯
js知识点getComputedStyle的用法,js获取dom样式的方法
正点原子嵌入式linux驱动开发——Linux INPUT子系统
【rtp-benchmarks】对接发送侧,实现基于uvgRtp的多线程接收
[需求管理-6]:需求分析 - 技术可行性研究与方案设计模板
OpenText 安全取证软件——降低成本和风险的同时,简化电子取证流程
ThreadLocal源码解析 2.ThreadLocalMap内核
五魔方、二阶五魔方
【更新公告】AirtestIDE更新至1.2.17版本
- 原文地址:https://blog.csdn.net/weixin_43608857/article/details/133168436