算法刷题 week4

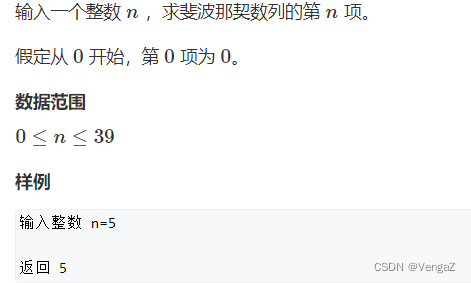
1.斐波那契数列

题目

题解

(递推 + 滚动变量) O(n)

这题的数据范围很小，我们直接模拟即可。
当数据范围很大时，就需要采用其他方式了，可以参考 求解斐波那契数列的若干方法 。

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

用两个变量滚动式得往后计算，a 表示第 n−1 项，b 表示第 n 项。
则令 c=a+b 表示第 n+1 项，然后让 a, b 顺次往后移一位。

时间复杂度分析

总共需要计算 n 次，所以时间复杂度是 O(n) ，但空间复杂度变成了 O(1)。

class Solution {
public:
    const int MOD = 1e9 + 7;    //1000000007
    int Fibonacci(int n) {
        int a = 0, b = 1;
        while (n--)  
        {
            int c = (a + b) % MOD;  //取模优先级比加减高，比乘数低
            a = b, b = c;   //逗号运算符，从左到右计算
        }
        return a;
    }
};  
//  	 0 1 1 2 3 5
//第几项  0 1 2 3 4 5 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

剑指offer 10 - II 青蛙跳台阶问题

题目

题解

此类求 多少种可能性 的题目一般都有 递推性质 ，即 f(n) 和 f(n-1)…f(1) 之间是有联系的。

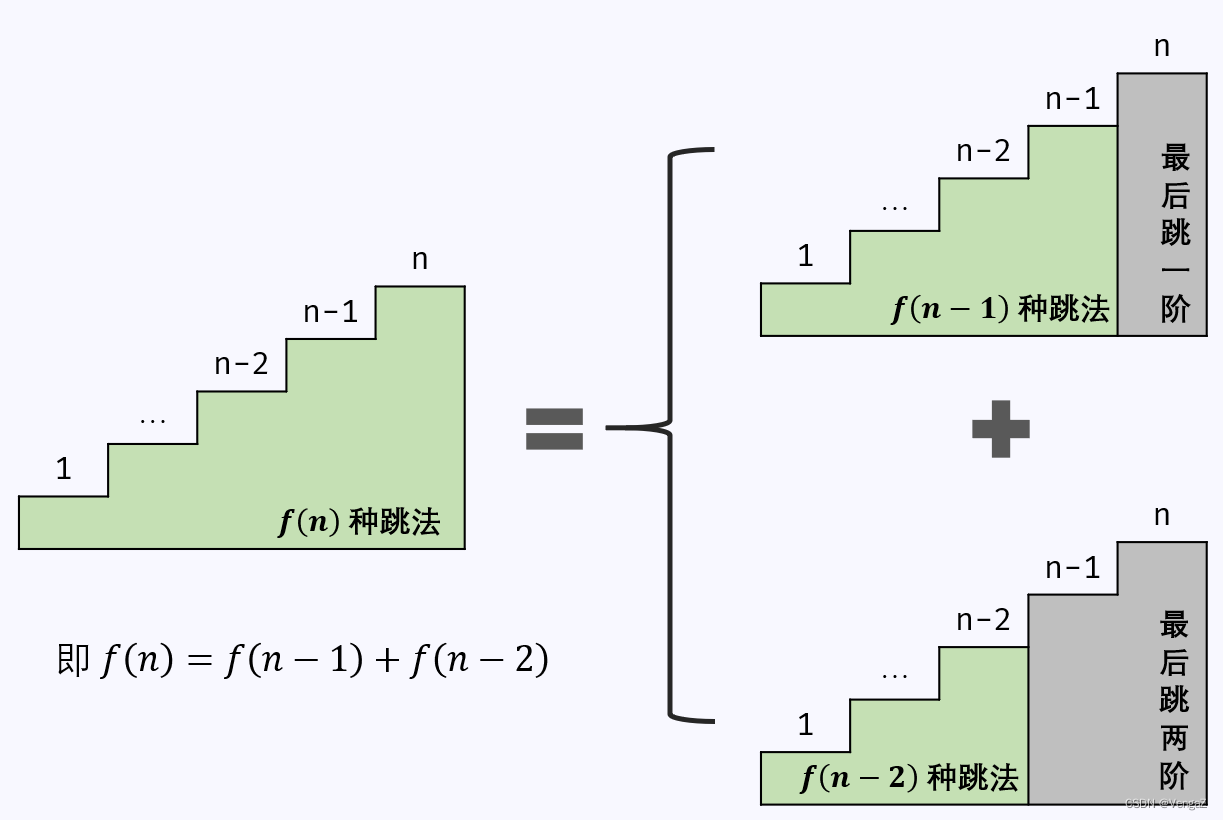
计算 f(n) 需循环 n 次，每轮循环内计算操作使用 O(1) ，所以时间复杂度是 O(n) 。

几个标志变量使用常数大小的额外空间，空间复杂度为 O(1)。

class Solution {
public:
    const int MOD = 1e9 + 7;    //1000000007
    int numWays(int n) {
        int a = 1, b = 1;   //只有起始条件不同，其它都与上题相同
        while (n--)  
        {
            int c = (a + b) % MOD;  //取模优先级比加减高，比乘数低
            a = b, b = c;   //逗号运算符，从左到右计算
        }
        return a;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

10.旋转数组的最小数字

题目

题解

(二分) O(n)

为了便于分析，我们先将数组中的数画在二维坐标系中，横坐标表示数组下标，纵坐标表示数值， 图中水平的实线段表示相同元素。如下所示：

我们发现除了最后水平的一段（黑色水平那段）之外，其余部分满足二分性质：竖直虚线左边的数满足 nums[i]≥nums[0]；而竖直虚线右边的数不满足这个条件。

二分是二分性而不是单调性。只要满足可以找到一个值一半满足一半不满足即可，而不用满足单调性。

分界点就是整个数组的最小值，所以我们先将最后水平的一段删除即可。

另外，不要忘记处理数组完全单调的特殊情况：

当我们删除最后水平的一段之后，如果剩下的最后一个数大于等于第一个数，则说明数组完全单调。

时间复杂度分析

二分的时间复杂度是 O(logn)，删除最后水平一段的时间复杂度最坏是 O(n)，所以总时间复杂度是 O(n)。

class Solution
{
public:
    int findMin(vector<int>& nums)
    {
        int n = nums.size() - 1;
        if(n < 0) return -1;
        
        while (n > 0 && nums[n] == nums[0]) n--; //删除最后水平的一段，当n=0时，只有一个数，也要退出循环
        if (nums[n] >= nums[0]) return nums[0]; //当没有元素旋转时，则出现这种情况
        
        int l = 0, r = n;
        while (l < r) {
            int mid = l + r >> 1;  //[l, mid], [mid + 1, r]
		  	if (nums[mid] < nums[0]) r = mid;
            else l = mid + 1;
        }
        return nums[r];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20