-
大厂面试之算法篇
目录
前言
之前我对算法的理解,仅仅是为了应付大厂的面试。但是在两个月的算法练习中,第一次体会到
编程不仅仅是技术,还是艺术,感受到了编程是一件很酷的事情。比如简单的循环,就可以解决很复杂的数学问题;递归位置的略微变动,就会产生完全不同的结果。
算法对于前端来说重要吗?
这个问题可能在我们所处的不同的阶段里,会有完全不同的理解。我通过系统的练习后,真切的感受到了自己的编程技能在提升,逻辑思维能力有了很大不同。
算法是一个优秀工程师的必备技能,对于提升编码能力有着举重若轻的作用
期待你的答案
文中给出的题目解法,可能不是最优解,希望大家多多指正,一起交流学习,在此表示感谢。一道题的解法,有很多种,对应的时间复杂度与空间复杂度也各不相同,期待你的答案,希望你可以在其中找到
算法的乐趣。算法
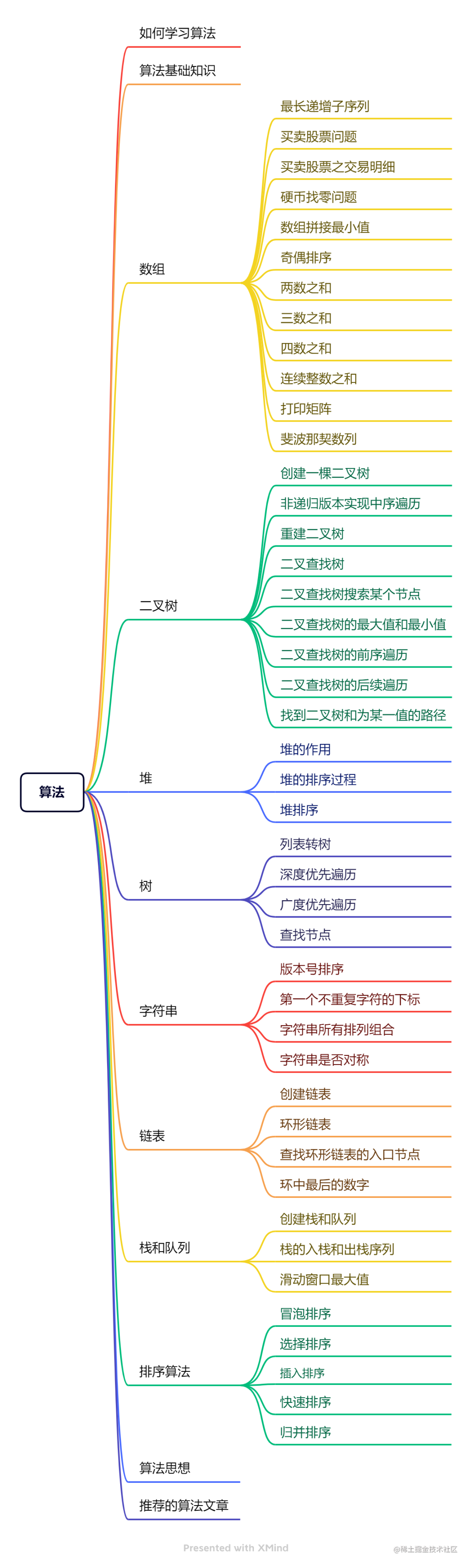
如何学习算法
1、先掌握对应的数据结构
以面试中最常见的二叉树为例。先了解如何创建一个二叉树,通过创建的过程,加深对该数据结构的理解,非常有助于了去解答对应的题目。
2、分类练习
分类练习,即按照每种数据结构进行统一练习。
例如:这段时间只练习二叉树的题目,通过集中的训练,对二叉树有整体的认知。了解前、中、后序遍历的特点、了解二叉搜索树、了解各种题型等体系知识。
同时做好对应的笔记,不建议一上来就直接用leetcode刷题
算法基础知识
时间复杂度
表示代码执行的次数,时间与算法中语句执行次数成正比例,哪个算法中执行语句次数多,它花费的时间就越长,时间复杂度是取代码中最复杂的代码来计算。
时间复杂度按时间的大小,从小到大排序依次是
O(1)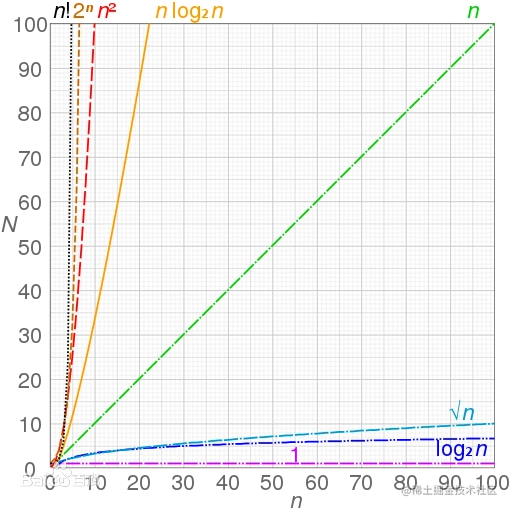
空间复杂度
在算法运算过程中用到的额外的存储空间(不包含原始值的内存大小),反映的对内存占用的趋势,而不是具体内存。
最经典的场景
就是利用空间去换时间,降低时间复杂度,减少计算时间前端 数据结构
数组、栈、队列、树、堆、链表、哈希表、图
数组
数组是最简单、也是最常用的数据结构。数组是可以在内存中连续存储多个元素的结构,在内存中的分配也是连续的。
特点:查询快,增删慢
1)查询快:数组的地址是连续的,我们通过数组的首地址可以找到数组,通过数组的索引可以快速查找某一个元素。
2)增删慢:数组的长度是固定的,我们想要增加/删除一个元素,必须创建一个新的数组,把原数组的数据复制过来。
最长递增子序列
先安排一个非常火的题目,方便小伙伴们热热身。
该算法在vue3 diff算法中有用到,作用是找到最长递归子序列后,可以减少子元素的移动次数。
一个整数数组 nums,找到其中一组最长递增子序列的值。
最长递增子序列是指:子序列中的所有元素单调递增。例如:[3,5,7,1,2,8]的LIS是[3,5,7,8]。- // 该算法用的是动态规划的思想,时间复杂度为n2,并不是最优算法,
- // 最优算法应该是二分查找,最优时间复杂度为nlogn
- function lengthOfLIS(nums) {
- if (!nums.length) return 0;
- // 创建一个和原数组等长的数组dp,用来存储每一项的最长递增子序列,
- // 比如[1,2,2] 表示第二项和第三项的最长递增子序列都为2
- // 该数组每一项初始值都为1,记录当前项的最长递增子序列,
- // 后面的项会在当前项的最长递增子序列个数进行累加
- let dp = new Array(nums.length).fill(1);
- // 双层for循环,每一项都和之前的所有项一一进行比较,
- // 计算出该项的最长递增子序列个数,存储到dp中
- for (let i = 0; i < nums.length; i++) {
- // 当前项依次和之前的每一项进行比较,累加出当前项的最长递增子序列
- for (let j = 0; j < i; j++) {
- if (nums[j] < nums[i]) {
- // 比较当前项已有的最大值和之前项最大值,
- // 比如当比较到第三项[1,2,2]时,如第三项比第二项大,
- // 所以第三项的计算结果为[1,2,3]
- dp[i] = Math.max(dp[i], dp[j] + 1);
- }
- }
- }
- // 取出一组最长递增子序列的具体值
- //(注意:最长递增子序列有可能有多组值,这里是只取出其中一组值)
- // 找到dp中的最大值,该值就是nums的最长递增子序列的个数
- let max = Math.max(...dp);
- let result = [];
- for (let i = max; i >= 1; i--) {
- // 倒序遍历,根据长度获取对应的值
- findArrNode(dp, i, result, nums);
- }
- return result;
- }
- function findArrNode(dp, value, result, arr) {
- // 找到符合条件最后一项的下标,这样才能保证数组的顺序是正确的
- let index = dp.lastIndexOf(value);
- // 存储对应的值
- result.unshift(arr[index]);
- // 对dp进行截取,保证只取最大项之前的数据
- dp.length = index + 1;
- }
- // 测试
- console.log(lengthOfLIS([9, 1, 7, 10, 4, 8, 5, 2]));
- // [1, 4, 5]
- console.log(lengthOfLIS([1, 4, 3, 5, 2, 6, 0]));
- // [1, 3, 5, 6]
亮点:网上一般都是只计算出最长递增子序列的长度,这里计算出一组具体的最长递增子序列的值
力扣上最长上升子序列的视频讲解[1]
买卖股票问题
给定一个整数数组,其中第
i个元素代表了第i天的股票价格;非负整数fee代表了交易股票的手续费用,求返回获得利润的最大值。例如数组为:
[1, 12, 13, 9, 15, 8, 6, 16],fee为2,求获得利润的最大值。注:每笔买卖都需要支付一次手续费。
- /**
- * 贪心算法求解
- * @param {array} list - 股票每天的价格列表
- * @param {number} fee - 手续费
- * */
- function buyStock(list, fee) {
- // min为当前的最小值,即买入点
- let min = list[0],
- sum = 0;
- for (let i = 1; i < list.length; i++) {
- // 从1开始,依次判断
- if (list[i] < min) {
- // 寻找数组的最小值
- min = list[i];
- } else {
- // 计算如果当天卖出是否赚钱
- let temp = list[i] - min - fee;
- if (temp > 0) {
- // 赚钱 存数据
- sum += temp;
- // 关键代码:重新计算min,分两种情况,如果后面继续涨,
- // 则默认继续持有;若后面跌,则以后面的价格重新买入
- min = list[i] - fee;
- }
- }
- }
- return sum;
- }
- console.log(buyStock([1, 12, 13, 9, 15, 8, 6, 16], 2)); // 22
买卖股票之交易明细
继续研究买卖股票问题。通过上题,我们知道
[1, 12, 13, 9, 15, 8, 6, 16]最终的结果为22。但具体的交易明细是什么,哪几天发生了交易,怎么验证22的结果是否正确呢?思路
1) 增加 result 对象,把每笔赚钱的交易都记录下来
2) 新增 minIndex 属性,用来记录每次买入值(最小值)的变化
3) 当 minIndex 不变时,用新的记录替换掉老的记录
4) 遍历 result 对象,取出所存储的交易明细- /**
- * 贪心算法求解交易明细
- * @param {array} list - 股票每天的价格列表
- * @param {number} fee - 手续费
- * */
- function buyStock(list, fee) {
- // 增加result对象,把每笔赚钱的交易都记录下来
- let result = {};
- let min = list[0],
- // 增加minIndex 用来记录每次买入值(最小值)的变化
- minIndex = 0,
- sum = 0;
- for (let i = 1; i < list.length; i++) {
- if (list[i] < min) {
- minIndex = i;
- min = list[i];
- } else {
- let temp = list[i] - min - fee;
- if (temp > 0) {
- sum += temp;
- min = list[i] - fee;
- // 赚钱 存数据
- // 当minIndex不变时,用新的记录替换调老的记录
- result[minIndex] = [list[minIndex], list[i]];
- }
- }
- }
- let arr = [];
- // 遍历result对象,取出所存储的交易明细
- Object.keys(result).forEach(key => {
- arr.push(result[key]);
- });
- return {
- sum,
- arr
- };
- }
- console.log(buyStock([1, 12, 13, 9, 15, 8, 6, 16], 2));
- // 打印结果: {sum: 22, arr: [[1, 13], [9, 15], [6, 16]]}
3次交易明细
1买入,13卖出;
9买入,15卖出;
6买入,16卖出22 = (13 - 1 - 2) + (15 - 9 -2) + (16 - 6 - 2)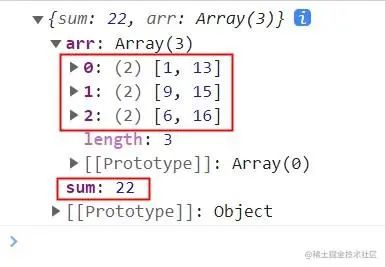
硬币找零问题
给定不同面额的硬币,coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的
最少的硬币个数,如果没有任何一种硬币组合能组成总金额,返回 -1。示例:输入 coins =
[1, 2, 5], amount =11;输出3- function findCoins(coins, amount) {
- if (coins.length === 0) return -1;
- // 用于保存每个目标总额对应的最小硬币个数
- const f = [];
- // 提前定义已知情况
- f[0] = 0;
- // 遍历 [1, amount] 这个区间的硬币总额
- for (let i = 1; i <= amount; i++) {
- // 求的是最小值,因此我们预设为无穷大,确保它一定会被更小的数更新
- f[i] = Infinity;
- // 循环遍历每个可用硬币的面额
- for (let j = 0; j < coins.length; j++) {
- // 若硬币面额小于目标总额,则问题成立
- if (i - coins[j] >= 0) {
- // 状态转移方程
- f[i] = Math.min(f[i], f[i - coins[j]] + 1);
- }
- }
- }
- // 若目标总额对应的解为无穷大,
- // 则意味着没有一个符合条件的硬币总数来更新它,本题无解,返回-1
- if (f[amount] === Infinity) {
- return -1;
- }
- // 若有解,直接返回解的内容
- return f[amount];
- }
- console.log(findCoins([1, 2, 5], 11)); // 3
LeetCode 19.凑零钱问题 动态规划[2]
数组拼接最小值
一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
如
[3, 45, 12],拼接的最小值为12345思路:利用sort排序
a 和 b 两个数字可以有两种组合:ab 和 ba,若 ab < ba 则 ab 排在 ba 前面
- function printMinNumber(arr) {
- if (!arr || arr.length == 0) return null;
- // sort底层是快排
- return arr.sort(compare).join("");
- }
- // 找到ab 和 ba 这两种组合的最小值
- function compare(a, b) {
- let front = `${a}${b}`;
- let after = `${b}${a}`;
- return front - after;
- }
- let arr = [3, 45, 12];
- console.log(printMinNumber(arr)); // 12345
奇偶排序
一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分。
思路: 设定两个指针
1)第一个指针 start,从数组第一个元素出发,向尾部前进
2)第二个指针 end,从数组的最后一个元素出发,向头部前进
3)start 遍历到偶数,end 遍历到奇数时,交换两个数的位置
4)当 start > end 时,完成交换- function exchangeOddEven(arr) {
- let start = 0;
- let end = arr.length - 1;
- // 当start > end时,完成交换
- while (start < end) {
- // 找到第一个偶数
- while (arr[start] % 2 === 1) {
- start++;
- }
- // 找到第一个奇数
- while (arr[end] % 2 === 0) {
- end--;
- }
- // 重点:始终要加上 start < end的限制,否则会出现中间两个数的位置交换错误
- if (start < end) {
- // 奇数和偶数交换位置
- [arr[start], arr[end]] = [arr[end], arr[start]];
- }
- }
- return arr;
- }
- let test = [2, 4, 5, 3, 1];
- console.log(exchangeOddEven(test)); // [1, 3, 5, 4, 2]
两数之和
给定一个整数数组
nums和一个目标值target。在该数组中找出和为目标值的两个整数,并返回他们。要求时间复杂度:O(n)思路:利用map存储已遍历的元素 (典型的空间换时间)
- // 时间复杂度O(n)、 空间复杂度O(n)
- function twoNumAdd(arr, target) {
- if (Array.isArray(arr)) {
- // 使用map将遍历过的数字存起来
- let map = {};
- for (let i = 0; i < arr.length; i++) {
- // 从map中查找是否有key 等于 target-nums[I],
- // 如果取到了,则条件成立,返回结果
- if (map[target - arr[i]] !== undefined) {
- return [target - arr[i], arr[i]];
- } else {
- // 条件不成立,则将已遍历的值存起来
- map[arr[i]] = i;
- }
- }
- }
- return [];
- }
- console.log(twoNumAdd([8, 2, 6, 5, 4, 1, 3], 7));
- // [2, 5]
三数之和
给定一个数组nums,判断 nums 中是否存在三个元素
a,b,c,使得a + b + c = target。找出所有满足条件且不重复的三元组合。思路:
将数组排序,然后固定数组中某一项,用
双端指针的方式,查到两数之和加上该项的值等于目标值,将三数之和转化为两数之和。题目中说明可能会出现多组结果,所以我们要考虑好去重
1)为了方便去重,我们首先将数组从小到大排列
2)对数组进行遍历,取当前遍历的数
nums[i]为一个基准数3)在寻找数组中设定两个起点,最左侧的
left(i+1)和最右侧的right(length-1)4)判断
nums[i] + nums[left] + nums[right]是否等于目标值target5)如果相等,存储该结果,并分别将left和right各移动一位
6)如果大于目标值,将right向左移动一位,向结果逼近
7)如果小于目标值,将left向右移动一位,向结果逼近
8)一轮遍历结束后i++,进入下一轮查询
- function findThree(arr, target) {
- arr.sort();
- let result = [];
- for (let i = 0; i < arr.length; i++) {
- // 跳过重复的arr[i]值, 比如[2, 1, 1],跳过第二个1
- if (i && arr[i] === arr[i - 1]) continue;
- let left = i + 1;
- let right = arr.length - 1;
- while (left < right) {
- let sum = arr[i] + arr[left] + arr[right];
- if (sum > target) {
- right--;
- } else if (sum < target) {
- left++;
- } else {
- // arr[left++], 先取arr[left],然后left++, 两步合成一步;
- // arr[right--]同样的逻辑
- result.push([arr[i], arr[left++], arr[right--]]);
- while (arr[left] === arr[left - 1]) {
- // 跳过重复的arr[left]值,
- left++;
- }
- while (arr[right] === arr[right + 1]) {
- // 跳过重复的arr[right]值
- right--;
- }
- }
- }
- }
- return result;
- }
- console.log(findThree([5, 2, 1, 1, 3, 4, 6], 8));
- // [1, 1, 6] [1, 2, 5] [1, 3, 4]
四数之和
给定一个整数数组nums,判断 nums 中是否存在四个元素
a,b,c,d,使得a + b + c + d = target,找出所有满足条件且不重复的四元组合。思路
到这里其实我们就能发现一些规律,可以像三数之和那样,通过大小指针来逼近结果,从而达到降低一层时间复杂度的效果(重点:将4个数相加,转化为三个数,降低层级)
不管是几数之和,都可以用这种方法来进行降级优化
- function findFour(arr, target) {
- if (arr.length < 4) return [];
- let result = [];
- arr.sort();
- // 最外层控制循环次数,循环次数为arr.length - 3
- for (let i = 0; i < arr.length - 3; i++) {
- // 跳过数组中,重复的起始值
- if (i && arr[i] === arr[i - 1]) continue;
- // 因为数组已进行排序,所有一旦超过目标值,那么以后的值也都比目标值大,
- // 所以可以直接结束这一轮循环
- if (arr[i] + arr[i + 1] + arr[i + 2] + arr[i + 3] > target) break;
- for (let j = i + 1; j < arr.length - 2; j++) {
- // 注意范围,第二个值的最小值是倒数第3位(以下的代码和三个数求和的逻辑一致)
- // 跳过数组中,第二个值重复的
- if (j > i + 1 && arr[j] === arr[j - 1]) continue;
- // 第三个数的下标
- let left = j + 1;
- let right = arr.length - 1;
- while (left < right) {
- let sum = arr[i] + arr[j] + arr[left] + arr[right];
- if (sum > target) {
- right--;
- } else if (sum < target) {
- left++;
- } else {
- // 坑点,注意添加后,left++, right--, 确保循环继续执行
- result.push([arr[i], arr[j], arr[left++], arr[right--]]);
- while (arr[left] === arr[left - 1]) {
- // 跳过重复的值
- left++;
- }
- while (arr[right] === arr[right + 1]) {
- // 跳过重复的值
- right--;
- }
- }
- }
- }
- }
- return result;
- }
- console.log(findFour([2, 1, 5, 4, 3, 6, 0, 7], 10));
- // [0, 1, 2, 7] [0, 1, 3, 6] [0, 1, 4, 5] [0, 2, 3, 5] [1, 2, 3, 4]
连续整数之和
输入一个正整数
S,打印出所有和为S的连续整数序列。例如:输入
15,连续整数序列有:1+2+3+4+5 = 4+5+6 = 7+8 = 15,所以打印出3个连续序列1-5,5-6和7-8。思路:
1)创建一个容器child,用于表示当前的子序列,初始元素为1,2
2)记录子序列的开头元素small和末尾元素big
3)big向右移动子序列末尾增加一个数;small向右移动子序列开头减少一个数
4)当子序列的和大于目标值,small向右移动,子序列的和小于目标值,big向右移动
- function FindContinuousSequence(sum) {
- let result = [];
- // 记录当前的结果
- let child = [1, 2];
- let small = 1; // 初始值1
- let big = 2; //
- let currentSum = 3; // 当前数字之和
- while (big < sum) {
- // big等于sum时,child中只剩一个数,不满足连续正数序列的要求,结束循环
- while (currentSum < sum && big < sum) {
- child.push(++big);
- // currentSum为当前child的和
- currentSum += big;
- }
- while (currentSum > sum && small < big) {
- child.shift();
- // 因为删除了最小值,所以small也要响应变化,增加1
- currentSum -= small++;
- }
- if (currentSum === sum && child.length > 1) {
- // child.length大于1,剔除一个数等于sum的情况
- // child.slice返回一个新的数组
- result.push(child.slice());
- child.push(++big);
- currentSum += big;
- }
- }
- return result;
- }
- console.log(FindContinuousSequence(15));
- // [1, 2, 3, 4, 5] [4, 5, 6] [7, 8]
打印矩阵
输入:
[ [ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ] ]要求输出:
[1,2,3,6,9,8,7,4,5]题目要求的是按照顺时针的顺序,从外向内遍历每一个元素,并将他们按顺序返回出来
- function printMatrix(arr) {
- // map函数用来完成当前矩阵最外一圈的遍历
- // @param1{Array}二维数组 arr 表示当前矩阵
- // @param2{Array}一维数组 result 用来保存遍历结果
- let map = (arr, result) => {
- // 矩阵的高度即行数
- let n = arr.length;
- // 遍历矩阵的每一行
- for (let i = 0; i < n; i++) {
- // 若第一行 按顺序插入
- if (i === 0) {
- result = result.concat(arr[i]);
- } else if (i === n - 1) {
- // 若最后一行 倒序插入
- result = result.concat(arr[i].reverse());
- } else {
- // 若中间行 插入该行最后一个元素 并将该元素从矩阵中删除
- result.push(arr[i].pop());
- }
- }
- // 将已经遍历的第一行和最后一行从矩阵中删除
- arr.pop();
- arr.shift();
- // 遍历插入最左侧一列 此时删除首位两行后矩阵高度已变为n-2
- for (let j = n - 3; j >= 0; j--) {
- // 避免arr[j]长度为空时插入undefined
- if (arr[j].length) {
- result.push(arr[j].shift());
- }
- }
- // 截止条件 矩阵有元素就继续递归
- if (arr.length) {
- // 把已将遍历元素删除的矩阵进行递归
- return map(arr, result);
- } else {
- return result;
- }
- };
- // 将初始矩阵传入, 保存结果的数组初始为空
- return map(arr, []);
- }
- let matrix = [
- [1, 2, 3],
- [4, 5, 6],
- [7, 8, 9]
- ];
- console.log(printMatrix(matrix));
- // [1, 2, 3, 6, 9, 8, 7, 4, 5]
斐波那契数列
从第3项开始,当前项等于前两项之和:
1 1 2 3 5 8 13 21⋯⋯使用动态规划,将复杂的问题拆分,也就是:
F(N) = F(N - 1) + F(N - 2),然后用数组将已经计算过的值存起来。- function fib(n) {
- // 使用dp数组,将之前计算的结果存起来,防止栈溢出
- let dp = [];
- dp[0] = 1n; // bigint 可以用来表示超过2^53-1的大整数
- dp[1] = 1n;
- for (let i = 2; i <= n; i++) {
- dp[i] = dp[i - 1] + dp[i - 2]; // 注意:arr[i]
- }
- return dp[n];
- }
- console.log(fib(1000));
二叉树
二叉树是树结构中一种典型的结构,每个节点最多只能有两个子节点,一个是左侧子节点,一个是右侧子节点。
二叉树图例
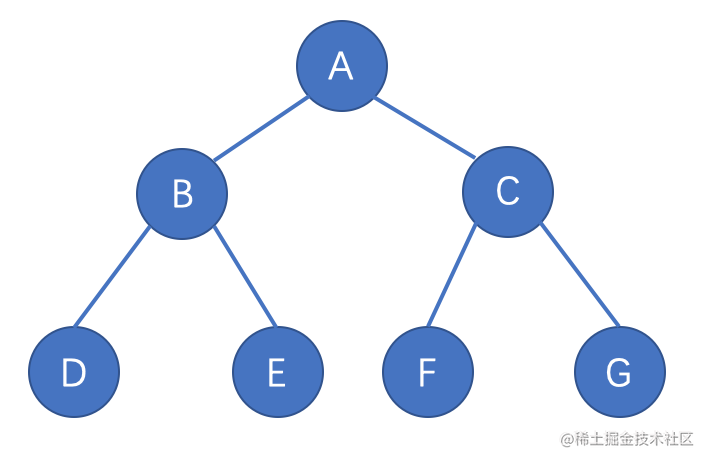
二叉树遍历的规律
前序遍历:根节点 + 左子树前序遍历 + 右子树前序遍历
中序遍历:左子树中序遍历 + 根节点 + 右子数中序遍历
后序遍历:左子树后序遍历 + 右子树后序遍历 + 根节点创建一棵二叉树
要求:若新节点的值比父节点小,则放到父节点的左子树上;反之放到右子树上。
- // 二叉树节点
- class Node {
- constructor(data, left = null, right = null) {
- this.data = data;
- this.left = left;
- this.right = right;
- }
- }
- // 构建二叉树
- class Tree {
- constructor() {
- this.root = null;
- }
- insert(data) {
- var node = new Node(data, null, null);
- // 创建根节点
- if (!this.root) {
- this.root = node;
- return;
- }
- var current = this.root;
- var parent = null;
- while (current) {
- parent = current;
- // 值比父节点小,放到父节点的左子树上
- if (data < parent.data) {
- current = current.left;
- // 找到最左侧的节点,将新的节点设置为该节点的左子树节点
- if (!current) {
- parent.left = node;
- return;
- }
- } else {
- // 值比父节点大,放到父节点的右子树上
- current = current.right;
- if (!current) {
- parent.right = node;
- return;
- }
- }
- }
- }
- // 定义前序遍历的方法
- static preOrder(node, arr = []) {
- if (node) {
- arr.push(node.data);
- this.preOrder(node.left, arr);
- this.preOrder(node.right, arr);
- }
- return arr;
- }
- // 定义中序遍历的方法
- static middleOrder(node, arr = []) {
- if (node) {
- this.middleOrder(node.left, arr);
- arr.push(node.data);
- this.middleOrder(node.right, arr);
- }
- return arr;
- }
- // 定义后序遍历的方法
- static laterOrder(node, arr = []) {
- if (node) {
- this.laterOrder(node.left, arr);
- this.laterOrder(node.right, arr);
- arr.push(node.data);
- }
- return arr;
- }
- // 获取二叉树的最大层级
- static getDeep(node, deep = 0) {
- if (!node) {
- return deep;
- }
- deep++;
- // 获取左子树的层级
- let left = this.getDeep(node.left, deep);
- // 获取右子树的层级
- let right = this.getDeep(node.right, deep);
- // 取层级最大的值
- return Math.max(left, right);
- }
- }
- // 创建二叉树,依次插入新节点
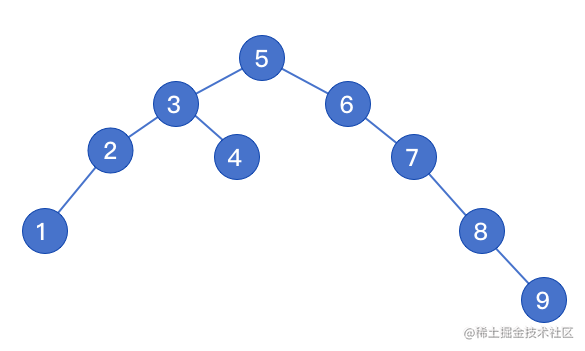
- var t = new Tree();
- t.insert(5);
- t.insert(3);
- t.insert(6);
- t.insert(2);
- t.insert(4);
- t.insert(7);
- t.insert(8);
- t.insert(1);
- t.insert(9);
- // 打印二叉树
- console.log(t);
- // 前序遍历 [5, 3, 2, 1, 4, 6, 7, 8, 9]
- console.log(Tree.preOrder(t.root));
- // 中序遍历 [1, 2, 3, 4, 5, 6, 7, 8, 9]
- console.log(Tree.middleOrder(t.root));
- // 后序遍历 [1, 2, 4, 3, 9, 8, 7, 6, 5]
- console.log(Tree.laterOrder(t.root));
- // 获取二叉树的最大层级:5
- console.log(Tree.getDeep(t.root));
构建结果
非递归版本实现中序遍历
中序遍历的两种方式
1)方式一:递归版本,如上文的
middleOrder方法2)方式二:非递归版本(回溯算法)实现中序遍历
非递归版本的好处:避免循环递归时栈溢出的情况,效率更高
非递归版本流程
1)步骤1 :左孩子入栈 -> 直至左孩子为空的节点
2)步骤2 :节点出栈 -> 访问该节点
3)步骤3 :以右子树为目标节点,再依次执行 步骤1、2、3- function middleTraverse(root) {
- const result = [];
- // stack 用来存储回溯算法中的节点
- const stack = [];
- let current = root;
- while (current || stack.length > 0) {
- // 找到最左侧的节点
- while (current) {
- // 依次将左子树节点存到栈中
- stack.push(current);
- current = current.left;
- }
- // 节点出栈
- current = stack.pop();
- // 存储该节点的值
- result.push(current.data);
- // 获取该节点的右子树节点
- current = current.right;
- }
- return result;
- }
- // t 为上文创建的二叉树
- console.log(middleTraverse(t.root));
- // 打印结果: [1, 2, 3, 4, 5, 6, 7, 8, 9]
重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,重建出该二叉树
原理
前序遍历:根节点 + 左子树前序遍历 + 右子树前序遍历
中序遍历:左子树中序遍历 + 根节点 + 右字数中序遍历重建二叉树流程
1)前序遍历第一个值为根结点
root,然后找到根节点在中序遍历的下标2)将中序遍历 拆分为左子树中序遍历 和 右子树中序遍历
3)将前序遍历 拆分为左子树前序遍历 和 右子树前序遍历
4)利用左子树中序遍历 + 左子树前序遍历,递归创建左子树节点
5)利用右子树中序遍历 + 右子树前序遍历,递归创建右子树节点
6)递归重建二叉树
- // 重建二叉树
- function reConstruction(pre, mid) {
- if (pre.length === 0) {
- return null;
- }
- // 前序遍历长度为1时,该节点为叶子节点
- if (pre.length === 1) {
- return new Node(pre[0]);
- }
- // 前序遍历的第一个值为根节点
- const value = pre[0];
- // 找到根节点在中序遍历的位置
- const index = mid.indexOf(value);
- // 将中序遍历 分为左子树中序遍历 和 右子数中序遍历
- const midLeft = mid.slice(0, index);
- const midRight = mid.slice(index + 1);
- // 左子树前序遍历的长度为index
- // 将前序遍历 分为左子树前序遍历 和 右子树前序遍历
- const preLeft = pre.slice(1, index + 1);
- const preRight = pre.slice(index + 1);
- // 创建根节点
- const node = new Node(value);
- // 利用左子树中序遍历 + 左子树前序遍历,递归创建左子树节点
- node.left = reConstruction(preLeft, midLeft);
- // 递归创建右子树节点
- node.right = reConstruction(preRight, midRight);
- return node;
- }
- class Node {
- constructor(data, left = null, right = null) {
- this.data = data;
- this.left = left;
- this.right = right;
- }
- }
- reConstruction([1, 2, 4, 7, 3, 5, 6, 8], [4, 7, 2, 1, 5, 3, 8, 6]);
重建结果
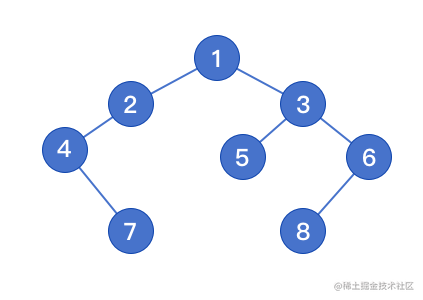
二叉树在线构建工具[3]
二叉查找树
二叉查找树(BST)是二叉树的一种,特点是所有的左节点比父节点的值小,所有的右节点比父节点的值大,并且任意左、右子树也分别为二叉查找树
二叉查找树图例
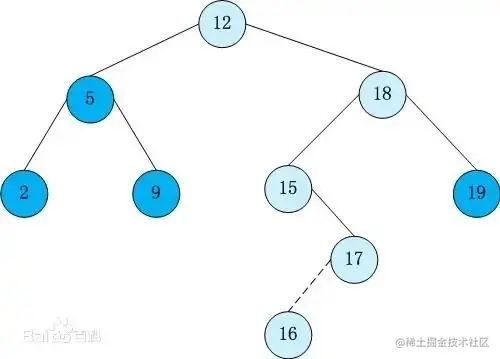
主要作用是搜索和动态排序
二叉查找树搜索某个节点
- // 查找一个节点
- function findNode(data, node) {
- if (node) {
- if (data === node.data) {
- return node;
- } else if (data < node.data) {
- return this.findNode(data, node.left);
- } else {
- return this.findNode(data, node.right);
- }
- } else {
- return null;
- }
- }
- // 查找值为6的节点
- // t 为上文创建的二叉树
- console.log(findNode(6, t.root));
二叉查找树的最大值和最小值
最右侧的节点为二叉查找树的最大值
最左侧的节点为二叉查找树的最小值- // 最大值:最右侧的节点
- function getMax(root) {
- let max = null;
- let current = root;
- while (current !== null) {
- max = current.data;
- current = current.right;
- }
- return max;
- }
- // 最小值:最左侧的节点
- function getMix(root) {
- let mix = null;
- let current = root;
- while (current !== null) {
- mix = current.data;
- current = current.left;
- }
- return mix;
- }
- console.log(getMax(t.root), "max"); // 9
- console.log(getMix(t.root), "min"); // 1
二叉查找树的前序遍历
给一个整数数组,判断该数组是不是某二叉查找树的前序遍历的结果。如果是输出true,否则输出false。
- // 判断一个整数数组,是否为某二叉查找树的前序遍历的结果
- function preOrderOfBST(list) {
- if (list && list.length > 0) {
- // 前序遍历,第一个值为根节点
- var root = list[0];
- // 找到数组中,第一个比根节点大的节点,即为右子树的节点
- for (var i = 0; i < list.length; i++) {
- if (list[i] > root) {
- break;
- }
- }
- // 遍历右子树的节点,要求所有右子树的节点都比根节点大
- for (let j = i; j < list.length; j++) {
- if (list[j] < root) {
- return false;
- }
- }
- var left = true;
- // 同理,递归判断左子树是否符合二叉搜索树的规则
- if (i > 1) {
- left = preOrderOfBST(list.slice(1, i + 1));
- }
- var right = true;
- // 递归判断右子树是否符合二叉搜索树的规则
- if (i < list.length) {
- right = preOrderOfBST(list.slice(i, list.length));
- }
- // 左、右子树 都符合要求,则是一个二叉搜索树
- return left && right;
- }
- }
- console.log(preOrderOfBST([5, 3, 2, 1, 4, 6, 7, 8, 9]));
- // true
二叉查找树的后续遍历
给一个整数数组,判断该数组是不是某二叉搜索树的后续遍历的结果。如果是则输出 true,否则输出 false。
- // 判断一个整数数组,是否为某二叉搜索树的后序遍历的结果
- function laterOrderOfBST(list) {
- if (list && list.length > 0) {
- // 后续遍历,最后一个节点为根节点
- var root = list[list.length - 1];
- for (var i = 0; i < list.length - 1; i++) {
- if (list[i] > root) {
- break;
- }
- }
- for (let j = i; j < list.length - 1; j++) {
- if (list[j] < root) {
- return false;
- }
- }
- var left = true;
- // 判断左子树
- if (i > 0) {
- left = laterOrderOfBST(list.slice(0, i));
- }
- var right = true;
- // 判断右子树
- if (i < list.length - 1) {
- right = laterOrderOfBST(list.slice(i, list.length - 1));
- }
- return left && right;
- }
- }
- console.log(laterOrderOfBST([1, 2, 4, 3, 9, 8, 7, 6, 5]));
- // true
找到二叉树和为某一值的路径
利用回溯算法:如果不符合要求,退回来,换一条路再试找到和为
11的所有路径:结果为[5, 3, 2, 1], [5, 6]二叉树结构如下

- /**
- * 找到和为某一值的路径
- * @param {object} node - 二叉树
- * @param {number} num - 和(目标值)
- * @param {array} stack - 栈
- * @param {number} sum - 当前路径的和
- * @param {array} result - 存储所有的结果
- * */
- function findPath(node, num, stack = [], sum = 0, result = []) {
- stack.push(node.data);
- sum += node.data;
- // 找到所有的节点路径(包含叶子节点和子节点的所有情况之和)
- if (sum === num) {
- // if (!node.left && !node.right && sum === num) {
- // 找到所有的叶子节点路径
- result.push(stack.slice());
- }
- if (node.left) {
- findPath(node.left, num, stack, sum, result);
- }
- if (node.right) {
- findPath(node.right, num, stack, sum, result);
- }
- // 回溯算法:不符合要求,退回来,换一条路再试
- // 叶子节点直接pop;子节点中的所有的节点递归完成后再pop
- stack.pop();
- return result;
- }
- // t 为上文创建的二叉树
- console.log(findPath(t.root, 11));
- // [5, 3, 2, 1], [5, 6]
堆
堆实际上是一棵完全二叉树
大顶堆:每个的节点元素值不小于其子节点
小顶堆: 每个的节点元素值不大于其子节点
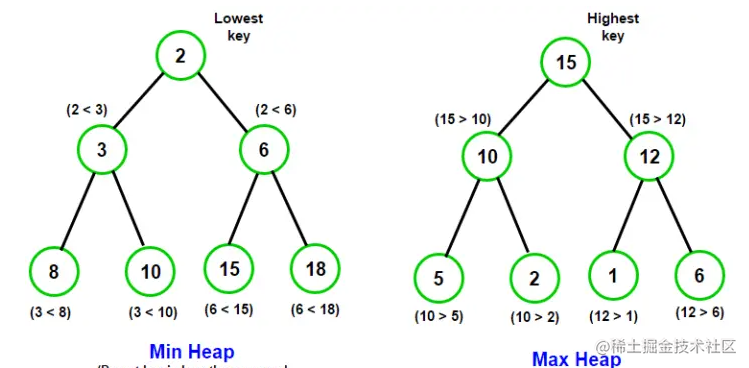
堆的作用
在庞大的数据中,找到最大的m个数或者最小的m个数,可以借助堆来完成这个过程,时间复杂度为
nlogm。如果先排序,再取前m个数,最小时间复杂度
nlogn。nlogm<nlogn,堆排序时间复杂度更优。堆节点与其叶子节点的规律
1)堆中父节点为
k,它的左子节点下标为2k+1,右子节点是2k+22)所有序号大于
length/2的结点都是叶子节点,0到length/2-1为父节点堆的排序过程

堆排序
从一堆数中,找到前m个最小值。如图,从下面的大顶堆中,找到前4个最小值,结果为
[6, 5, 2, 1]。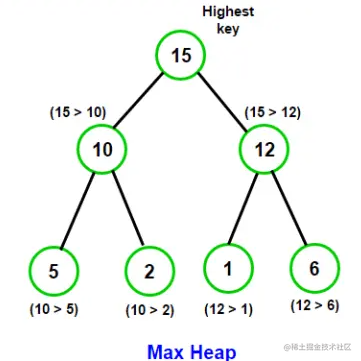
- function heapSort(list, m) {
- if (m > list.length) {
- return [];
- }
- createHeap(list, m);
- for (let i = m; i < list.length; i++) {
- if (list[i] < list[0]) {
- // 找到前m个数的最小值,依次将最小值放到最前面
- [list[i], list[0]] = [list[0], list[i]];
- ajustHeap(list, 0, m);
- }
- }
- // 取出前m个数
- return list.splice(0, m);
- }
- // 构建大顶堆(构建的顺序是从下往上,先找到最后一个父节点,
- // 然后从最后一个父节点开始构建,然后依次往上构建,将最大值逐步替换成根节点)
- function createHeap(arr, length) {
- // 找到堆中所有的非叶子节点(找到最后一个叶子节点,该节点之前都是非叶子节点)
- for (let i = Math.floor(length / 2) - 1; i >= 0; i--) {
- // 堆中,父节点为i,则子节点为2*i+1、2*i+2;
- // 反过来,知道了子节点为length,则最后一个子节点为Math.floor(length / 2) - 1。
- ajustHeap(arr, i, length); // 调整大顶堆,将最大值逐步替换成根节点
- }
- }
- // 调整大顶堆(注意:调整的顺序是从上往下,将根节点替换后,
- // 先调整根节点,然后依次往下调整,对应的子节点如果发生替换,
- // 要重新调整下对应子节点,保证都满足子节点不大于父节点的条件,直到该大顶推全部调整完成)
- // 比如,当调节根节点时,[a0, a1, a2], a2> a0, a2替换a0,
- // 则要重新调节a2这个分支上的节点,保证都满足子节点不大于父节点的条件
- function ajustHeap(arr, index, length) {
- for (let i = 2 * index + 1; i < length; i = 2 * i + 1) {
- // 父节点为i,则子节点为2*i+1
- if (i + 1 < length && arr[i + 1] > arr[i]) {
- // 找到arr[i + 1] 和 arr[i] 中的最大值
- i++;
- }
- // 如果子节点比父节点大,交换两者的位置,将最大值移动到顶部
- if (arr[index] < arr[i]) {
- [arr[index], arr[i]] = [arr[i], arr[index]];
- index = i;
- } else {
- break;
- }
- }
- }
- console.log(heapSort([5, 10, 2, 15, 1, 12, 6], 4));
- // [6, 5, 2, 1]
树
JS中树结构一般类似这样
- let tree = [
- {
- id: "1",
- title: "节点1",
- children: [
- {
- id: "1-1",
- title: "节点1-1"
- },
- {
- id: "1-2",
- title: "节点1-2"
- }
- ]
- },
- {
- id: "2",
- title: "节点2",
- children: [
- {
- id: "2-1",
- title: "节点2-1"
- }
- ]
- }
- ];
列表转树
使用对象存储数据, 典型的空间换时间
时间复杂度为
O(n)、空间复杂度为O(n)- function listToTree(data) {
- // 使用对象重新存储数据, 空间换时间
- let map = {};
- // 存储最后结果
- let treeData = [];
- // 遍历原始数据data,存到map中,id为key,值为数据
- for (let i = 0; i < data.length; i++) {
- map[data[i].id] = data[i];
- }
- // 遍历对象
- for (let i in map) {
- // 根据 parentId 找到的是父节点
- if (map[i].parentId) {
- if (!map[map[i].parentId].children) {
- map[map[i].parentId].children = [];
- }
- // 将子节点 放到 父节点的 children中
- map[map[i].parentId].children.push(map[i]);
- } else {
- // parentId 找不到对应值,说明是根结点,直接插到根数组中
- treeData.push(map[i]);
- }
- }
- return treeData;
- }
- // 测试
- let list = [
- { id: 1, title: "child1", parentId: 0 },
- { id: 2, title: "child2", parentId: 0 },
- { id: 6, title: "child2_1", parentId: 2 },
- { id: 4, title: "child1_1", parentId: 1 },
- { id: 5, title: "child1_2", parentId: 1 },
- { id: 3, title: "child3", parentId: 0 },
- { id: 7, title: "child3_1", parentId: 3 }
- ];
- console.log(listToTree(list));
深度优先遍历
递归实现,写法简单,时间复杂度为
O(n2)- function deepTree(tree, arr = []) {
- tree.forEach(data => {
- arr.push(data.id);
- // 遍历子树
- data.children && deepTree(data.children, arr);
- });
- return arr;
- }
- let tree = [
- {
- id: "1",
- title: "节点1",
- children: [
- {
- id: "1-1",
- title: "节点1-1"
- },
- {
- id: "1-2",
- title: "节点1-2"
- }
- ]
- },
- {
- id: "2",
- title: "节点2",
- children: [
- {
- id: "2-1",
- title: "节点2-1"
- }
- ]
- }
- ];
- console.log(deepTree(tree));
- // ['1', '1-1', '1-2', '2', '2-1']
广度优先遍历
思路
1)维护一个队列,队列的初始值为树结构根节点组成的列表,重复执行以下步骤,直到队列为空
2)取出队列中的第一个元素,进行访问相关操作,然后将其后代元素(如果有)全部追加到队列最后
时间复杂度为
O(n)、空间复杂度为O(n)- // 广度优先
- function rangeTree(tree, arr = []) {
- let node,
- list = [...tree];
- while ((node = list.shift())) {
- arr.push(node);
- node.children && list.push(...node.children);
- }
- return arr;
- }
- let tree = [
- {
- id: "1",
- title: "节点1",
- children: [
- {
- id: "1-1",
- title: "节点1-1"
- },
- {
- id: "1-2",
- title: "节点1-2"
- }
- ]
- },
- {
- id: "2",
- title: "节点2",
- children: [
- {
- id: "2-1",
- title: "节点2-1"
- }
- ]
- }
- ];
- console.log(rangeTree(tree));
- // ['1', '2', '1-1', '1-2', '2-1']
查找节点
递归实现,写法简单
- function findTreeNode(tree, func) {
- for (const data of tree) {
- // 条件成立 直接返回
- if (func(data)) return data;
- if (data.children) {
- const res = findTreeNode(data.children, func);
- // 结果存在再返回
- if (res) return res;
- }
- }
- return null;
- }
- let tree = [
- {
- id: "1",
- title: "节点1",
- children: [
- {
- id: "1-1",
- title: "节点1-1"
- },
- {
- id: "1-2",
- title: "节点1-2"
- }
- ]
- },
- {
- id: "2",
- title: "节点2",
- children: [
- {
- id: "2-1",
- title: "节点2-1"
- }
- ]
- }
- ];
- console.log(
- findTreeNode(tree, data => {
- return data.title === "节点1-1";
- })
- );
- // 打印结果: {id: '1-1', title: '节点1-1'}
字符串
版本号排序
比较
a, b两个版本大小:a为1.rc.2.1,b为1.beta.2。其中rc > beta > alpha。例子 1.2.3 < 1.2.4 < 1.3.0.alpha.1 < 1.3.0.alpha.2 < 1.3.0.beta.1 < 1.3.0.rc.1 < 1.3.0。要求:当 a > b 是返回 1;当 a = b 是返回 0;当 a < b 是返回 -1;
思路
1)首先先写一个映射表,建立不同版本的映射关系
2)将不同版本的英文字母,替换成对应的数字,转化为对字符串进行比较
3)字符串比较的原则:取出相同位置的数字进行递归比较
- function compareVersion(str1, str2) {
- // 创建rc beta alpha,对应的权重值,将版本号转化为纯数字
- let map = { rc: 3, beta: 2, alpha: 1 };
- Object.keys(map).forEach(key => {
- str1 = str1.replace(key, map[key]);
- str2 = str2.replace(key, map[key]);
- });
- const arr1 = str1.split(".");
- const arr2 = str2.split(".");
- function fn(arr1, arr2) {
- let i = 0;
- while (true) {
- // 取出相同位置的数字
- const s1 = arr1[i];
- const s2 = arr2[i];
- i++;
- // 若s1 或 s2 不存在,说明相同的位置已比较完成,
- // 剩余的位置比较arr1 与 arr2的长度,长的版本号大
- if (s1 === undefined || s2 === undefined) {
- return arr1.length - arr2.length;
- }
- if (s1 === s2) continue;
- // 比较相同位置的数字大小
- return s1 - s2;
- }
- }
- return fn(arr1, arr2);
- }
- // 测试
- let str1 = "1.rc.2.1";
- let str2 = "1.beta.2";
- console.log(compareVersion(str1, str2));
- // 1
第一个不重复字符的下标
输入一个字符串,找到第一个不重复字符的下标
如输入
abcabcde, 输出6, 第一个不重复的字符为d- // 方法一:
- // 先使用Set去重
- // 然后两层遍历,时间复杂度为O(n2)
- function findAlone(str) {
- let arr = str.split("");
- // 通过set 去重
- let aloneArr = [...new Set(arr)];
- let val = "";
- for (let i = 0; i <= aloneArr.length - 1; i++) {
- // 用原始字符串进行遍历 找到唯一的值
- if (arr.filter(item => item == aloneArr[i]).length == 1) {
- val = aloneArr[i];
- break;
- }
- }
- return val ? arr.indexOf(val) : -1;
- }
- let str = "abcabcde";
- console.log(findAlone(str)); // 6
- // 方法二:
- // 思路: 使用map存储每个字符出现的次数
- // 该方法时间复杂度和空间复杂度均为O(n), 从时间上来说,要比第一种方法快
- function findAlone1(str) {
- if (!str) return -1;
- // 使用map存储每个字符出现的次数
- let map = {};
- let arr = str.split("");
- arr.forEach(item => {
- let val = map[item];
- // val为undefined时,表示未存储,map[item] = 1;
- // 否则map[item] = val + 1
- map[item] = val ? val + 1 : 1;
- });
- // 一次遍历结果后,再遍历一遍找到出现1次的值
- for (let i = 0; i < arr.length; i++) {
- if (map[arr[i]] == 1) {
- return i;
- }
- }
- return -1;
- }
- console.log(findAlone1(str));
- // 6
字符串所有排列组合
输入一个字符串,打印出该字符串中字符的所有排列组合。
例如输入字符串
abc,则打印出由字符a,b,c所能排列出来的所有字符串,结果为:['abc', 'acb', 'bca', 'bac', 'cab', 'cba']。思路:
1)利用回溯法(将删除的元素递归后,重新添加到数据中)
2)每次递归,固定开头的字母,比如abc,先固定a,然后交换bc的位置,拿到两个结果 abc acb
3)然后交换字符串位置,比如abc递归一轮后,位置变化为 bca
4)第二轮,固定b,然后交换ca的位置,拿到两个结果 bca bac
5)同理,依次将字符串中的字符放到头部,并固定,拿到所有情况的结果
- /**
- * 计算所有字符串的组合
- * @param {array} list - 字符串列表
- * @param {array} result - 最终的结果
- * @param {string} current - 当前的字符串
- * @param {string} temp - 当前固定的字符
- * */
- function stringGroup(list = [], result = [], current = "", temp = "") {
- current += temp;
- if (list.length === 0) {
- // 递归的出口,将对应结果添加到list中
- return result.push(current);
- }
- for (let i = 0; i < list.length; i++) {
- // 每次递归 固定第一个字符
- temp = list.shift();
- stringGroup(list, result, current, temp);
- // 将删除的temp 重新添加到queue尾部,实现将数组反转的效果,
- // 如[a,b,c]反转为[c,b,a]
- list.push(temp);
- }
- // 这里去重是解决str中有重复的字母,比如str为'aacd'
- return [...new Set(result)];
- }
- console.log(stringGroup("abc".split("")));
- // ['abc', 'acb', 'bca', 'bac', 'cab', 'cba']
字符串是否对称
输入一个字符串,判断是否对称,对称输出ture,不对称输出false。
输入
abcba; 输出true。- // 方法一: 将字符串切分为数组,再逆序,再连接为字符串
- function isReserveSame(str) {
- let temp = str
- .split("")
- .reverse()
- .join("");
- return temp === str;
- }
- console.log(isReserveSame("abcba"));
- // true
- // 方法二: 循环遍历,判断对称位置的字符是否相等
- function isReserveSame1(s) {
- let flag = true;
- for (let i = 0; i < parseInt(s.length / 2); i++) {
- if (s.charAt(i) !== s.charAt(s.length - 1 - i)) {
- flag = false;
- }
- }
- return flag;
- }
- console.log(isReserveSame1("abcba"));
- // true
链表
链表:用一组任意存储的单元来存储线性表的数据元素。一个对象存储着本身的值和
next(下一个元素)的地址。链表是物理存储单元上非连续的、非顺序的存储结构。链表特点:查询慢,增删快
1)查询慢:链表地址不是连续的,每次查询都要从头开始
2)增删快:增加/删除一个元素,对链表的整体结构没有影响,所以增删快
链表在开发中也是会用到的数据结构,比如
React的?Fiber和hook底层都用到了链表链表图例
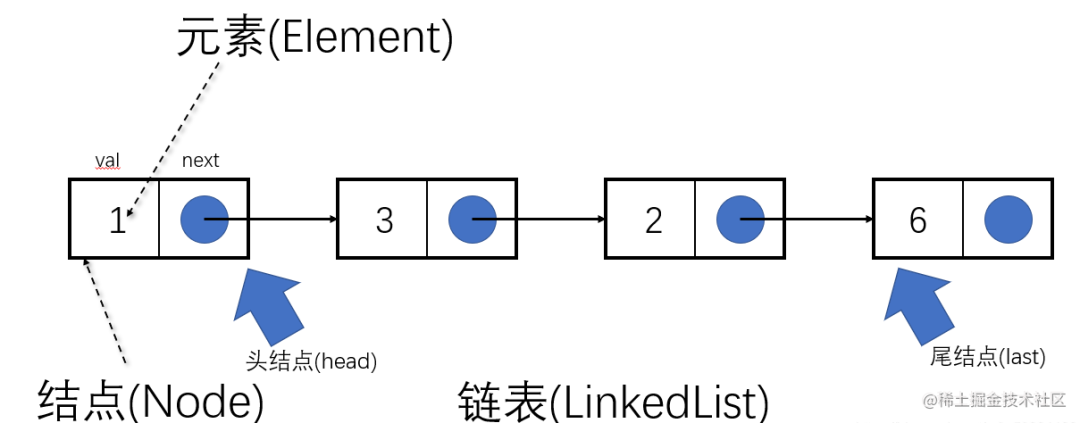
创建链表
- // 链表Node节点
- function Node(data) {
- this.data = data;
- this.next = null;
- }
- // 创建链表
- class LinkedList {
- constructor() {
- this.count = 0; // 链表长度
- this.head = null; // 链表开头
- }
- // 添加节点
- push(data) {
- let node = new Node(data);
- if (!this.head) {
- this.head = node;
- } else {
- let current = this.head;
- while (current.next) {
- current = current.next;
- }
- current.next = node;
- }
- this.count++;
- }
- // 插入节点
- insert(data, index) {
- if (index >= 0 && index <= this.count) {
- let node = new Node(data);
- let current = this.head;
- if (index == 0) {
- // 插到表头
- this.head = node;
- node.next = current;
- } else {
- for (let i = 0; i < index - 1; i++) {
- // 找到要插入位置的前一个元素
- current = current.next;
- }
- let next = current.next; // 暂存next以后的节点信息
- current.next = node;
- node.next = next;
- }
- this.count++;
- // 返回插入成功的结果
- return true;
- } else {
- return false;
- }
- }
- // 按索引值查找
- getIndexNode(index) {
- if (index >= 0 && index < this.count) {
- let current = this.head;
- for (let i = 0; i < index; i++) {
- current = current.next;
- }
- return current;
- } else {
- return null;
- }
- }
- // 按索引值删除节点
- removeNode(index) {
- if (index >= 0 && index < this.count) {
- if (index == 0) {
- this.head = this.head.next;
- } else {
- let current = this.head;
- const pre = this.getIndexNode(index - 1);
- // 找到要删除元素的前一个元素
- current = pre.next; // 获取要删除的元素
- pre.next = current.next;
- }
- this.count--;
- return true;
- } else {
- return false;
- }
- }
- // 查找节点的位置
- indexOf(data) {
- let current = this.head;
- for (let i = 0; i < this.count; i++) {
- if (data === current.data) {
- return i;
- }
- current = current.next;
- }
- }
- // 链表转字符串
- toString() {
- let current = this.head;
- let string = `${current.data}`;
- // current长度大于1,取下一个节点
- if (this.count > 1) current = current.next;
- for (let i = 1; i < this.count; i++) {
- string = `${string},${current.data}`;
- current = current.next;
- }
- return string;
- }
- }
- // 测试
- const link = new LinkedList();
- // 增加5个节点
- for (let i = 1; i <= 5; i++) {
- link.push(i);
- }
- // 索引为1的位置 插入节点6
- link.insert(6, 1);
- // 获取索引2的节点
- console.log(link.getIndexNode(2));
- // 删除索引3的节点
- console.log(link.removeNode(3));
- // 查找位为6的索引
- console.log(link.indexOf(6));
- // 链表转字符串 1,6,2,4,5
- console.log(link.toString());
环形链表
链表其中一个节点的next指针,指向另一个节点
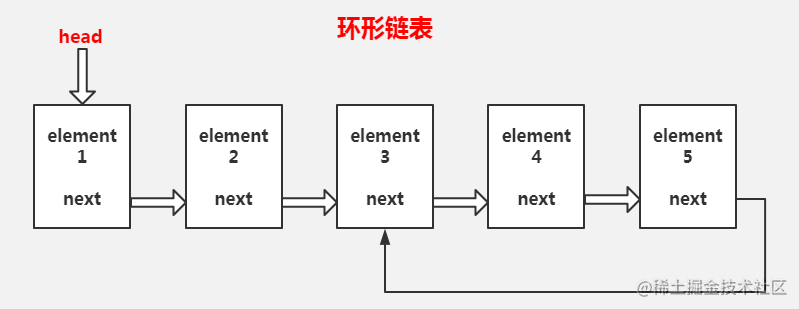
创建如上图所示的链表,节点5指向节点3
- const link = new LinkedList();
- // 增加5个节点
- for (let i = 1; i <= 5; i++) {
- link.push(i);
- }
- // 创建环形链表,找到值为5的节点,将该节点的next指向值为3的节点
- link.getIndexNode(4).next = link.getIndexNode(2);
查找环形链表的入口节点
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null
思路
声明两个指针
P1 P21)判断链表是否有环:P1 P2 从头部出发,P1一次走两步,P2一次走一步,如果可以相遇,则环存在
2)从环内某个节点开始计数,再回到此节点时得到链表环的长度 length
3)P1、P2 回到head节点,让 P1 先走 length 步 ,当P2和P1相遇时即为链表环的节点
- // 查找环形链表节点
- function EntryNodeOfLoop(head) {
- if (!head || !head.next) {
- return null;
- }
- let p1 = head.next;
- // p2一次走两步
- let p2 = head.next.next;
- // 若p1 === p2 则证明该链表有环
- while (p1 !== p2) {
- if (p1 == null || p2.next === null) {
- return null;
- }
- p1 = p1.next;
- p2 = p2.next.next;
- }
- // 此时p1 是 p1、p2重合的点
- let temp = p1;
- let length = 1;
- p1 = p1.next;
- // 获取环的长度
- while (p1 !== temp) {
- p1 = p1.next;
- length++;
- }
- // 找公共节点
- // 此时为什么要将p1 p2重新赋值,因为p2只是重合的点,不一定是入口节点
- p1 = p2 = head;
- while (length-- > 0) {
- p2 = p2.next;
- }
- while (p1 !== p2) {
- p1 = p1.next;
- p2 = p2.next;
- }
- return p1;
- }
- const link = new LinkedList();
- // 增加5个节点
- for (let i = 1; i <= 5; i++) {
- link.push(i);
- }
- // 创建环形链表,值为5的节点,next指向值为3的节点
- link.getIndexNode(4).next = link.getIndexNode(2);
- console.log(EntryNodeOfLoop(link.head)); // 打印节点3
环中最后的数字
0,1,...,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字,求出这个圆圈里剩下的最后一个数字约瑟夫环问题

- // 使用链表形成一个闭环,最后一个元素的指针指向第一个元素
- function findLastNode(n, m) {
- if (n < 1 || m < 1) return -1;
- const head = { val: 0 };
- let current = head;
- for (let i = 1; i < n; i++) {
- // 生成一个链表
- current.next = { val: i };
- // 将next下一项赋值给current
- current = current.next;
- }
- // 尾部指向头部,形成闭环
- current.next = head;
- while (current.next != current) {
- // 此时current是最后一个节点
- for (let i = 0; i < m - 1; i++) {
- // 找到要删除节点的前一个节点(范围是m-1,
- // 这里是从最后一个节点开始;如果是从head开始,范围则是m-2)
- current = current.next;
- }
- // 删除第m个节点
- current.next = current.next.next;
- }
- return current.val;
- }
- console.log(findLastNode(5, 3)); // 3
栈和队列
栈是一种特殊的线性表,仅能在线性表的一端操作,栈顶允许操作,栈底不允许操作。
栈的特点是:先进后出,从栈顶放入元素的操作叫入栈,取出元素叫出栈。
队列与栈一样,也是一种线性表,不同的是,队列可以在一端添加元素,在另一端取出元素,也就是:先进先出,从一端放入元素的操作称为入队,取出元素为出队。
两者区别:
栈(先进后出)、队列(先进先出)创建栈和队列
创建栈
- // 创建栈 只能从栈尾添加和删除 实现先进后出的效果
- class Stack {
- constructor() {
- this.arr = [];
- }
- // 从栈尾添加
- insert(data) {
- this.arr.push(data);
- }
- // 从栈尾删除
- del() {
- return this.arr.pop();
- }
- toString() {
- return this.arr.toString();
- }
- }
- let stack = new Stack();
- stack.insert(1);
- stack.insert(2);
- stack.insert(3);
- stack.del();
- console.log(stack.toString()); // 1,2
创建队列
- // 创建队列 只能从栈尾添加和头部删除 实现先进先出的效果
- class Queue {
- constructor() {
- this.arr = [];
- }
- insert(data) {
- this.arr.push(data);
- }
- del() {
- return this.arr.shift();
- }
- toString() {
- return this.arr.toString();
- }
- }
- let queue = new Queue();
- queue.insert(1);
- queue.insert(2);
- queue.insert(3);
- queue.del();
- console.log(queue.toString()); // 2,3
栈的入栈和出栈序列
输入两个整数序列,第一个序列
arr1表示栈的入栈顺序,请判断第二个序列arr2,是否可能为该栈的出栈序列思路
1)创建一个栈,模拟入栈、出栈的过程
2)
id用来记录arr1已出栈的位置3)当
stack栈顶元素和arr2栈顶元素相同时,stack出栈;索引id+14)最终stack栈为空,表示arr1全部元素已出栈
- // 判断两个整数序列,第一个序列为入栈顺序,第二个序列是否为出栈顺序
- function isSameStack(arr, arr1) {
- // 创建一个栈,模拟入栈、出栈的过程
- let stack = [];
- // id用来记录arr1已出栈的位置
- let id = 0;
- for (let i = 0; i < arr.length; i++) {
- // 入栈
- stack.push(arr[i]);
- // 当stack栈顶元素和 arr1 栈顶元素相同时,stack出栈;索引id+1,
- while (stack.length && stack[stack.length - 1] === arr1[id]) {
- // 出栈
- stack.pop();
- // 下次要对比arr1[id+1]与stack栈顶元素是否相等
- id++;
- }
- }
- // 最终stack栈为空,表示arr全部元素已出栈
- return stack.length == 0;
- }
- console.log(isSameStack([1, 2, 3, 4, 5], [2, 4, 5, 3, 1])); // true
滑动窗口最大值
给定一个数组
nums,有一个大小为k的滑动窗口,从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口中的k个数字。滑动窗口每次只向右移动一位,求返回滑动窗口最大值。如
nums = [1,3,-1,-3,5,3,6,7],k = 3,输出结果为[3, 3, 5, 5, 6, 7]。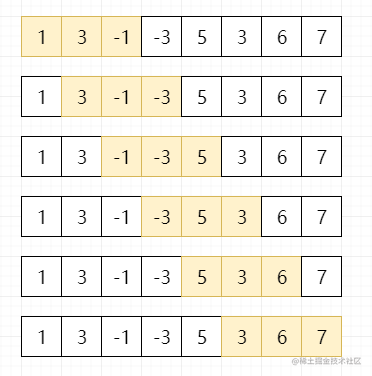
思路
利用双端队列(队列两侧都可以剔除元素),窗口移动的过程中,始终保证window中最左侧的元素为当前窗口的最大值。
- function maxSlidingWindow(nums, k) {
- // window存储当前窗口中数据的下标
- const window = [];
- // result存储窗口中的最大值
- const result = [];
- for (let i = 0; i < nums.length; i++) {
- if (i - window[0] > k - 1) {
- // 窗口不断往右移动,当最大值在窗口最左侧,但窗口的长度超出k时的情况,
- // 就要把左侧的最大值剔除,比如窗口为【3,-1,-3】,继续往右时,就要把左侧的3剔除
- window.shift(); // 剔除窗口长度超出范围时左侧的最大值
- }
- for (let j = window.length - 1; j >= 0; j--) {
- // 当前窗口的值依次和要插入的值做比较,如果小于要插入的值,剔除掉该值,
- // 直到window为空为止(保证window中最左侧的值为最大值)
- if (nums[window[j]] <= nums[i]) {
- window.pop();
- }
- }
- // 添加右侧新加入的值,插入新值时有两种情况:
- // 1、新值为最大值时,则window此时为空;
- // 2、新值不为最大值时,window已剔除掉比新值小的值。
- // 始终保证window中最左侧的值为最大值
- window.push(i);
- if (i >= k - 1) {
- // 窗口是从0开始移动,当移动的距离,大于等于目标范围后,
- // 以后再往后移动一次,就要写入当前窗口的最大值
- result.push(nums[window[0]]);
- }
- }
- return result;
- }
- console.log(maxSlidingWindow([1, 3, -1, -3, 5, 3, 6, 7], 3));
- // [3, 3, 5, 5, 6, 7]
排序算法
各种排序算法的对比详情
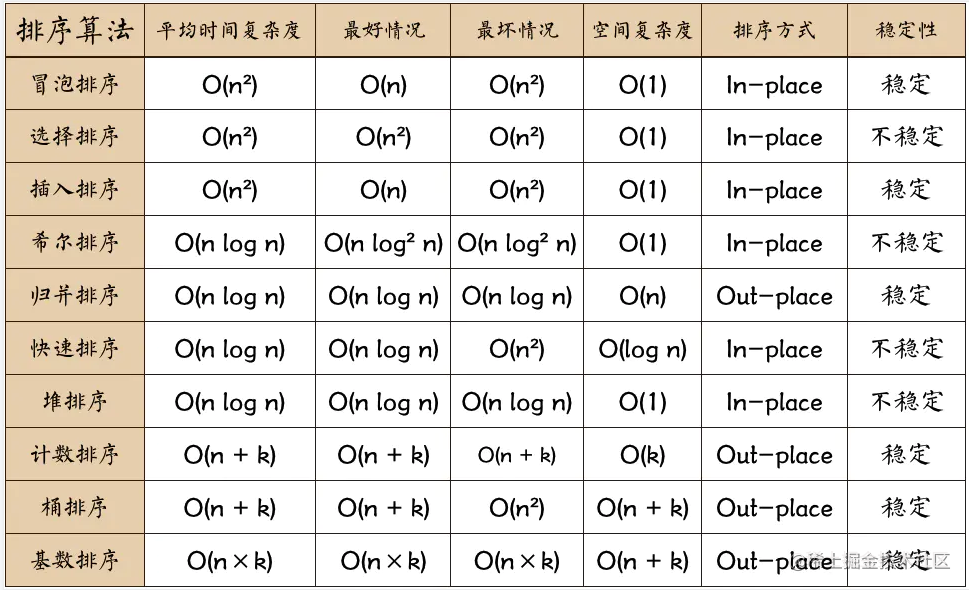
算法的稳定性:序列相同元素排序后,先后次序不变即稳定
冒泡排序、归并排序稳定,快速排序、选择排序不稳定
冒泡排序
时间复杂度为
O(n2),稳定- function bubbleSort(arr) {
- const length = arr.length;
- // 外层循环用控制 排序进行多少轮
- for (let i = 0; i < length; i++) {
- // 内层循环用于每一轮的数据比较
- // 注意j的长度范围 length - i - 1
- for (let j = 0; j < length - i - 1; j++) {
- // 相邻元素,大的放到后面
- if (arr[j] > arr[j + 1]) {
- // 交换位置
- [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
- }
- }
- }
- return arr;
- }
- console.log(bubbleSort([8, 7, 1, 4, 3])); // [1,3,4,7,8]
选择排序
时间复杂度为
O(n2),不稳定思路
从未排序序列中找到最小的元素,放到已排序序列的头部,重复上述步骤,直到所有元素排序完毕。
1)外层循环控制进行多少轮
2)内层循环进行数据比较,找到每一轮的最小值
- function selectSort(arr) {
- // 定义index存储最小值的下标
- let index;
- // 外层循环用控制 排序进行多少轮
- for (let i = 0; i < arr.length - 1; i++) {
- index = i;
- // 内层循环用于每一轮的数据比较
- // 注意j的起始范围是 i + 1
- for (let j = i + 1; j < arr.length; j++) {
- // 寻找最小值
- if (arr[j] < arr[index]) {
- // 保存最小值的下标
- index = j;
- }
- }
- // 如果 index 不是目前的头部元素,则交换两者
- if (index !== i) {
- [arr[i], arr[index]] = [arr[index], arr[i]];
- }
- }
- return arr;
- }
- console.log(selectSort([9, 1, 5, 3, 2, 8]));
- // [1, 2, 3, 5, 8, 9]
插入排序
时间复杂度为
O(n2),稳定思路
将左侧序列看成一个有序序列,每次将一个数字插入该有序序列。
插入时,从有序序列最右侧开始比较,若比较的数较大,后移一位。

- function insertSort(array) {
- // 外层控制循环的次数
- for (let i = 1; i < array.length; i++) {
- let target = i;
- // 内层循环用于每一轮的数据比较
- for (let j = i - 1; j >= 0; j--) {
- if (array[target] < array[j]) {
- [array[target], array[j]] = [array[j], array[target]];
- target = j;
- } else {
- break;
- }
- }
- }
- return array;
- }
- console.log(insertSort([9, 1, 5, 3, 2, 8]));
- // [1, 2, 3, 5, 8, 9]
快速排序
时间复杂度为
O(nlogn),不稳定思路
1)以一个数为基准(中间的数),比基准小的放到左边,比基准大的放到右边
2)再按此方法对这两部分数据分别进行快速排序(递归进行)
3)不能再分后退出递归,并重新将数组合并
- // 快速排序
- function quickSort(list) {
- // 当list.length <= 1时,退出递归
- if (list.length <= 1) return list;
- // 找到中间节点
- let mid = Math.floor(list.length / 2);
- // 以中间节点为基准点,比该节点大的值放到right数组中,否则放到left数组中
- let base = list.splice(mid, 1)[0];
- let left = [];
- let right = [];
- list.forEach(item => {
- if (item > base) {
- right.push(item);
- } else {
- left.push(item);
- }
- });
- // 重新组合数组
- return quickSort(left).concat(base, quickSort(right));
- }
- console.log(quickSort([9, 1, 5, 3, 2, 8]));
归并排序
时间复杂度为
O(nlogn),稳定思路
1)将给定的列表分为两半(如果列表中的元素数为奇数,则使其大致相等)
2)以相同的方式继续划分子数组,直到只剩下单个元素数组
3)从单个元素数组开始,合并子数组,以便对每个合并的子数组进行排序
4)重复第 3 步单元,直到最后得到一个排好序的数组。

- function MergeSort(array) {
- let len = array.length;
- if (len <= 1) {
- return array;
- }
- // 将给定的列表分为两半
- let num = Math.floor(len / 2);
- let left = MergeSort(array.slice(0, num));
- let right = MergeSort(array.slice(num, array.length));
- return merge(left, right);
- function merge(left, right) {
- let [l, r] = [0, 0];
- let result = [];
- while (l < left.length && r < right.length) {
- if (left[l] < right[r]) {
- result.push(left[l]);
- l++;
- } else {
- result.push(right[r]);
- r++;
- }
- }
- result = result.concat(left.slice(l, left.length));
- result = result.concat(right.slice(r, right.length));
- return result;
- }
- }
- console.log(MergeSort([6, 5, 3, 1, 8, 7, 2, 4]));
算法思想
常见的6种算法思想
递归
优点:使用范围广,简单容易上手
缺点:递归太深,容易发生栈溢出(比如斐波那契数列使用递归进行计算)
使用场景:比如树的遍历、快排、深拷贝、查找字符串的所有组合等
分治算法
思想:将某问题分成若干个子问题,然后解决多个子问题,将子问题的解合并得到最终结果,
比如快速排序(以中间元素为基准,将原来的数组拆分为左右两个数组,依次类推)
使用场景:快速排序、二分查找、归并排序
贪心算法
最终得到的结果并不一定是整体最优解,可能只是比较好的结果
但是贪心算法在很多问题上还是能够拿到最优解或较优解,所以它的存在还是有意义的
使用场景:买卖股票
回溯算法
回溯算法是一种搜索法,试探法,它会在每一步做出选择,一旦发现这个选择无法得到期望结果,就回溯回去
使用场景:比如查找二叉树的路径和二叉树的回溯遍历、字符串中字符的所有排列
动态规划
动态规划也是将复杂问题分解成小问题求解的策略,与分治算法不同的是,分治算法要求各子问题是相互独立的,而动态规划各子问题是相互关联的
使用场景:斐波那契数列和爬楼梯问题(爬楼梯问题的解法和斐波那契数列一样)
枚举算法
将问题的所有可能的答案一一列举,然后根据条件判断此答案是否合适,保留合适的,丢弃不合适的
使用场景:长度为n的数组,随机取m个数,有多少种组合
推荐的算法文章
95% 的算法都是基于这 6 种算法思想
前端该如何准备数据结构和算法?[4]
awesome-coding-js 用JS实现的算法和数据结构
从最简单的斐波那契数列来学习动态规划(JavaScript版本)总结
文中列出了现在市面上比较火的一些题目,同时包含了我面试中遇到的所有算法题。算法在阿里、头条、美团的面试中,几乎是必考的。特别是二叉树,我几乎每次都会遇到,为啥大厂对二叉树这么情有独钟? 有知道的小伙伴,麻烦在评论区告诉我,感谢。
如果小伙伴们看了这篇文章后有所收获,那就是我最大的满足
参考资料
[1] 力扣上最长上升子序列的视频讲解:
https://leetcode.cn/problems/longest-increasing-subsequence/solution/shi-pin-tu-jie-zui-chang-shang-sheng-zi-xu-lie-by-/
[2] LeetCode 19.凑零钱问题 动态规划:
https://www.cnblogs.com/Transkai/p/12444261.html
[3] 二叉树在线构建工具:
http://www.easycode.top/binarytree.html
[4] 前端该如何准备数据结构和算法?:
https://juejin.cn/post/6844903919722692621
-
相关阅读:
如何使用ReentrantLock的条件变量,让多个线程顺序执行?
python学习手册
OID的编解码
20. 从零用Rust编写正反向代理,四层反向代理stream(tcp与udp)实现
logback/log4j基本配置和标签详解
基于STM32+微信小程序设计的智能宠物喂养系统_2023升级版
B+树在数据库中的使用
接口优化1
【PTA-训练day14】L2-026 小字辈 + L1-054 福到了
视频加密的误解
- 原文地址:https://blog.csdn.net/lambert00001/article/details/133131463
