-
【李沐深度学习笔记】线性代数实现
课程地址和说明
线性代数实现p2
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
这节就算之前内容的复习,后面以截图形式呈现标量由只有一个元素的张量表示
import torch x = torch.tensor([3.0]) y = torch.tensor([2.0]) # 加减法 print(x+y) # 乘法 print(x * y) # 除法 print(x / y) # 幂运算 print(x**y)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
运行结果:
tensor([5.])
tensor([6.])
tensor([1.5000])
tensor([9.])你可以将向量视为标量值组成的列表
# 生成0-3的顺序列表,(函数是左闭右开) x = torch.arange(4) print(x)- 1
- 2
- 3
运行结果:
tensor([0, 1, 2, 3])通过张量的索引来访问任一元素

访问张量的长度

只有一个轴的张量,形状只有一个元素。

通过指定两个分量m和n来创建一个形状为m × n的矩阵

矩阵的转置
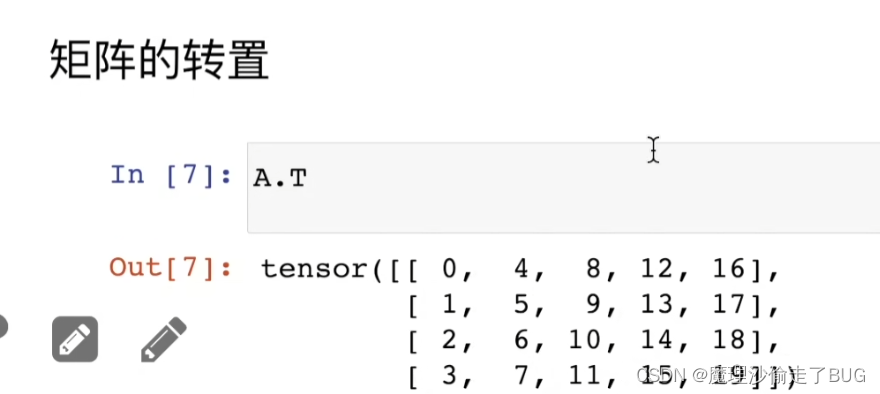
对称矩阵的转置

构造多轴的数据结构

【注】就是构建多维数组给定具有相同形状的任何两个张量,任何按元素二元运算的结果都将是相同形状的张量
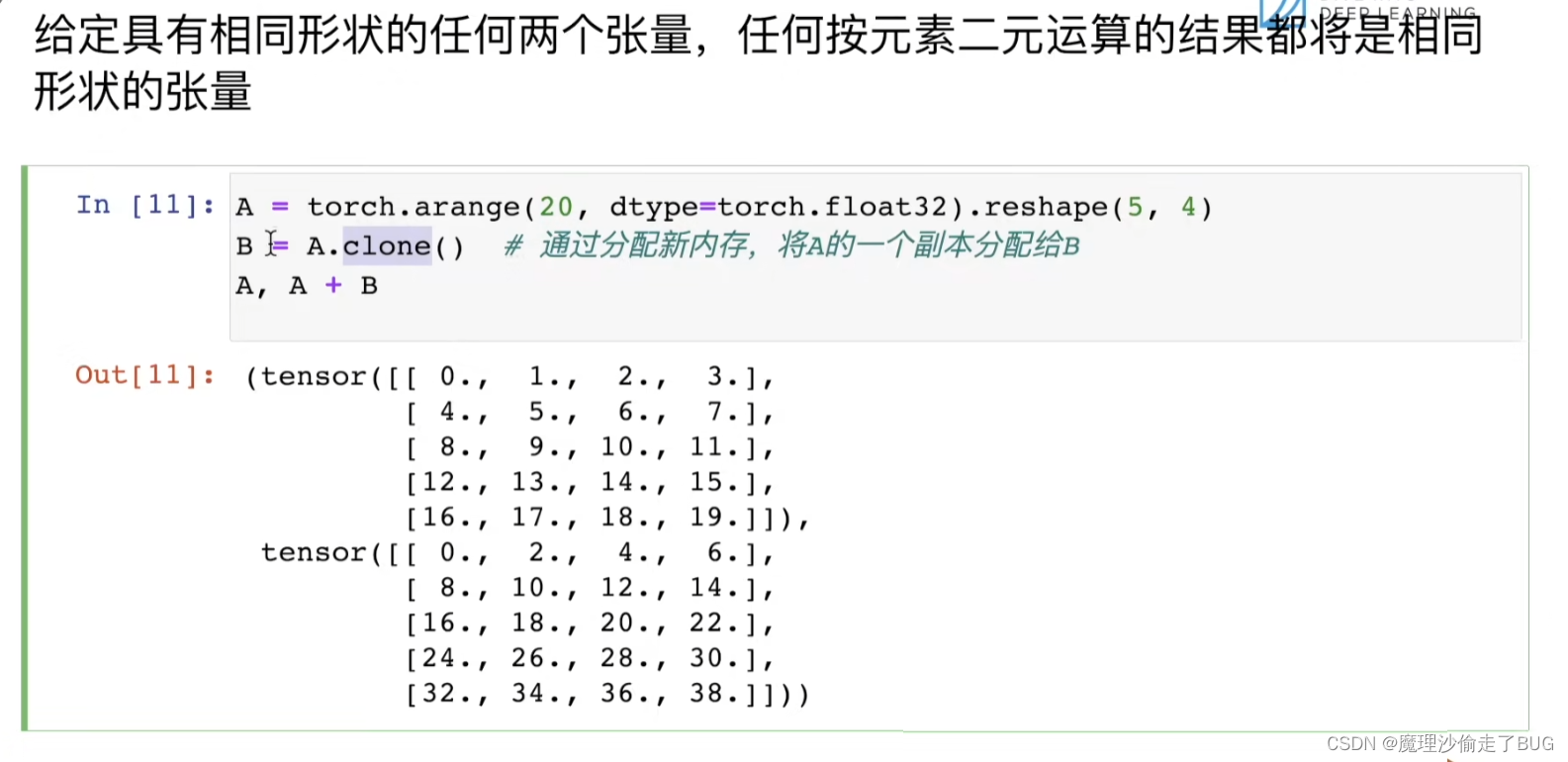
矩阵的哈达玛积
其实就是不按矩阵乘法来,按两个矩阵对应元素相乘得到个新矩阵(前提是矩阵是同形的,即两个相乘的矩阵行列数需要一致)

标量和矩阵相加是所有元素都与标量相加得到新矩阵

计算矩阵所有元素的和

表示任意形状张量的元素和
不论张量形状如何,其求所有元素和的结果永远是标量

指定求和汇总张量的轴(按不同维度求和)

【注】axis是按不同维度求和,从0开始是第1个维度。这里理解上稍微有点难度,我写了代码:# 按维度求和 C = torch.arange(12).reshape(3,4) print(C) # 第一个维度(按列)求和结果 result = C.sum(axis=0) print(result) # 第二个维度(按行)求和结果 result = C.sum(axis=1) print(result) # 对第一和第二维度合并求和 result = C.sum(axis=[0,1]) print(result)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
运行结果:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
tensor([12, 15, 18, 21])
tensor([ 6, 22, 38])
tensor(66)# 按维度求和(三维版) C = torch.arange(27).reshape(3,3,3) print(C) # 第一个维度求和结果 result = C.sum(axis=0) print(result) # 第二个维度求和结果 result = C.sum(axis=1) print(result) # 第三个维度求和结果 result = C.sum(axis=2) print(result) # 对第一和第二维度合并求和 result = C.sum(axis=[0,1]) print(result)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
运行结果:
tensor([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
tensor([[27, 30, 33],
[36, 39, 42],
[45, 48, 51]])
tensor([[ 9, 12, 15],
[36, 39, 42],
[63, 66, 69]])
tensor([[ 3, 12, 21],
[30, 39, 48],
[57, 66, 75]])
tensor([108, 117, 126])
3维版本就相当于这样一个列表,存储了3个矩阵
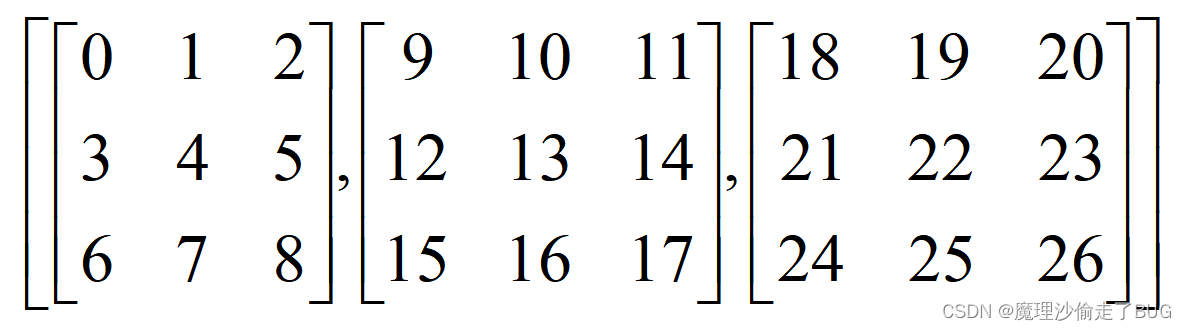
对第一个维度求和,相当于对每一个矩阵按列优先求和,比如第一个矩阵的(1,2)元素和第二个矩阵的(1,2)元素还有第三个矩阵的(1,2)元素相加就是求和结果中的(1,2)元素30。
对第二个维度求和,相当于对每一个矩阵的每一列求和, 然后得到该结果。
对第三个维度求和,对每一个矩阵的行求和,然后得到该结果
对第一个和第二个维度合并求和,相当于先对第一个维度求和,再对得到的二维矩阵的列求和。一个与求和相关的量是平均值(mean或average)

【注】In[20]是指按不同维度求均值计算总和或均值时保持轴数不变
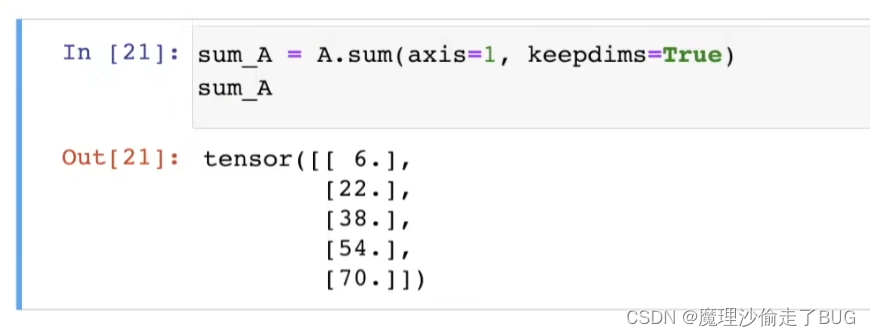
## 不丢维度对各维度求和 a = torch.tensor([[1,2,3],[0,1,2],[0,1,0]]) print(a.sum(axis=0, keepdims=True)) print(a.sum(axis=1, keepdims=True)) ## 最后结果的维度还是2维,和原数据一致- 1
- 2
- 3
- 4
- 5
运行结果:
tensor([[1, 4, 5]])
tensor([[6],
[3],
[1]])通过广播将A除以sum_A
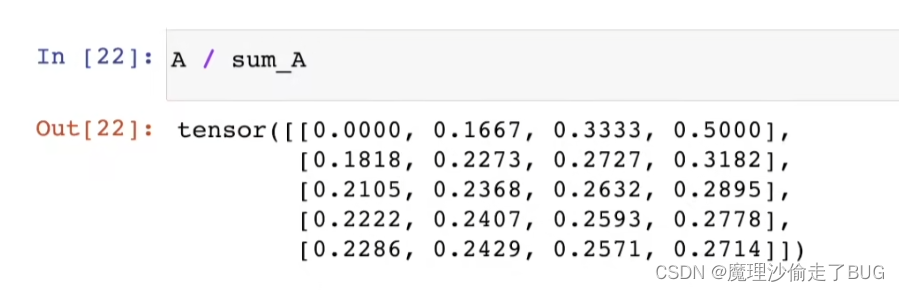
## 接上文的小写a ## 广播机制求均值 ## 用广播机制将求和后的结果补成3X3矩阵再除 print(a) print(a.sum(axis=0, keepdims=True)) print(a / a.sum(axis=0, keepdims=True))- 1
- 2
- 3
- 4
- 5
- 6
运行结果:
tensor([[1, 2, 3],
[0, 1, 2],
[0, 1, 0]])
tensor([[1, 4, 5]])
tensor([[1.0000, 0.5000, 0.6000],
[0.0000, 0.2500, 0.4000],
[0.0000, 0.2500, 0.0000]])某个轴计算A元素的累积总和

# 累加求和 b = torch.arange(12).reshape(3,4) print(b) # 按行累加(即第一行加到第二行变为新的第二行,新的第二行加到第三行变为新的第三行) print(b.cumsum(axis=0)) # 按列累加(即第一列加到第二列变为新的第二列,新的第二列加到第三列变为新的第三列) print(b.cumsum(axis=1))- 1
- 2
- 3
- 4
- 5
- 6
- 7
运行结果:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
tensor([[ 0, 1, 2, 3],
[ 4, 6, 8, 10],
[12, 15, 18, 21]])
tensor([[ 0, 1, 3, 6],
[ 4, 9, 15, 22],
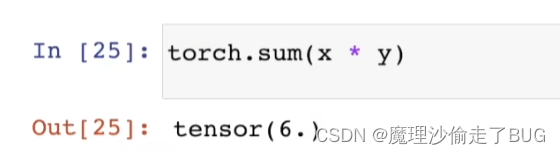
[ 8, 17, 27, 38]])点积是相同位置的按元素乘积的和

我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积
矩阵向量积 A x \bm{A}\bm{x} Ax是一个长度为 m m m的列向量,其 i t h i^{th} ith元素是点积 a i T x a_{i}^{T} \bm{x} aiTx

【注】这里就是想说明 A \bm{A} A是一个 m × n m\times n m×n的矩阵, x \bm{x} x是一个 n × 1 n\times 1 n×1的列向量,其点积结果就是一个 m × 1 m\times 1 m×1的列向量。我们可以将矩阵-矩阵乘法AB看作是简单地执行m次矩阵-向量积,并将结果拼接在一起,形成一个n x m矩阵

【注】a是一个5×3的矩阵。L2范数是向量元素平方和的平方根(欧氏距离)

L范数,它表示为向量元素的绝对值之和

矩阵的弗罗贝尼乌斯范数(Frobenius norm)是矩阵元素的平方和的平方根

-
相关阅读:
基于Docker和MongoDB部署NodeBB论坛系统
Android | ADB 命令
网络安全—综合渗透测试-CVE-2019-15107-Webmin远程代码执行
生产设备上的静电该如何处理?
鸿鹄工程项目管理系统 Spring Cloud+Spring Boot+Mybatis+Vue+ElementUI+前后端分离构建工程项目管理系统项目背景
Pytorch学习——入门知识
Databend 与海外某电信签约:共创海外电信数据仓库新纪元
Java 线程池及线程池状态
分布式锁实现方案-基于zookeeper的分布式锁实现(原理与代码)
pnpm的安装与使用
- 原文地址:https://blog.csdn.net/qq_30204431/article/details/133101807