(并查集) 1971. 寻找图中是否存在路径 ——【Leetcode每日一题】

❓ 1971. 寻找图中是否存在路径

难度：简单

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

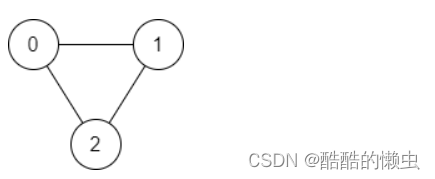
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:

• 0 → 1 → 2
• 0 → 2

示例 2：

输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示：

• $1<=n<=2\ast 10^5$
• $0<=edges.length<=2\ast 10^5$
• $edges[i].length==2$
• $0<=ui,vi<=n-1$
• $ui!=vi$
• $0<=source,destination<=n-1$
• 不存在重复边
• 不存在指向顶点自身的边

💡思路：并查集

们将图中的每个强连通分量视为一个集合，强连通分量中任意两点均可达，如果两个点 source 和 destination 处在同一个强连通分量中，则两点一定可连通，因此连通性问题可以使用并查集解决。

并查集主要有三个功能：

1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个；
2. 将两个节点****接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上；
3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点。

并查集初始化时，n 个顶点分别属于 n 个不同的集合，每个集合只包含一个顶点。初始化之后遍历每条边，由于图中的每条边均为双向边，因此将同一条边连接的两个顶点所在的集合做合并。

遍历所有的边之后，判断顶点 source 和顶点 destination 是否在同一个集合中，如果两个顶点在同一个集合则两个顶点连通，如果两个顶点所在的集合不同则两个顶点不连通。

🍁代码：(C++、Java)

C++

class Solution {
private:
    vector<int> father;

    // 初始化并查集
    void init(int n){
        father = vector<int>(n, 0);
        for(int i = 0; i < n; i++) father[i] = i;
    }

    // 并查集寻根过程
    int find(int u){
        return u == father[u] ? u : father[u] = find(father[u]);
    }

    // 判断 u 和 v 是否找到同一个跟
    bool isSame(int u, int v){
        return find(u) == find(v);
    }

    // 将v->u 这条边加入并查集
    void join(int u, int v){
        u = find(u); // 寻找 u 的根
        v = find(v); // 寻找 v 的根
        if(u == v) return;
        father[u] = v;
    }

public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        if(source == destination) return true;
        init(n);
        for(int i = 0; i < edges.size(); i++){
            join(edges[i][0], edges[i][1]);
        }
        return isSame(source, destination);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

Java

class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        UF uf = new UF(n);
        for(int[] edge :edges) {
            uf.union(edge[0], edge[1]);
        }
        return uf.isConnected(source, destination);
    }

    class UF{
        int[] parent;
        public UF(int n) {
            parent = new int[n];
            for(int i = 0; i < n; i++) parent[i] = i;
        }

        private int find(int x) {
            if(parent[x] == x) return x;
            return parent[x] = find(parent[x]);
        }

        public boolean isConnected(int p, int q) {
            return find(p) == find(q);
        }

        public void union(int p, int q) {
            int pRoot = find(p), qRoot = find(q);
            if(pRoot != qRoot) {
                parent[qRoot] = pRoot;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(n+m\times \alpha (m))$，其中 n 为图中的顶点数，m 是图中边的数目，α 是反阿克曼函数。并查集的初始化需要 $O(n)$的时间，然后遍历 m 条边并执行 m 次合并操作，最后对 source 和 destination 执行一次查询操作，查询与合并的单次操作时间复杂度是 $O(\alpha (m))$，因此合并与查询的时间复杂度是 $O(m\times \alpha (m))$，总时间复杂度是 $O(n+m\times \alpha (m))$。

• 空间复杂度：$O(n)$，其中 n 是图中的顶点数。并查集需要 $O(n)$ 的空间。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！