-
机器学习与模式识别作业1----吸烟者分类
目录
一.题目内容展示
为了解校园内吸烟群体的组成，某高校在校园内随机抽取了10000个大学生（8000个本科生+2000个研究生），并对他们的吸烟情况进行了一个调查。调查结果显示，吸烟的本科生有1200人，吸烟的研究生有400人。(以下填空内容精确到小数点后两位)
二.如果以吸烟/不吸烟为两个类别
Q1： 吸烟者类别的先验概率？不吸烟者类别的先验概率？
Q2： 吸烟者是本科生的类条件概率？不吸烟者是研究生的类条件概率为？
Q3： 已知某学生是本科生，他吸烟的后验概率?
解答:
我们把不吸烟的人设置为
，将吸烟的人设置为
，将本科生设为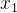
,研究生设为
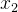。以下题目的答案如下所示:
Q2.1的求解分析
计算两类样本的先验概率，就是取样本在总样本中的占比，如下所示：
Q2.2的求解分析
第一个问题中，已知是吸烟者，求是本科生的类条件概率，如下所示：
" role="presentation" style="position: relative;">
第二个问题中，已知不是吸烟者，求是研究生的类条件概率，如下所示：
Q2.3的求解分析
根据贝叶斯公式，我们能够很快的求解出某学生是本科生，他吸烟的后验概率：
三.如果以本科生/研究生为两个类别
Q1: 已知某学生吸烟，他是本科生的后验概率?
Q2: 已知某学生不吸烟，他是研究生的后验概率为
我们把本科生设置为
，将研究生设置为，将不吸烟者设为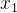,吸烟者设为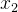。以下题目的答案如下所示:
Q3.1的求解分析
第一个问题中，已知是吸烟者，求是本科生的后验概率，如下所示：
Q3.2的求解分析
第二个问题中，已知是不吸烟者，求是研究生的后验概率，如下所示：
四.题目方法总结
本题旨在熟练使用贝叶斯公式，充分了解类条件概率，先验概率和后验概率的定义，结合题目的数据就能简答快速的求解出来。
-
相关阅读:
基于SSM的校园音乐点歌系统平台
使用 Setter 方法实现 Spring 依赖注入
中宣部防沉迷系统PHP版本(管局防沉迷验证-PHP-全版本-接口测试样例)
git命令提交代码到远程仓库
基于STM32G431嵌入式学习笔记——九、IIC总线（一）EEPROM
健身用什么耳机比较好、五款适合健身房运动的耳机推荐
Android10 SystemUI系列（一）概述
解决 vscode使用Prettier格式化js文件报错：Cannot find module ‘./parser-babylon‘
附近商户-实现附近商户功能
如何备战Shopee大促活动？有什么技巧？
- 原文地址：https://blog.csdn.net/m0_71819746/article/details/133051236