数据结构——二叉搜索树

二叉搜索树是二叉树的一种特殊形式。 二叉搜索树具有以下性质：
1.每个节点中的值必须大于（或等于）其左侧子树中的任何值
2.每个节点中的值必须小于（或等于）其右侧子树中的任何值。

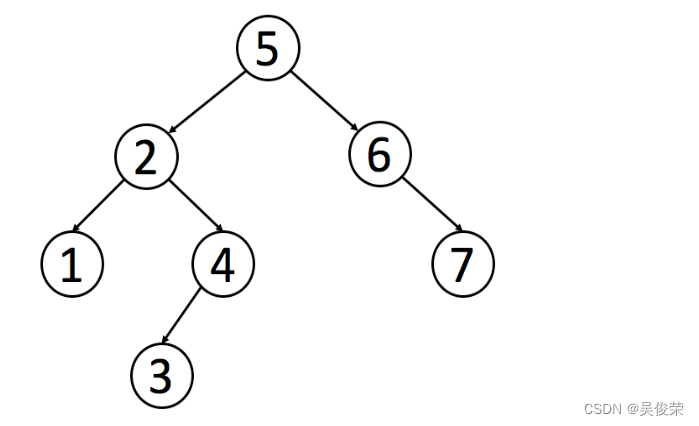
像普通的二叉树一样，我们可以按照前序、中序和后序来遍历一个二叉搜索树。 但是值得注意的是，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。因此，中序遍历是二叉搜索树中最常用的遍历方法。

二叉树搜索：
1.如果目标值等于节点的值，则返回节点；
2.如果目标值小于节点的值，则继续在左子树中搜索；
3.如果目标值大于节点的值，则继续在右子树中搜索。

二叉树插入：
1.根据节点值与目标节点值的关系，搜索左子树或右子树；
2.重复步骤 1 直到到达外部节点；
3.根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

二叉树删除：

1. 如果目标节点没有子节点，我们可以直接移除该目标节点。
2. 如果目标节只有一个子节点，我们可以用其子节点作为替换。
3. 如果目标节点有两个子节点，我们需要用其中序后继节点或者前驱节点来替换，再删除该目标节点。

#include 

// 定义二叉搜索树节点
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class BinarySearchTree {
private:
    TreeNode* root;

    // 插入节点的辅助函数
    TreeNode* insert(TreeNode* node, int val) {
        if (node == nullptr) {
            return new TreeNode(val);
        }

        if (val < node->data) {
            node->left = insert(node->left, val);
        } else if (val > node->data) {
            node->right = insert(node->right, val);
        }

        return node;
    }

    // 中序遍历的辅助函数
    void inorderTraversal(TreeNode* node) {
        if (node == nullptr) {
            return;
        }

        inorderTraversal(node->left);
        std::cout << node->data << " ";
        inorderTraversal(node->right);
    }

    // 查找最小值的辅助函数
    TreeNode* findMin(TreeNode* node) {
        while (node->left != nullptr) {
            node = node->left;
        }
        return node;
    }

    // 删除节点的辅助函数
    TreeNode* remove(TreeNode* node, int val) {
        if (node == nullptr) {
            return node;
        }

        if (val < node->data) {
            node->left = remove(node->left, val);
        } else if (val > node->data) {
            node->right = remove(node->right, val);
        } else {
            if (node->left == nullptr) {
                TreeNode* temp = node->right;
                delete node;
                return temp;
            } else if (node->right == nullptr) {
                TreeNode* temp = node->left;
                delete node;
                return temp;
            }

            TreeNode* temp = findMin(node->right);
            node->data = temp->data;
            node->right = remove(node->right, temp->data);
        }

        return node;
    }

public:
    BinarySearchTree() : root(nullptr) {}

    // 插入节点
    void insert(int val) {
        root = insert(root, val);
    }

    // 搜索节点
    bool search(int val) {
        TreeNode* current = root;
        while (current != nullptr) {
            if (current->data == val) {
                return true;
            } else if (val < current->data) {
                current = current->left;
            } else {
                current = current->right;
            }
        }
        return false;
    }

    // 删除节点
    void remove(int val) {
        root = remove(root, val);
    }

    // 中序遍历
    void inorderTraversal() {
        inorderTraversal(root);
        std::cout << std::endl;
    }
};

int main() {
    BinarySearchTree bst;
    bst.insert(50);
    bst.insert(30);
    bst.insert(70);
    bst.insert(20);
    bst.insert(40);
    bst.insert(60);
    bst.insert(80);

    std::cout << "Inorder Traversal: ";
    bst.inorderTraversal();

    std::cout << "Search 60: " << (bst.search(60) ? "Found" : "Not Found") << std::endl;
    std::cout << "Search 90: " << (bst.search(90) ? "Found" : "Not Found") << std::endl;

    bst.remove(30);
    std::cout << "Inorder Traversal after removing 30: ";
    bst.inorderTraversal();

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135