【八大经典排序算法】选择排序

---

---

一、概述

选择排序作为一种简单直观的排序算法，最早由美国计算机科学家 Donald Knuth 在1968年提出。

选择排序的思想是将数组分为已排序区间和未排序区间，每次从未排序区间中选择最小（或最大）的元素，将其放到已排序区间的末尾，然后缩小未排序区间的范围，直到未排序区间为空。

选择排序的算法复杂度为 O(n^2)，并不是一种高效的排序算法，但它的实现简单，不需要额外的空间，因此对于小规模数组的排序还是比较实用的。

---

二、思路解读

我们知道选择排序是每次从未排序的部分中选择最小（或最大）的元素，然后将其放到已排序部分的末尾，直到所有元素都被排序。(注意：这里是最小（或最大）的元素直接和未排序部分的第一个元素直接交换)
 
所以选择排序实现可以分为以下几步：
①：遍历待排序序列，同时将第一个元素设为最小（或最大）元素。
②：遍历剩余的未排序部分，找到最小（或最大）的元素，并记录其位置。在将最小（或最大）元素与未排序部分的第一个元素交换位置，即将最小（或最大）元素放到已排序部分的末尾。
③：最后重复步骤2和3，直到所有元素都被排序即可。
 
【动画演示】：

---

三、代码实现（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void SelectSort(int* a, int n)
{
	int begin = 0;//未排序的起始下标
	int mini = 0;
	while (begin < n)
	{
		//遍历未排序部分，找到最小值下标
		for (int i = begin; i < n; i++)
		{
			if (a[i] < a[maxi])
			{
				mini = i;
			}
		}
		//最小值和未排序部分的第一个元素交换位置
		Swap(&a[maxi], a[begin]);
		begin++;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

---

四、优化（升序）

我们知道遍历未排序部分时，不仅可以找到最小值，还可以找到最大值。如果我们同时将最大值和最小值的下标同时找出来（以升序为例），在将最小值和未排序部分的首元素交换，最大值和未排序部分的为元素交换。前后同时进行，效率是不是加快了不少呢？
 
但这样有一个易错点，比如：

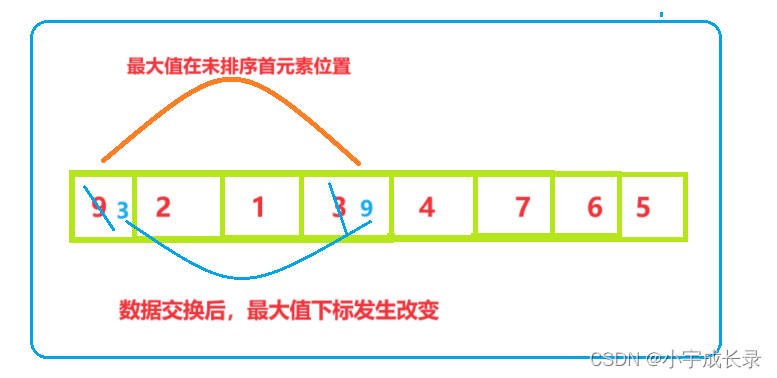
当发生上述极端情况时，我们需要单独处理，更新最大值下标！！
 
【最终代码】：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void  SelectSort(int* a, int n)
{
	int begin = 0;//未排序部分的首元素
	int end = n - 1;//未排序部分的尾元素
	while (begin < end)
	{
		int mini = begin;
		int maxi = begin;
		//遍历未排序部分，找到最(大)小值下标
		for (int i = begin; i <= end; i++)
		{
			if (a[i] > a[maxi])
				maxi = i;
			if (a[i] < a[mini])
				mini = i;
		}
		
		Swap(&a[begin], &a[mini]);
		//最大值下标和未排序首元素下标重合，最大值已经交换到新位置，更新最大值下标
		if (begin == maxi)
			maxi = mini;
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

时间复杂度：O(N^2)
空间复杂度：O(1)