数据结构——红黑树

红黑树（Red-Black Tree）是一种自平衡的二叉查找树，它确保在插入和删除等基本操作后，树保持平衡，从而提供了快速的查找、插入和删除操作。红黑树之所以称为"红黑树"，是因为每个节点都具有一个颜色属性，可以是红色或黑色，它们必须满足一些规则以保持树的平衡性。
性质：
1.树中的任何一个结点都带有颜色, 每个结点的颜色要么是红色, 要么是黑色
2.根结点是黑色
3.所有叶子结点是黑色(在红黑树中, 我们将底层叶结点看做有两个值为 NULL 的孩子结点, 以 NULL 结点作为红黑树的叶结点)
4.每个红色结点的孩子结点一定是黑色
5.对于树中的任意一个结点, 从该结点到所有叶结点的路径上一定包含相同数量的黑结点(我们将红黑树任意结点到叶子结点的路径上的黑色结点的个数称为该结点的 「黑高」)

根据性质得出：
1.没有一条路径比其他路径长出2倍
2.树的高度稳定趋近于log-n
3.一棵有n个节点的红黑树的高度，最多是两倍的2(log(n+1)）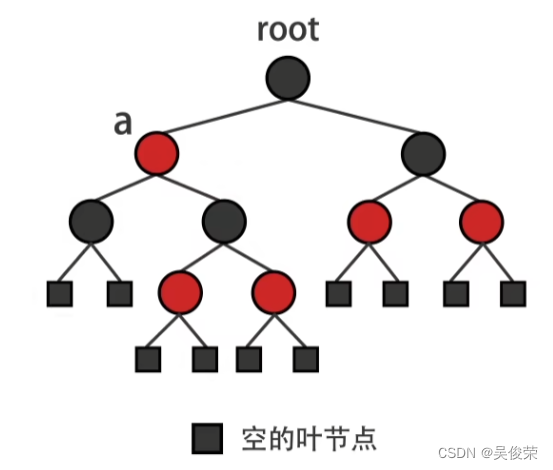

左旋操作（Left Rotation）
左旋是一种将节点向左移动的操作，通常用于修复红黑树的性质。左旋的基本思想是将一个节点的右子节点提升为新的父节点，同时原来的父节点成为新的左子节点。这可以保持二叉搜索树的性质，并且确保红黑树的平衡。

右旋操作（Right Rotation）
右旋是一种将节点向右移动的操作，也用于修复红黑树的性质。右旋的基本思想是将一个节点的左子节点提升为新的父节点，同时原来的父节点成为新的右子节点。这同样可以保持二叉搜索树的性质，并确保红黑树的平衡。

#include 

enum class Color { RED, BLACK };

template <typename T>
struct Node {
    T data;
    Node* parent;
    Node* left;
    Node* right;
    Color color;
};

template <typename T>
class RedBlackTree {
private:
    Node<T>* root;

    // 左旋转
    void leftRotate(Node<T>* x) {
        Node<T>* y = x->right;
        x->right = y->left;
        if (y->left != nullptr) {
            y->left->parent = x;
        }
        y->parent = x->parent;
        if (x->parent == nullptr) {
            root = y;
        } else if (x == x->parent->left) {
            x->parent->left = y;
        } else {
            x->parent->right = y;
        }
        y->left = x;
        x->parent = y;
    }

    // 右旋转
    void rightRotate(Node<T>* y) {
        Node<T>* x = y->left;
        y->left = x->right;
        if (x->right != nullptr) {
            x->right->parent = y;
        }
        x->parent = y->parent;
        if (y->parent == nullptr) {
            root = x;
        } else if (y == y->parent->left) {
            y->parent->left = x;
        } else {
            y->parent->right = x;
        }
        x->right = y;
        y->parent = x;
    }

    // 插入节点修正
    void insertFixup(Node<T>* z) {
        while (z->parent != nullptr && z->parent->color == Color::RED) {
            if (z->parent == z->parent->parent->left) {
                Node<T>* y = z->parent->parent->right;
                if (y != nullptr && y->color == Color::RED) {
                    z->parent->color = Color::BLACK;
                    y->color = Color::BLACK;
                    z->parent->parent->color = Color::RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->right) {
                        z = z->parent;
                        leftRotate(z);
                    }
                    z->parent->color = Color::BLACK;
                    z->parent->parent->color = Color::RED;
                    rightRotate(z->parent->parent);
                }
            } else {
                Node<T>* y = z->parent->parent->left;
                if (y != nullptr && y->color == Color::RED) {
                    z->parent->color = Color::BLACK;
                    y->color = Color::BLACK;
                    z->parent->parent->color = Color::RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->left) {
                        z = z->parent;
                        rightRotate(z);
                    }
                    z->parent->color = Color::BLACK;
                    z->parent->parent->color = Color::RED;
                    leftRotate(z->parent->parent);
                }
            }
        }
        root->color = Color::BLACK;
    }

    // 插入节点
    void insert(Node<T>* z) {
        Node<T>* y = nullptr;
        Node<T>* x = root;
        while (x != nullptr) {
            y = x;
            if (z->data < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }
        z->parent = y;
        if (y == nullptr) {
            root = z;
        } else if (z->data < y->data) {
            y->left = z;
        } else {
            y->right = z;
        }
        z->left = nullptr;
        z->right = nullptr;
        z->color = Color::RED;
        insertFixup(z);
    }

    // 中序遍历
    void inorder(Node<T>* x) {
        if (x != nullptr) {
            inorder(x->left);
            std::cout << x->data << " ";
            inorder(x->right);
        }
    }

public:
    RedBlackTree() : root(nullptr) {}

    // 插入
    void insert(T data) {
        Node<T>* z = new Node<T>;
        z->data = data;
        z->left = nullptr;
        z->right = nullptr;
        z->color = Color::RED;
        insert(z);
    }

    // 中序遍历
    void inorder() {
        inorder(root);
    }
};

int main() {
    RedBlackTree<int> rbTree;
    rbTree.insert(10);
    rbTree.insert(20);
    rbTree.insert(30);
    rbTree.insert(40);
    rbTree.insert(50);
    rbTree.insert(60);
    rbTree.insert(70);

    std::cout << "Inorder Traversal of Red-Black Tree: ";
    rbTree.inorder();
    std::cout << std::endl;

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167