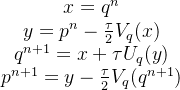• 自洽可分的哈密顿系统的辛算法

    • 本文只介绍哈密顿系统的辛算法的显式结构
      • 不给出具体的推导过程

    自洽可分的哈密顿系统的辛算法

    • 一阶显式辛结构

    \begin{matrix} q^{n+1}=q^n+\tau U_p(p^n) \\ p^{n+1}=p^n-\tau V_q(q^{n+1}) \end{matrix}

    • 二阶显式辛结构

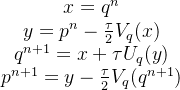
    \begin{matrix} x=q^n\\ y=p^n-\frac{\tau}{2}V_q(x)\\ q^{n+1}=x+\tau U_q(y)\\ p^{n+1}=y-\frac{\tau}{2}V_q(q^{n+1}) \end{matrix}

    • 四阶显式辛结构

    c_1=0,c_2=(2-2^{1/3})^{-1},c_3=1-2(2-2^{1/3}),c_4=(2-2^{1/3})^{-1}

    d_1=d_4=(2-2^{1/3})^{-1},d_2=d_3=(1-(2-2^{1/3})^{-1})/2

    \begin{matrix} x_1=q^n+c_1\tau U_p(p^n) &y_1 = p^n -d_1V_q(x_1) \\ x_2=x_1+c_2\tau U_p(y_1) & y_2 =y_1-d_2\tau V_q(x_2)\\ x_3 = x_2 + c_3\tau U_p(y_2) &y_3=y_2 -d_3\tau V_q(x_3) \\ q^{n+1}=x_3 +c_4\tau U_p(y_3) &p^{n+1}=y_3-d_4\tau V_q(q^{n+1}) \end{matrix}

    • 全代码
    1. import matplotlib.pyplot as plt
    2. import numpy as np
    3. from scipy.optimize import fsolve
    4.  
    5. ##SymplecticHamilton
    6. ##self-consistent
    7. ##separable
    8. class symhamcssolver():
    9.  
    10.     def __init__(self, Up, Vq, 
    11.                  q0=np.array([0]),
    12.                  p0=np.array([1]), 
    13.                  T_start=0, T_end=20, tau=0.01):
    14.  
    15.  
    16.         self.Up = Up
    17.         self.Vq = Vq
    18.  
    19.         self.tau = tau
    20.         self.T = np.arange(T_start, T_end, self.tau)
    21.         self.size = len(self.T)
    22.  
    23.         self.q = np.zeros((len(self.T), len(q0)))
    24.         self.q[0, :] = q0
    25.  
    26.         self.p = np.zeros((len(self.T), len(p0)))
    27.         self.p[0, :] = p0
    28.         
    29.         self.tol = 1e-6
    30.  
    31.     def __str__(self):
    32.         return f"Symplectic algrithm of self-consistent and separable Hamilton system"
    33.  
    34.  
    35.     def E1(self,):
    36.         for i in range(1, self.size):
    37.             self.q[i, :] = self.q[i-1, :] + self.tau * self.Up(self.p[i-1, :])
    38.             self.p[i, :] = self.p[i-1, :] - self.tau * self.Vq(self.q[i, :])
    39.         return self.p, self.q
    40.     
    41.     def E2(self,):
    42.         for i in range(1, self.size):
    43.             x = self.q[i-1, :]
    44.             y = self.p[i-1, :] - self.tau/2 * self.Vq(x)
    45.             self.q[i, :] = x + self.tau * self.Up(y)
    46.             self.p[i, :] = y - self.tau/2 * self.Vq(self.q[i, :])
    47.         return self.p, self.q
    48.  
    49.     def E4(self,):
    50.         alpha = 1/(2-2**(1/3))
    51.         beta  = 1 - 2 * alpha
    52.         c = np.zeros(5)
    53.         d = np.zeros(5)
    54.         c[2] = alpha
    55.         c[4] = alpha
    56.         c[3] = beta
    57.         d[1] = alpha/2
    58.         d[4] = alpha/2
    59.         d[2] = (alpha + beta)/2
    60.         d[3] = (alpha + beta)/2
    61.  
    62.         for i in range(1, self.size):
    63.             x1 = self.q[i-1, :] + c[1] * self.tau * self.Up(self.p[i-1, :])
    64.             y1 = self.p[i-1, :] - d[1] * self.tau * self.Vq(x1)
    65.             x2 = x1 + c[2] * self.tau * self.Up(y1)
    66.             y2 = y1 - d[2] * self.tau * self.Vq(x2)
    67.             x3 = x2 + c[3] * self.tau * self.Up(y2)
    68.             y3 = y2 - d[3] * self.tau * self.Vq(x3)
    69.             self.q[i, :] = x3 + c[4] * self.tau * self.Up(y3)
    70.             self.p[i, :] = y3 - d[4] * self.tau * self.Vq(self.q[i, :])
    71.  
    72.         return self.p, self.q
    73.  
    74.  
    75. ## H = p^2/2m + k/2q^2
    76. m = 1
    77. k = 1
    78. Up = lambda p:p[:]/m
    79. Vq = lambda q:k*q[:]
    80.     
    81. c = symhamcssolver(Up, Vq)
    82.  
    83. fig = plt.figure(figsize=(12, 4))
    84. ax1 = fig.add_subplot(1,3,1)
    85. ax2 = fig.add_subplot(1,3,2)
    86. ax3 = fig.add_subplot(1,3,3)
    87.  
    88. p, q = c.E1()
    89. ax1.plot(p, q)
    90. ax1.set_title("E1")
    91. ax1.set_xlabel("q")
    92. ax1.set_ylabel("p", rotation=0)
    93.  
    94. p, q = c.E2()
    95. ax2.plot(p, q)
    96. ax2.set_title("E2")
    97. ax2.set_xlabel("q")
    98. ax2.set_ylabel("p", rotation=0) 
    99.  
    100. p, q = c.E4()
    101. ax3.plot(p, q)
    102. ax3.set_title("E4")
    103. ax3.set_xlabel("q")
    104. ax3.set_ylabel("p", rotation=0)
    105.  
    106. plt.pause(0.01)
    107.  
    108.  
    109.  
    110.

    • 解示意图 

     

    含时可分哈密顿系统

    1. import matplotlib.pyplot as plt
    2. import numpy as np
    3. from scipy.optimize import fsolve
    4.  
    5. ##SymplecticHamilton
    6. ##self-inconsistent
    7. ##separable
    8.  
    9. ##
    10. ## \frac{dq}{dt} =  U_p(p, t)
    11. ## \frac{dp}{dt} = -V_q(q, t)
    12.  
    13. ##
    14. class symhamicssolver():
    15.  
    16.     def __init__(self, Up, Vq, 
    17.                  q0=np.array([0]),
    18.                  p0=np.array([1]), 
    19.                  T_start=0, T_end=20, tau=0.01):
    20.  
    21.         self.Up = Up
    22.         self.Vq = Vq
    23.  
    24.         self.tau = tau
    25.         self.T = np.arange(T_start, T_end, self.tau)
    26.         self.size = len(self.T)
    27.  
    28.         self.q = np.zeros((len(self.T), len(q0)))
    29.         self.q[0, :] = q0
    30.  
    31.         self.p = np.zeros((len(self.T), len(p0)))
    32.         self.p[0, :] = p0
    33.         
    34.         self.tol = 1e-6
    35.  
    36.     def __str__(self):
    37.         return f"Symplectic algrithm of self-inconsistent and separable Hamilton system"
    38.  
    39.     def E1(self,):
    40.         for i in range(1, self.size):
    41.             self.q[i, :] = self.q[i-1, :] + self.tau * self.Up(self.p[i-1, :], self.T[i-1])
    42.             self.p[i, :] = self.p[i-1, :] - self.tau * self.Vq(self.q[i, :]  , self.T[i])
    43.         return self.p, self.q
    44.     
    45.     def E2(self,):
    46.         for i in range(1, self.size):
    47.             x = self.q[i-1, :]
    48.             y = self.p[i-1, :] - self.tau/2 * self.Vq(x, self.T[i-1])
    49.             self.q[i, :] = x + self.tau * self.Up(y, self.T[i-1]+self.tau/2)
    50.             self.p[i, :] = y - self.tau/2 * self.Vq(self.q[i, :], self.T[i])
    51.         return self.p, self.q
    52.  
    53.     def E4(self,):
    54.         alpha = 1/(2-2**(1/3))
    55.         beta  = 1 - 2 * alpha
    56.         c = np.zeros(5)
    57.         d = np.zeros(5)
    58.         c[2] = alpha
    59.         c[4] = alpha
    60.         c[3] = beta
    61.         d[1] = alpha/2
    62.         d[4] = alpha/2
    63.         d[2] = (alpha + beta)/2
    64.         d[3] = (alpha + beta)/2
    65.  
    66.         for i in range(1, self.size):
    67.             x1 = self.q[i-1, :] + c[1] * self.tau * self.Up(self.p[i-1, :], self.T[i])
    68.             zeta1 = self.T[i-1] + c[1] * self.tau
    69.             y1 = self.p[i-1, :] - d[1] * self.tau * self.Vq(x1, zeta1)
    70.             eta1  = self.T[i-1] + d[1] * self.tau
    71.             
    72.             x2 = x1 + c[2] * self.tau * self.Up(y1, eta1)
    73.             zeta2 = zeta1 + c[2] * self.tau
    74.             y2 = y1 - d[2] * self.tau * self.Vq(x2, zeta2)
    75.             eta2  = eta1 + d[2] * self.tau             
    76.             
    77.             x3 = x2 + c[3] * self.tau * self.Up(y2, eta2)
    78.             zeta3 = zeta2 + c[3] * self.tau
    79.             y3 = y2 - d[3] * self.tau * self.Vq(x3, zeta3)
    80.             eta3  = eta2 + d[3] * self.tau
    81.             
    82.             self.q[i, :] = x3 + c[4] * self.tau * self.Up(y3, eta3)
    83.             self.p[i, :] = y3 - d[4] * self.tau * self.Vq(self.q[i, :], self.T[i])
    84.  
    85.         return self.p, self.q
    86.  
    87.  
    88. ## H = p^2/2m + k/2q^2
    89. m = 1
    90. k = 1
    91. Up = lambda p, t:p[:]/m + t
    92. Vq = lambda q, t:k*q[:] + t
    93.     
    94. c = symhamicssolver(Up, Vq)
    95.  
    96. fig = plt.figure(figsize=(12, 4))
    97. ax1 = fig.add_subplot(1,3,1)
    98. ax2 = fig.add_subplot(1,3,2)
    99. ax3 = fig.add_subplot(1,3,3)
    100.  
    101. p, q = c.E1()
    102. ax1.plot(p, q)
    103. ax1.set_title("E1")
    104. ax1.set_xlabel("q")
    105. ax1.set_ylabel("p", rotation=0)
    106.  
    107. p, q = c.E2()
    108. ax2.plot(p, q)
    109. ax2.set_title("E2")
    110. ax2.set_xlabel("q")
    111. ax2.set_ylabel("p", rotation=0) 
    112.  
    113. p, q = c.E4()
    114. ax3.plot(p, q)
    115. ax3.set_title("E4")
    116. ax3.set_xlabel("q")
    117. ax3.set_ylabel("p", rotation=0)
    118.  
    119. plt.pause(0.01)
    120.  
    121.  
    122.  
    123.

  • 相关阅读:
    结合CAP理论分析ElasticSearch的分布式实现方式
    Bigkey问题的解决思路与方式探索
    Unity Shader入门精要学习——透明效果
    springboot一个简单的前端响应后端查询项目
    JAVA餐饮掌上设备点餐系统计算机毕业设计Mybatis+系统+数据库+调试部署
    RobotFramework用户关键字（一）
    Python 中的后台进程
    【构建ML驱动的应用程序】第 11 章 ：监控和更新模型
    太赞了！美团T9大牛硬肝仨月总结出Linux高性能服务器编程
    差分约束原理及其应用
  • 原文地址：https://blog.csdn.net/Chandler_river/article/details/132972957