【深度学习实验】线性模型（三）：使用Pytorch实现简单线性模型：搭建、构造损失函数、计算损失值

目录

一、实验介绍

 二、实验环境

1. 配置虚拟环境

2. 库版本介绍

三、实验内容

0. 导入库

1. 定义线性模型linear_model

2. 定义损失函数loss_function

3. 定义数据

4. 调用模型

5. 完整代码

---

 

 

一、实验介绍

• 使用Pytorch实现
  • 线性模型搭建
  • 构造损失函数
  • 计算损失值

 

 二、实验环境

        本系列实验使用了PyTorch深度学习框架，相关操作如下：

1. 配置虚拟环境

conda create -n DL python=3.7 

conda activate DL

pip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html

conda install matplotlib

 conda install scikit-learn

2. 库版本介绍

 

三、实验内容

ChatGPT：

 

        线性模型是一种基本的机器学习模型，用于建立输入特征与输出之间的线性关系。它是一种线性组合模型，通过对输入特征进行加权求和，再加上一个偏置项，来预测输出值。

        线性模型的一般形式可以表示为：y = w1x1 + w2x2 + ... + wnxn + b，其中y是输出变量，x1, x2, ..., xn是输入特征，w1, w2, ..., wn是特征的权重，b是偏置项。模型的目标是通过调整权重和偏置项，使预测值与真实值之间的差异最小化。

线性模型有几种常见的应用形式：

1. 线性回归（Linear Regression）：用于建立输入特征与连续输出之间的线性关系。它通过最小化预测值与真实值的平方差来拟合最佳的回归直线。

2. 逻辑回归（Logistic Regression）：用于建立输入特征与二分类或多分类输出之间的线性关系。它通过使用逻辑函数（如sigmoid函数）将线性组合的结果映射到概率值，从而进行分类预测。

3. 支持向量机（Support Vector Machines，SVM）：用于二分类和多分类问题。SVM通过找到一个最优的超平面，将不同类别的样本分隔开。它可以使用不同的核函数来处理非线性问题。

4. 岭回归（Ridge Regression）和Lasso回归（Lasso Regression）：用于处理具有多重共线性（multicollinearity）的回归问题。它们通过对权重引入正则化项，可以减小特征的影响，提高模型的泛化能力。

        线性模型的优点包括简单、易于解释和计算效率高。它们在许多实际问题中都有广泛的应用。然而，线性模型也有一些限制，例如对非线性关系的建模能力较弱。在处理复杂的问题时，可以通过引入非线性特征转换或使用核函数进行扩展，以提高线性模型的性能。

本系列为实验内容，对理论知识不进行详细阐释

（咳咳，其实是没时间整理，待有缘之时，回来填坑）

 

0. 导入库

import torch

 

1. 定义线性模型linear_model

        该函数接受输入数据x，使用随机生成的权重w和偏置b，计算输出值output。这里的线性模型的形式为 output = x * w + b。

def linear_model(x):
    w = torch.rand(1, 1, requires_grad=True)
    b = torch.randn(1, requires_grad=True)
    return torch.matmul(x, w) + b

 

2. 定义损失函数loss_function

      这里使用的是均方误差（MSE）作为损失函数，计算预测值与真实值之间的差的平方。

def loss_function(y_true, y_pred):
    loss = (y_pred - y_true) ** 2
    return loss

 

3. 定义数据

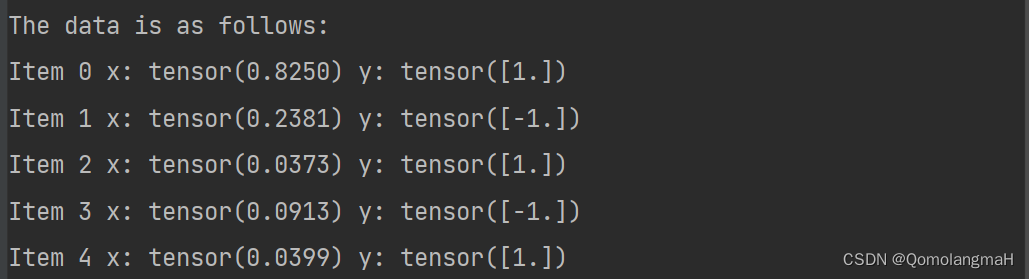
• 生成一个随机的输入张量 x，形状为 (5, 1)，表示有 5 个样本，每个样本的特征维度为 1。

• 生成一个目标张量 y，形状为 (5, 1)，表示对应的真实标签。

• 打印数据的信息，包括每个样本的输入值x和目标值y。

x = torch.rand(5, 1)
y = torch.tensor([1, -1, 1, -1, 1], dtype=torch.float32).view(-1, 1)
print("The data is as follows:")
for i in range(x.shape[0]):
    print("Item " + str(i), "x:", x[i][0], "y:", y[i])

 

4. 调用模型

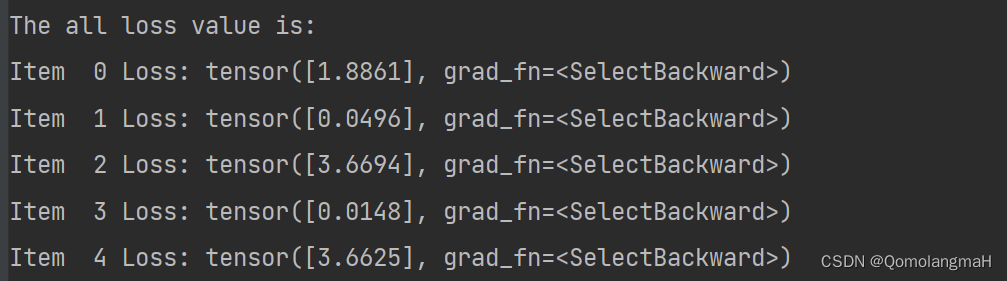
• 使用 linear_model 函数对输入 x 进行预测，得到预测结果 prediction。

• 使用 loss_function 计算预测结果与真实标签之间的损失，得到损失张量 loss。

• 打印了每个样本的损失值。

prediction = linear_model(x)
loss = loss_function(y, prediction)
print("The all loss value is:")
for i in range(len(loss)):
    print("Item ", str(i), "Loss:", loss[i])

 

 

5. 完整代码

import torch
 
def linear_model(x):
    w = torch.rand(1, 1, requires_grad=True)
    b = torch.randn(1, requires_grad=True)
    return torch.matmul(x, w) + b
 
def loss_function(y_true, y_pred):
    loss = (y_pred - y_true) ** 2
    return loss
 
x = torch.rand(5, 1)
y = torch.tensor([1, -1, 1, -1, 1], dtype=torch.float32).view(-1, 1)
print("The data is as follows:")
for i in range(x.shape[0]):
    print("Item " + str(i), "x:", x[i][0], "y:", y[i])
 
prediction = linear_model(x)
loss = loss_function(y, prediction)
print("The all loss value is:")
for i in range(len(loss)):
    print("Item ", str(i), "Loss:", loss[i])

 

注意：

        本实验的线性模型仅简单地使用随机权重和偏置，计算了模型在训练集上的均方误差损失，没有使用优化算法进行模型参数的更新。

        通常情况下会使用梯度下降等优化算法来最小化损失函数，并根据训练数据不断更新模型的参数，具体内容请听下回分解。