【算法与数据结构】538、LeetCode把二叉搜索树转换为累加树

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

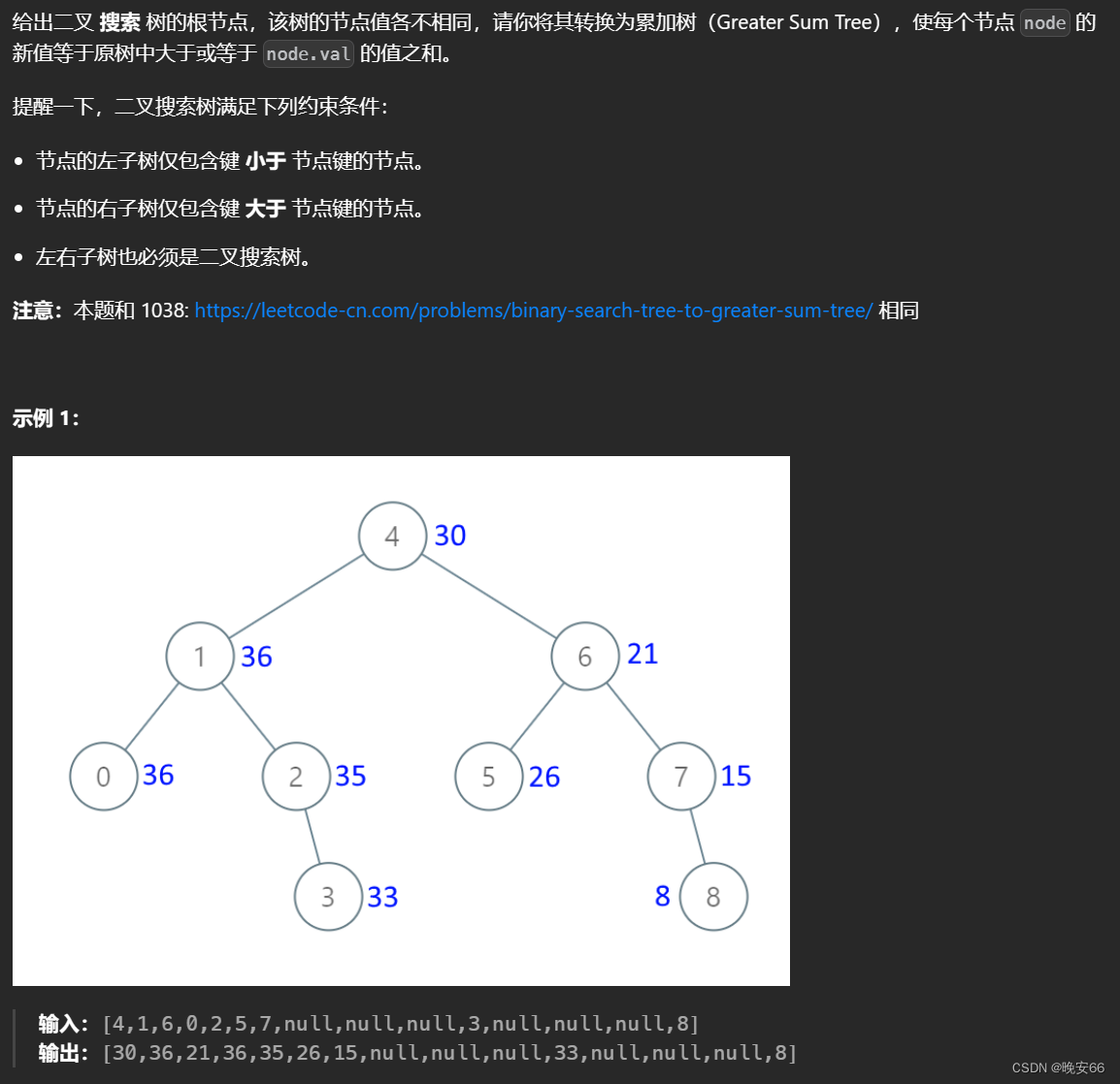
二、两个解法

  思路分析：本题笔者想了一个很笨的方法，遍历的两次二叉树，依次用来记录二叉树的值，另一次用来修改二叉树的值。首先我们先遍历一次，将二叉搜索树的值存放在数组当中，然后再次遍历，用累加求和，修改二叉树的值。
  程序如下：

class Solution {
public:
    void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder(cur->left, vec);     // 左
        vec.push_back(cur->val);                // 中
        traversal_midOrder(cur->right, vec);    // 右
    }
    void traversal_midOrder_sum(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder_sum(cur->left, vec);     // 左
        int sum = 0;
        for (int i = 0; i < vec.size(); i++) {  // 中           
            if (vec[i] >= cur->val) {
                sum += vec[i];
            }
        }
        cur->val = sum;
        traversal_midOrder_sum(cur->right, vec);    // 右
    }
    // 中序遍历得到有序数组，然后再次中序遍历，加上对应值
    TreeNode* convertBST(TreeNode* root) {
        vector<int> v;
        traversal_midOrder(root, v);
        traversal_midOrder_sum(root, v);
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

复杂度分析：

• 时间复杂度： $O(n)$，遍历两次，$O(2n)=O(n)$。
• 空间复杂度：$O(n)$。

  思路分析：经过一番思索，二叉搜索树的中序遍历时一个有序数组，累加实际上是把后序遍历数组中大于等于节点键值的值累加，然后重新赋值给节点。实际上这种累加就是后序累加，[1, 2, 3]变成[6, 5, 3]。那么我们用右中左这种反中序遍历的方式遍历二叉搜索树。程序还是用递归实现，反后序遍历会先找到最大的那个节点(最大节点的累计值等于本身，因此pre初始化为0)，然后令当前节点加上上一个节点的值，更新pre，反复递归。
  程序如下：

class Solution2 {
private:
    int pre = 0; // 记录前一个节点的数值
    void traversal(TreeNode* cur) { // 右中左遍历
        if (cur == NULL) return;
        traversal(cur->right);
        cur->val += pre;
        pre = cur->val;
        traversal(cur->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

复杂度分析：

• 时间复杂度： $O(n)$，遍历一次。
• 空间复杂度：$O(n)$。

三、完整代码

# include 
# include 
# include 
# include 
using namespace std;

// 树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder(cur->left, vec);     // 左
        vec.push_back(cur->val);                // 中
        traversal_midOrder(cur->right, vec);    // 右
    }
    void traversal_midOrder_sum(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder_sum(cur->left, vec);     // 左
        int sum = 0;
        for (int i = 0; i < vec.size(); i++) {  // 中           
            if (vec[i] >= cur->val) {
                sum += vec[i];
            }
        }
        cur->val = sum;
        traversal_midOrder_sum(cur->right, vec);    // 右
    }
    // 中序遍历得到有序数组，然后再次中序遍历，加上对应值
    TreeNode* convertBST(TreeNode* root) {
        vector<int> v;
        traversal_midOrder(root, v);
        traversal_midOrder_sum(root, v);
        return root;
    }
};

class Solution2 {
private:
    int pre = 0; // 记录前一个节点的数值
    void traversal(TreeNode* cur) { // 右中左遍历
        if (cur == NULL) return;
        traversal(cur->right);
        cur->val += pre;
        pre = cur->val;
        traversal(cur->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};

// 前序遍历迭代法创建二叉树，每次迭代将容器首元素弹出（弹出代码还可以再优化）
void Tree_Generator(vector<string>& t, TreeNode*& node) {
    if (!t.size() || t[0] == "NULL") return;    // 退出条件
    else {
        node = new TreeNode(stoi(t[0].c_str()));    // 中
        if (t.size()) {
            t.assign(t.begin() + 1, t.end());
            Tree_Generator(t, node->left);              // 左
        }
        if (t.size()) {
            t.assign(t.begin() + 1, t.end());
            Tree_Generator(t, node->right);             // 右
        }
    }
}

template<typename T>
void my_print(T& v, const string msg)
{
    cout << msg << endl;
    for (class T::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << ' ';
    }
    cout << endl;
}

template<class T1, class T2>
void my_print2(T1& v, const string str) {
    cout << str << endl;
    for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {
        for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {
            cout << *it << ' ';
        }
        cout << endl;
    }
}

// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();  // size必须固定, que.size()是不断变化的
        vector<int> vec;
        for (int i = 0; i < size; ++i) {
            TreeNode* node = que.front();
            que.pop();
            vec.push_back(node->val);
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
        result.push_back(vec);
    }
    return result;
}

int main()
{
    // 构建二叉树
    vector<string> t = { "4", "1", "0", "NULL", "NULL", "2", "NULL", "3", "NULL", "NULL", "6", "5", "NULL", "NULL", "7", "NULL", "8", "NULL", "NULL" };   // 前序遍历
    my_print(t, "目标树");
    TreeNode* root = new TreeNode();
    Tree_Generator(t, root);
    vector<vector<int>> tree = levelOrder(root);
    my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:");

    // 转化为累加树目标值
    Solution s;
    TreeNode* result = s.convertBST(root);
    vector<vector<int>> tree1 = levelOrder(result);
    my_print2<vector<vector<int>>, vector<int>>(tree1, "结果树:");

    system("pause");
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139

end