最小二乘法

1、相关的矩阵公式

P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ = A T i i : σ ξ T A ξ σ ξ = A T ξ + A ξ i i i : ( A B ) T = B T A T i v : ( A + B ) T = A T + B T v : ∥ ξ ∥ = ξ T ξ Precondition:ξ∈Rn,A∈Rn∗ni:σAξσξ=ATii:σξTAξσξ=ATξ+Aξiii:(AB)T=BTATiv:(A+B)T=AT+BTv:‖ξ‖=ξTξ

Precondition:ξ∈Rn,A∈Rn∗ni:σξσAξ​=ATii:σξσξTAξ​=ATξ+Aξiii:(AB)T=BTATiv:(A+B)T=AT+BTv:∥ξ∥=ξTξ​

2、线性回归

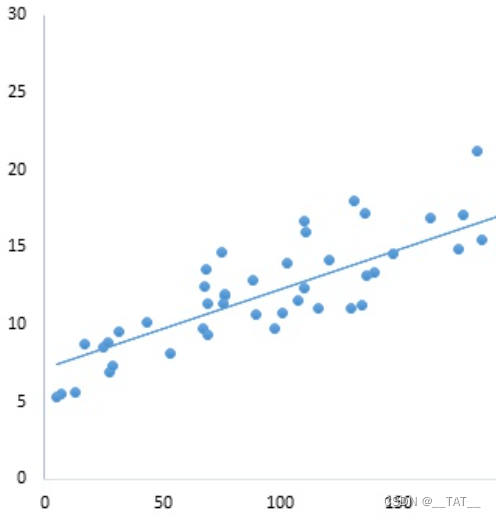
线性回归（Linear Regression）个人理解大概是说，一组数据基本上服从线性分布。举一个在二维平面中线性回归的例子，如下图所示，我们可以找到一条表达式为$y=ax+b$的直线来大概的拟合这些数据。进而，我们可以用这条直线去预测新输入的点的相应的坐标。那么这种寻找线性方程去拟合数据的方式我们称之为线性回归。

3、最小二乘法

3.1、损失函数（Loss Function）

在二维平面中，我们可以设这条可以拟合大多数数据的直线的表达式如下:
$$h\left(\theta \right)={\theta }_{1}x+{\theta }_2$$
其中${\theta }_1$和${\theta }_2$就是$y=ax+b$中的$a$和$b$，只是换了一种表达而已。
接着，可以求得平面上每一个点在这条直线上对应的坐标（即估计值）：
h 1 ( θ ) = θ 1 x 1 + θ 2 h 2 ( θ ) = θ 1 x 2 + θ 2 . . . . h n ( θ ) = θ 1 x n + θ 2 h1(θ)=θ1x1+θ2h2(θ)=θ1x2+θ2....hn(θ)=θ1xn+θ2

h1​(θ)=θ1​x1​+θ2​h2​(θ)=θ1​x2​+θ2​....hn​(θ)=θ1​xn​+θ2​​

再求这些点在直线上的坐标和真实坐标的差的平方，就得到损失函数的表达式。
$$L\left(\theta \right)=\sum _{i=1}^m{\left(h_i\left(\theta \right)-f\left(x_i\right)\right)}^2$$
其中$f\left(x_i\right)$则是$x_i$对应的真实坐标值。
因此，可以通过损失函数$L\left(\theta \right)$来找出适当的${\theta }_1$和${\theta }_2$，使其$f\left(x_i\right)$之间的方差最小。求解方法放在后面讲。

3.2、多维空间的损失函数

在$m$维线性空间中，有$n$个点。其对应的预测方程应该如下：

h 1 ( θ ) = θ 1 x 11 + θ 2 x 12 + . . . + θ m − 1 x 1 m − 1 + θ m h 2 ( θ ) = θ 1 x 21 + θ 2 x 22 + . . . + θ m − 1 x 2 m − 1 + θ m . . . h n ( θ ) = θ 1 x n 1 + θ 2 x n 2 + . . . + θ m − 1 x n m − 1 + θ m h1(θ)=θ1x11+θ2x12+...+θm−1x1m−1+θmh2(θ)=θ1x21+θ2x22+...+θm−1x2m−1+θm...hn(θ)=θ1xn1+θ2xn2+...+θm−1xnm−1+θm

h1​(θ)=θ1​x11​+θ2​x12​+...+θm−1​x1m−1​+θm​h2​(θ)=θ1​x21​+θ2​x22​+...+θm−1​x2m−1​+θm​...hn​(θ)=θ1​xn1​+θ2​xn2​+...+θm−1​xnm−1​+θm​​
其中$n>m$（方程数量等比未知数多才能有解）。损失函数的表达式依旧如此：
$$L\left(\theta \right)=\sum _{i=1}^m{\left(h_i\left(\theta \right)-f\left(x_i\right)\right)}^2$$
那么再将以上的所有变量矩阵化：

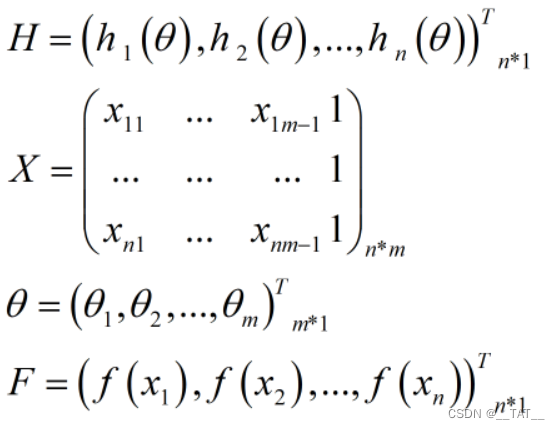
可以得到损失函数的表达式为：
$$L\left(\theta \right)={\Vert X\theta -F\Vert }^2={\left(X\theta -F\right)}^T\left(X\theta -F\right)$$
再展开化简：
$$\begin{array}{l}L\left(\theta \right)={\Vert X\theta -F\Vert }^2={\left(X\theta -F\right)}^T\left(X\theta -F\right)\\ \\ =\left({\theta }^T{X}^T-F^T\right)\left(X\theta -F\right)={\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}F-F^{T}X\theta +F^{T}F\\ \\ ={\theta }^T{X}^{T}X\theta -2F^{T}X\theta +F^{T}F\end{array}$$
根据上文，我们知道化简的目的是为了找到适当的$\theta$使得损失函数$L\left(\theta \right)$最小，而常用的求$\theta$有两种，分别是解析法求解和梯度下降法。

3.3、解析法求解

从高数可以知，当偏导等于零时，该点是极值点（说的不严谨emm）。所以我们直接求偏导，另其为零即可得$\theta$。
σ L ( θ ) σ θ = 2 X T X θ − 2 X T F = 0 θ = ( X T X ) − 1 X T F σL(θ)σθ=2XTXθ−2XTF=0θ=(XTX)−1XTF

σθσL(θ)​=2XTXθ−2XTF=0θ=(XTX)−1XTF​
但这种方法要求$X^{T}X$是可逆的，即行列式不为零or满秩。很多时候这个条件并不成立，所以在机器学习(Machine Learning)中经常用到梯度下降法。

3.4、梯度下降法求解

梯度下降基本思想是先随便取一个${\theta }_i$，然后带入下式看看损失函数多大，然后再在${\theta }_i$基础上，取一个稍微小一点或大一点的${\theta }_j$带入下式，看看此时的损失函数多大。如此往复，找到那个最优的$\theta$的取值。
$$L\left({\theta }_{\mathrm{i}}\right)={{\theta }_i}^T{X}^{T}X{\theta }_i-2F^{T}X{\theta }_i+F^{T}F$$