-
基于Y向连贯性算法的多边形扫描线生成(适用于凸多边形和凹多边形)【原理+java实现】
问题介绍
给定一个多边形,可能是凸多边形,也可能是凹多边形,现需要生成一系列线条将多边形描述出来,示例如下图

原始方法
遇到这个问题,大家首先想到的方法可能是:使用一系列的竖线来和多边形进行相交,得到几个交点,然后将交点按照z轴坐标值进行升序排序,最后再以两个点为一组来形成扫描线。这样确实很容易理解,但是性能不好,因为需要多次求交点和多次对交点进行排序
Y向连贯性算法
该算法主要就是用来解决上面提到的两个性能问题:多次求交点及多次排序。
避免多次求交点
如何避免多次求交点呢?其实非常简单,就是利用直线函数 y=kx+b 的信息即可,例如x每增加1,y就增加 k 。如下面的例子,假如一开始就知道P点的坐标,那么线段与扫描线1、扫描线2的交点并不需要再去用直线相交公式计算,直接使用 y=kx+b 即可得到

如何避免多次排序
如下图所示,当扫描线在x=[0,10]之间移动时,永远只有上下两个交点,且P2永远在P1上面,那只要x在[0,10]之间移动时,只需要根据直线的表达式来对两个点的坐标进行更新即可,不需要排序两个点。当x>10之后,有新的边和扫描线相交,这时候会出现更多的交点,此时才需要对交点进行排序,大大减少了排序的次数

如何实现
首先需要维护一个边表,遍历多边形的每一条边,将边放到对应的桶中;第二步就是维护一个有效边集合,将y开始向右扫描移动,y的初始值是多边形所有点中最小的那个y,在移动的过程中,主要做一下三件事:
- 是否有边失效?当扫描线扫描不到时,边就失效,将其从有效边集合中移除
- 是否有新的有效边加入?随着扫描线的移动,当扫描线会接触到新的线时,需要将其添加到有效边集合中,这时候会产生新的交点,注意此时需要重新排序了
- 扫描线每沿着y轴移动距离deltaY,z就变化k*deltaY

代码实现
【实体类:Edge,用于在边表和有效边集合中存储数据】
package com.dam.entity.sanLine; /** * @Author dam * @create 2023/9/15 14:38 */ public class Edge { public double z; public double yMax; /** * y加一时,z的增量 */ public double k; public Edge(double z, int yMax, double k) { this.z = z; this.yMax = yMax; this.k = k; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
【针对零件点集的纵向扫描线生成方法】
/** * 扫描线生成,使用连贯性算法 * * @param part */ private void vScanLineConstruct1(Part part) { List<Integer> vSLineList = new ArrayList<>(); // 边表 HashMap<Integer, List<Edge>> edgeTable = new HashMap<>(); /* 边表构造 遍历每一条边,将边的信息放入到相应的桶中,即放入边的两点中y值较小的那个桶中 */ for (int i = 0; i < part.offSetOuterContour.size(); i++) { double[] pointI = part.offSetOuterContour.get((i) % part.offSetOuterContour.size()); double[] pointJ = part.offSetOuterContour.get((i + 1) % part.offSetOuterContour.size()); // 两个点中较小的y int yMin = Math.min((int) Math.round(pointI[0]), (int) Math.round(pointJ[0])); int yMax = Math.max((int) Math.round(pointI[0]), (int) Math.round(pointJ[0])); if (yMin == yMax) { // 对于垂直线,不需要添加到边表中 continue; } double z = (int) Math.round(pointI[0]) < (int) Math.round(pointJ[0]) ? pointI[1] : pointJ[1]; Edge edge = new Edge((int) Math.round(z), yMax, MathUtil.getKOfLine(pointI[0], pointI[1], pointJ[0], pointJ[1])); if (!edgeTable.containsKey(yMin)) { List<Edge> edgeList = new ArrayList<>(); edgeList.add(edge); edgeTable.put(yMin, edgeList); } else { edgeTable.get(yMin).add(edge); } } /* 扫描线构造 */ List<Edge> activeEdgeList = new ArrayList<>(); for (int y = 0; y < part.pixelNumInWidDirection; y++) { /// 判断是否有无效边需要移除 int i = 0; while (i < activeEdgeList.size()) { Edge edge = activeEdgeList.get(i); if (edge.yMax == y) { // 当边的yMax==y,该边开始无效,移除边 activeEdgeList.remove(i); } else { i++; } } /// 判断是否有新的有效边加入,如果有的话,需要重新排序 List<Edge> edgeList = edgeTable.get(y); if (edgeList != null && edgeList.size() > 0) { // 需要将新的边添加到有效边集合中 activeEdgeList.addAll(edgeList); // 因为有新边加入,需要重新排序,首先优先按照z的值来升序排序,对于z相同的,按照k升序排序 Collections.sort(activeEdgeList, ((o1, o2) -> { if (o1.z > o2.z) { return 1; } else if (o1.z < o2.z) { return -1; } else { if (o1.k > o2.k) { return 1; } else if (o1.k < o2.k) { return -1; } else { return 0; } } })); } /// 构造扫描线 for (int j = 0; j < activeEdgeList.size(); j += 2) { vSLineList.add(y); vSLineList.add((int)activeEdgeList.get(j).z); vSLineList.add((int)Math.ceil(activeEdgeList.get(j + 1).z)); // 进行增量计算,将z的值增加 activeEdgeList.get(j).z += activeEdgeList.get(j).k; activeEdgeList.get(j + 1).z += activeEdgeList.get(j + 1).k; } } vLineListSort(vSLineList); part.vSLineList = vSLineList; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
当然,这个扫描线生成方法你们并不能直接调用,因为我没有将实体类Part的代码放出来,读者只需要参照上面的思路稍微做一些修改即可,非常简单。除此之外,上面是生成纵线扫描线的方法,生成横线扫描线的方法也类似,举一反三即可
效果测试




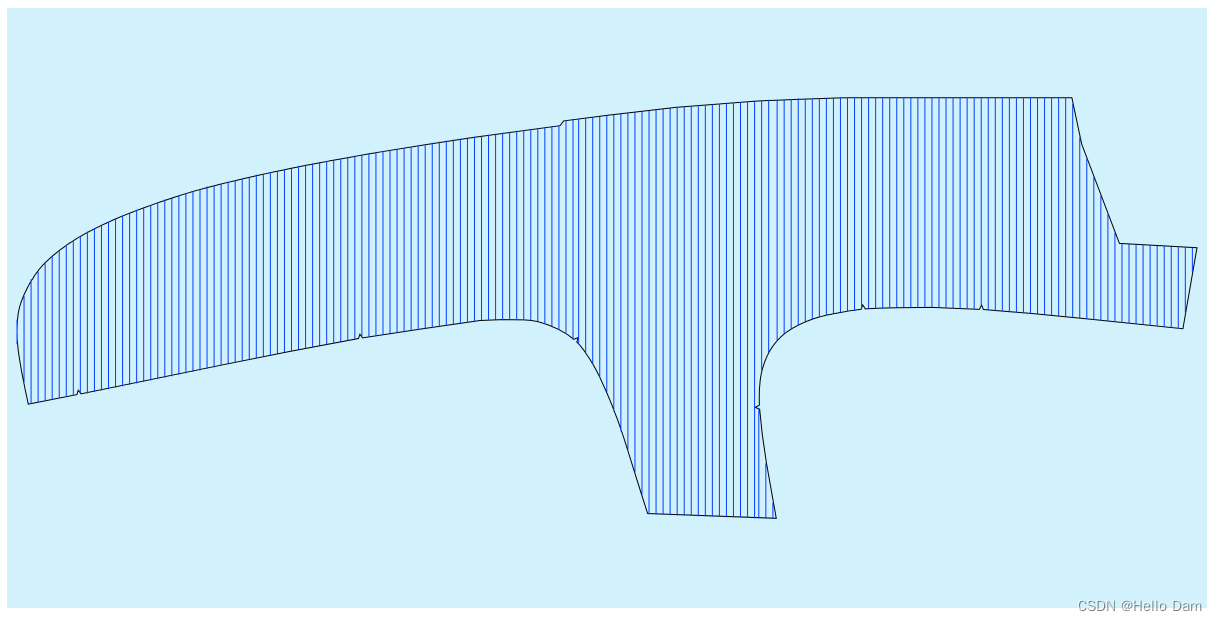

-
相关阅读:
wireguard协议分析
c++面试题汇总-58-118
牛顿插值多项式
day53|1143.最长公共子序列、1035.不相交的线、53. 最大子序和
vulhub中Apache Log4j2 lookup JNDI 注入漏洞(CVE-2021-44228)
云服务器配置Code-Server环境并运行Python和C++
Puppeteer+RabbitMQ:Node.js 批量加工pdf服务架构设计与落地
Java jdbc连接Oracle时出现ORA-28040: No matching authentication protocol报错
2022年了有哪些值得推荐的.NET ORM框架?
周志华机器学习——聚类算法。
- 原文地址:https://blog.csdn.net/laodanqiu/article/details/132912392
